二叉树-------前,中,后序遍历 + 前，中，后序查找+删除节点 （java详解）

news2024/11/27 8:36:00

目录

提要：

 创建一个简单的二叉树：

二叉树的前中后序遍历：

二叉树的前序遍历：

二叉树的中序遍历： 

二叉树的后续遍历：

小结： 

二叉树的前中后续查找：

二叉树的前序查找：

二叉树的中序查找：

二叉树的后续查找: 

代码实现：

二叉树节点删除操作：

思路与约定：

代码实现：

最后，完整代码：

提要：

 二叉树的遍历是指按某条搜索路径访问树中的每个结点，使得每个结点均被访问一次，而且仅能访问一次（说明不可二次访问，一遍而过）。遍历一颗二叉树便要决定对根结点N、左子树L和右子树的访问顺序。 二叉树常的的遍历方法有前序遍历（NLR）、中序遍历（LNR）和后序遍历（LRN）三种遍历算法，其中 “序” 指的是根结点在何时被访问。

遍历大致过程：

前序遍历：根结点 ---> 左子树 ---> 右子树

中序遍历：左子树---> 根结点 ---> 右子树

后序遍历：左子树 ---> 右子树 ---> 根结点

--------------------------------------------------------------------------------------------------------------------------------

 创建一个简单的二叉树：

二叉树的存储结构分为：顺序存储和类似于链表的链式存储，这里我们学习链式存储的方式， 简单枚举一棵二叉树。

用孩子表示法创建一颗二叉树：

//孩子表示法
class KunBinaryTree{
      //数据域
    public int no;//序号
    public String name;//姓名

    public KunBinaryTree left;//左孩子的引用，常常代表左孩子为根的整棵左子树
    public KunBinaryTree right;//右孩子的引用，常常代表右孩子为根的整棵右子树
    //构造方法
    public KunBinaryTree(int no,String name){
        super();
        this.no = no;
        this.name = name;
    }
}
public class TestBinaryTree {
    public static void main(String[] args){
        //对象实例化
        KunBinaryTree root = new KunBinaryTree(1,"唱");
        KunBinaryTree node1 = new KunBinaryTree(2,"跳");
        KunBinaryTree node2 = new KunBinaryTree(3,"rap");
        KunBinaryTree node3 = new KunBinaryTree(4,"篮球");
        KunBinaryTree node4 = new KunBinaryTree(5,"music");
        KunBinaryTree node5 = new KunBinaryTree(6,"坤坤");
    //链接各个节点，使其构成一颗二叉树
        root.left = node1;
        root.right = node2;
        node2.left = node3;
        node2.right = node4;
        node4.left = node5;
    }
}

创建了一颗如图所示的二叉树（一共有6个节点，其中root节点为 “唱”）：

 

-------------------------------------------------------------------------------------------------------------------------------- 

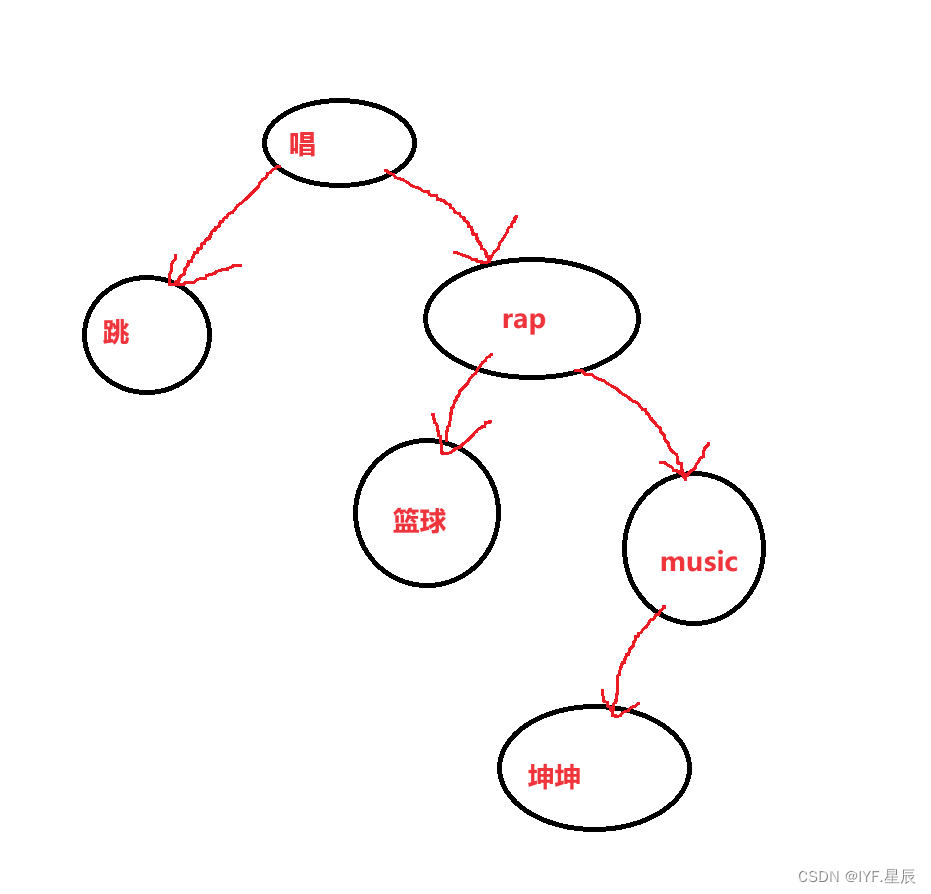
二叉树的前中后序遍历：

通过上面的简单介绍，我们可以开始正式学习接下来的操作了

二叉树的前序遍历：

基本思路：

若二叉树为空，什么都不做，否则：

        i、先访问根结点；

        ii、再前序遍历左子树；

        iii、最后前序遍历右子树；

代码实现：

//前序遍历
    public static void preOrder(KunBinaryTree root){
        if(root == null){
            return ;
        }
        System.out.print(root.no+" "+root.name+" ");//先访问根
        preOrder(root.left);//接着左右子树
        preOrder(root.right);
    }

函数递归展开图解：

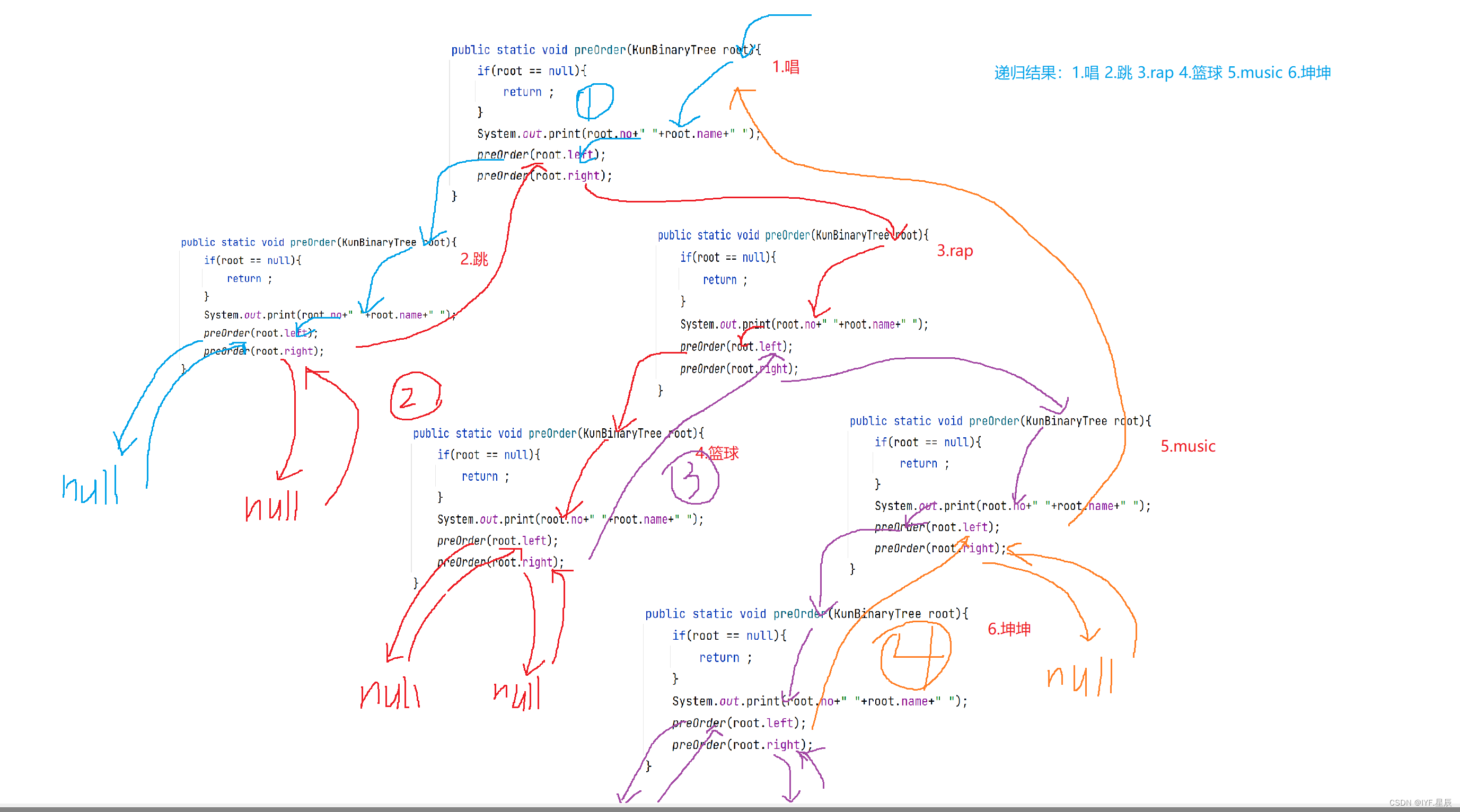
首先，我们从蓝色出发，也就是途中的①，按照先根节点后左右子树的过程进行依次遍历，这里相当于先打印根节点所对应的数据域中的信息后，在接着递归调用左子树，直到为空，回溯后递归调用右子树，直到为空。该树的左子树（总的）调用完后， 开始调用右子树，来到②过程，按照（根-----》左子树---》右子树）的规则继续递归。直到左右子树都为空，返回，也就是③，④过程。从途中可以看出，打印的顺序为：1 唱 2 跳 3 rap 4 篮球 5 music 6 坤坤 

 通过遍历的测试结果也显示，上述过程正确：

 或则用更明了直观的动图解释（图中栗子不为上述栗子，仅做参考，便于理解）：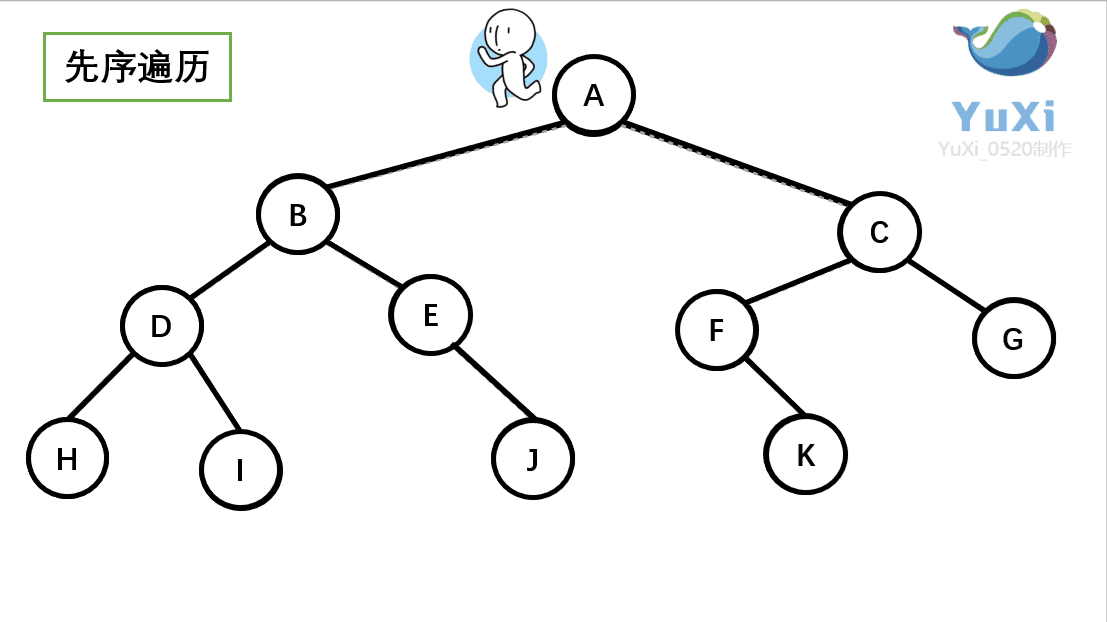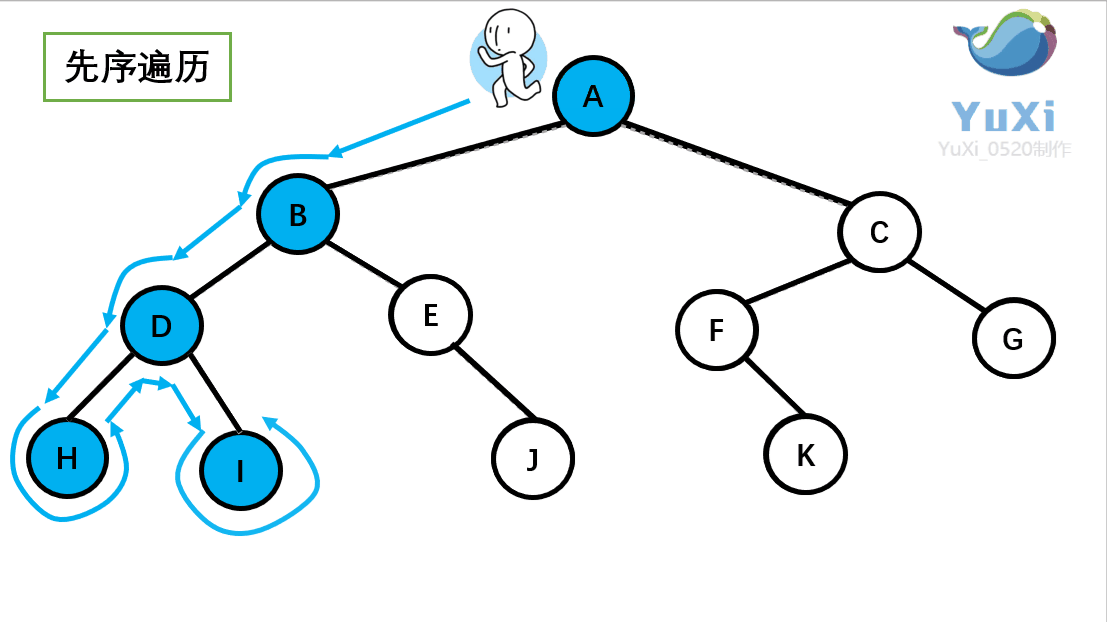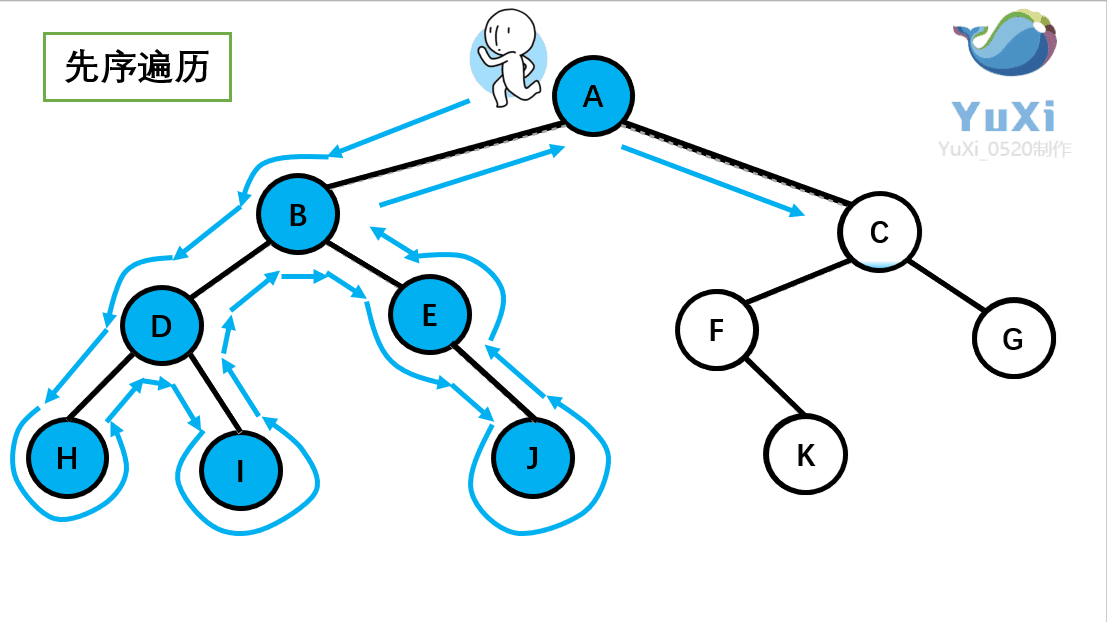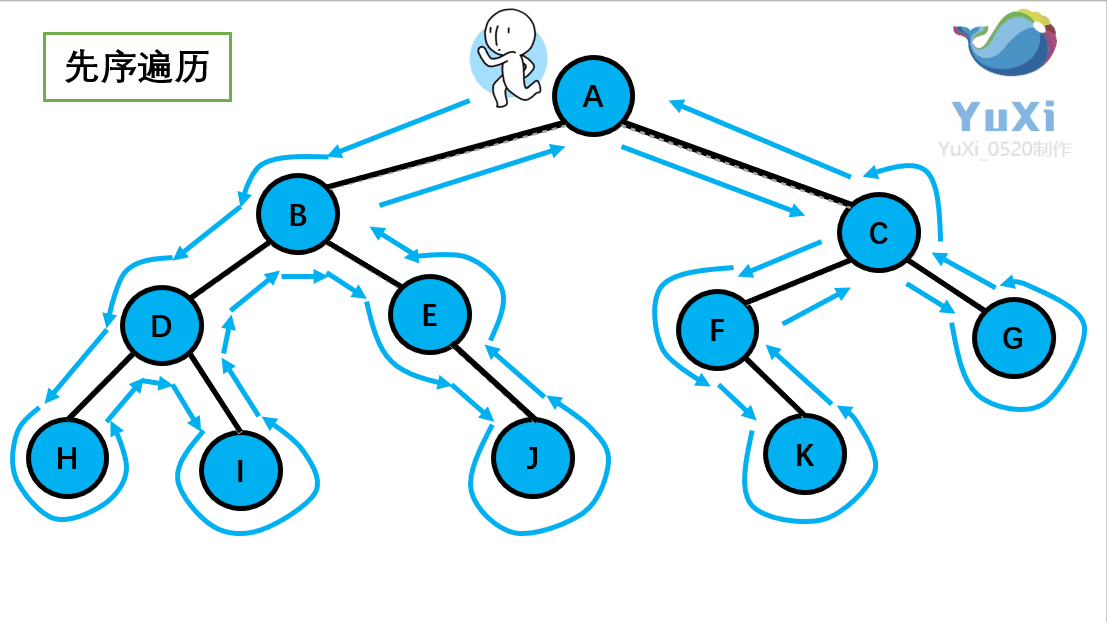

二叉树的中序遍历： 

 基本思路：

二叉树为空，什么也不做，否则：

        i、中序遍历左子树；

        ii、访问根结点；

        iii、中序遍历右子树

代码实现：

 //中序遍历
    public static void infixOrder(KunBinaryTree root){
        if(root == null){
            return ;
        }
        infixOrder(root.left);
        System.out.print(root.no +" "+root.name+" ");
        infixOrder(root.right);
    }

 函数递归展开图：

 首先，我们先从红色出发，也就是①，按照(左子树---》根---》右子树)的规则依次遍历，这里相当于从不可在分割的左子树开始从后往前进行打印输出对应信息，与前序遍历基本一致，就是中间根节点的位置变化导致输出顺序的不同。

最终递归结果为(打印顺序为)：2 跳 1 唱 4 篮球 3 rap 6 坤坤 5 music 

通过测试也可已看出确实是这样:

 用更直观的动图展示（栗子与上述不同，主要是便于理解其过程）：

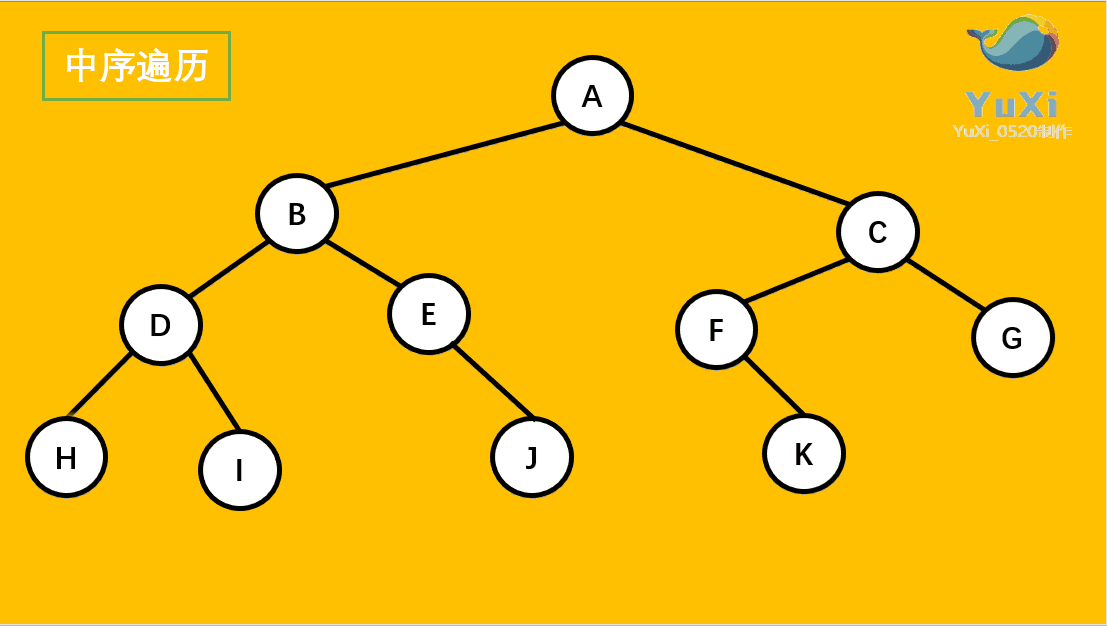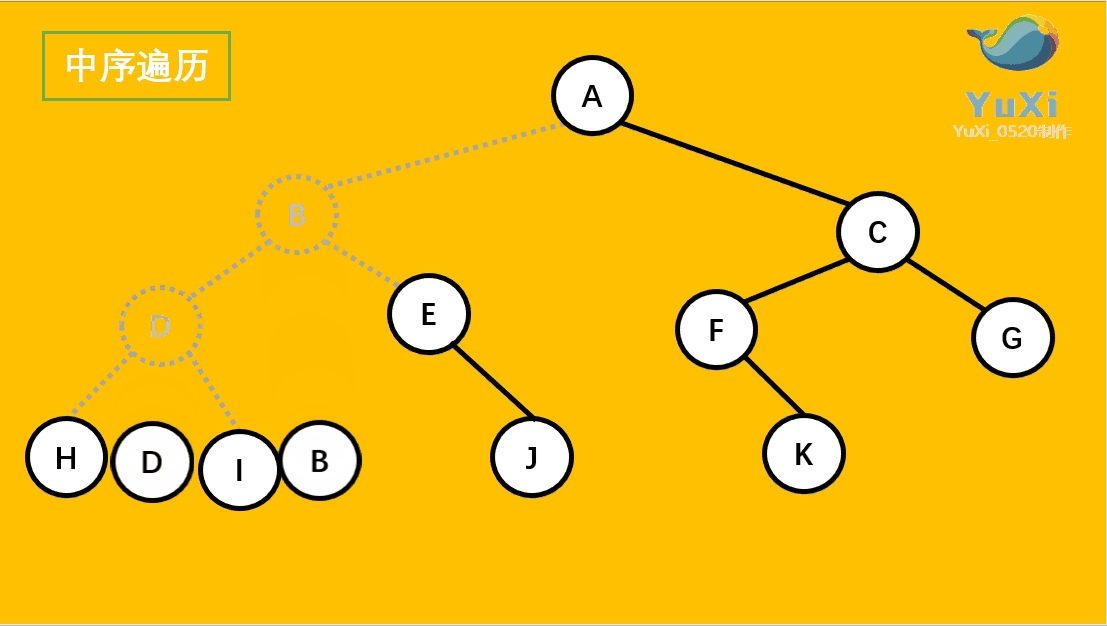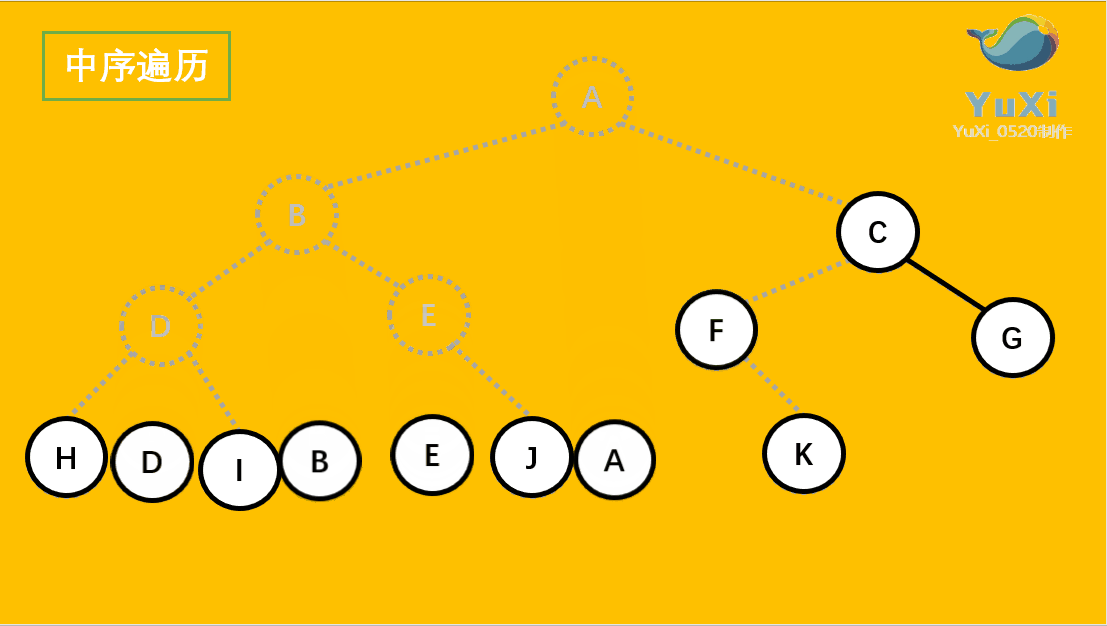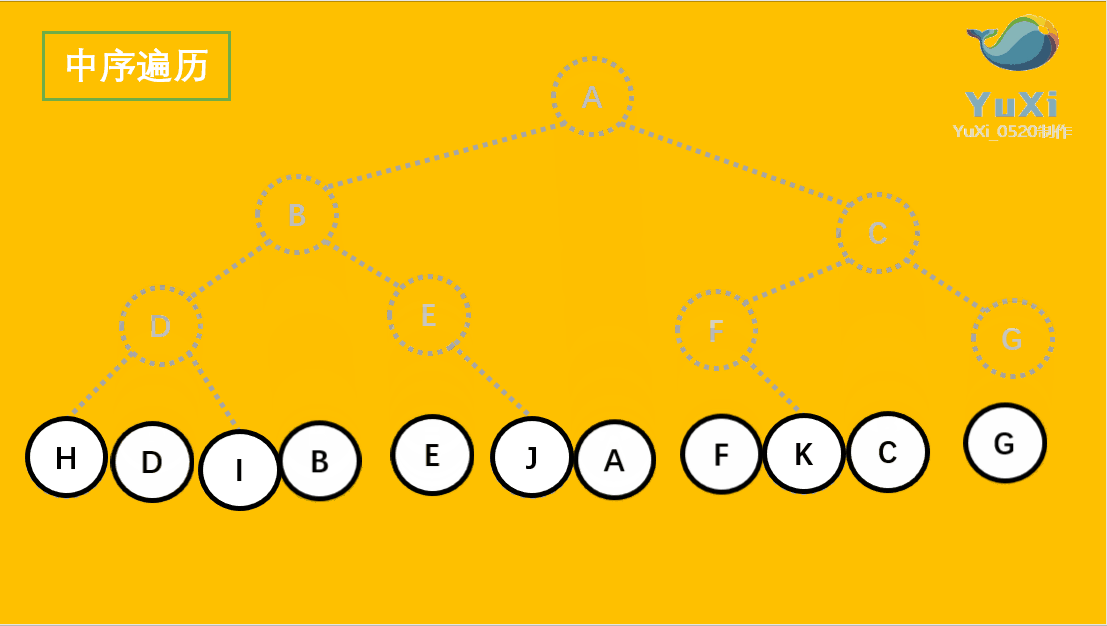
二叉树的后续遍历：

 基本思路：

若二叉树为空，什么也不做，否则：

        i、后序遍历左子树

        ii、后序遍历右子树

        iii、访问根结点

代码实现：

 //后续遍历
    public static void postOrder(KunBinaryTree root){
        if(root == null){
            return ;
        }
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.no +" "+root.name+" ");
    }

 函数递归展开图：

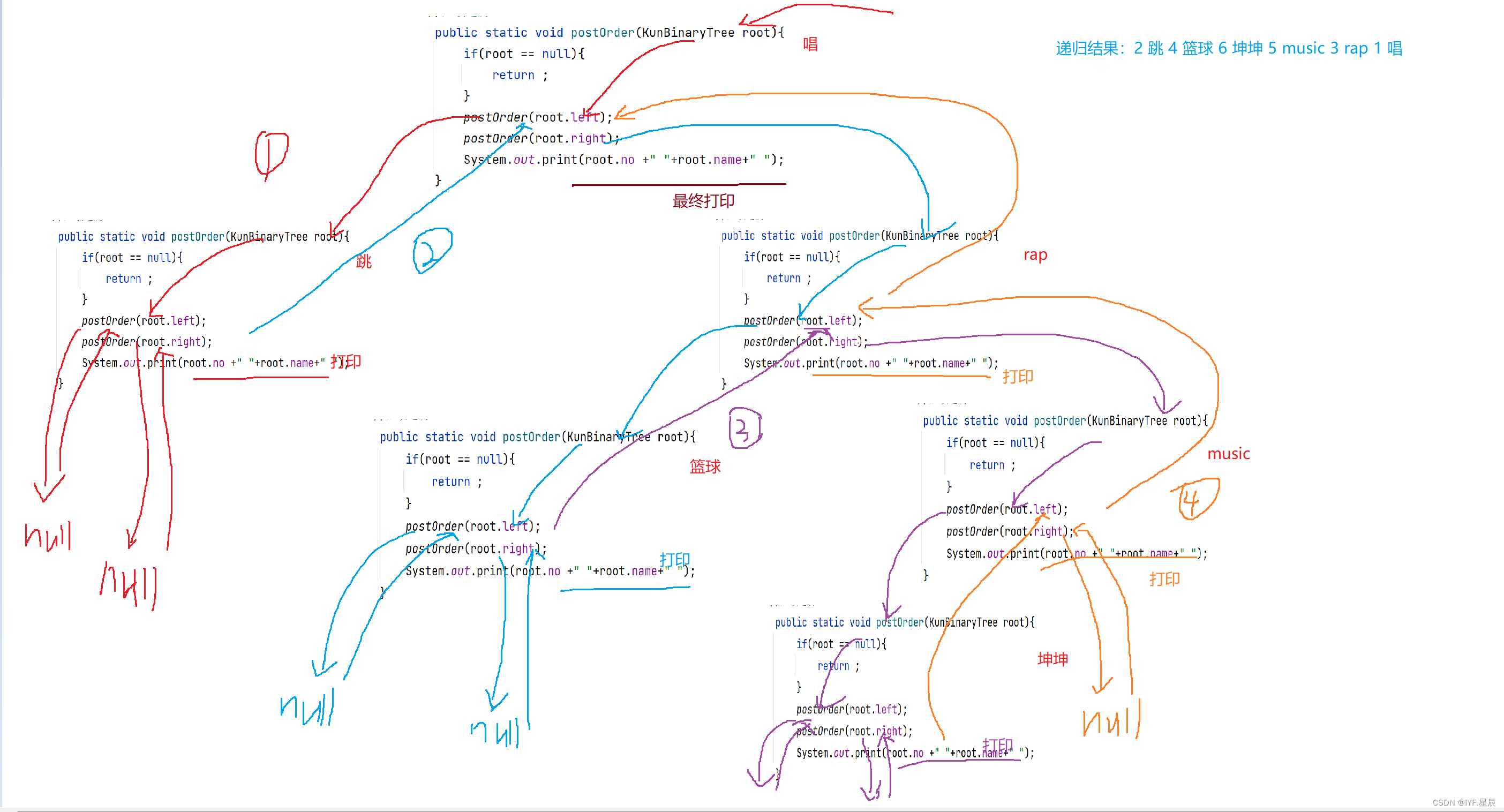
首先从①开始，按照（左子树---》右子树---》根）的规则依次遍历，过程与上述类似，不在赘述。递归结果为:2 跳 4 篮球 6 坤坤 5 music 3 rap 1 唱  

测试结果也表明上述结果正确： 

 用更直观的动图演示该过程（栗子与上述不同，主要是便于理解其过程）：

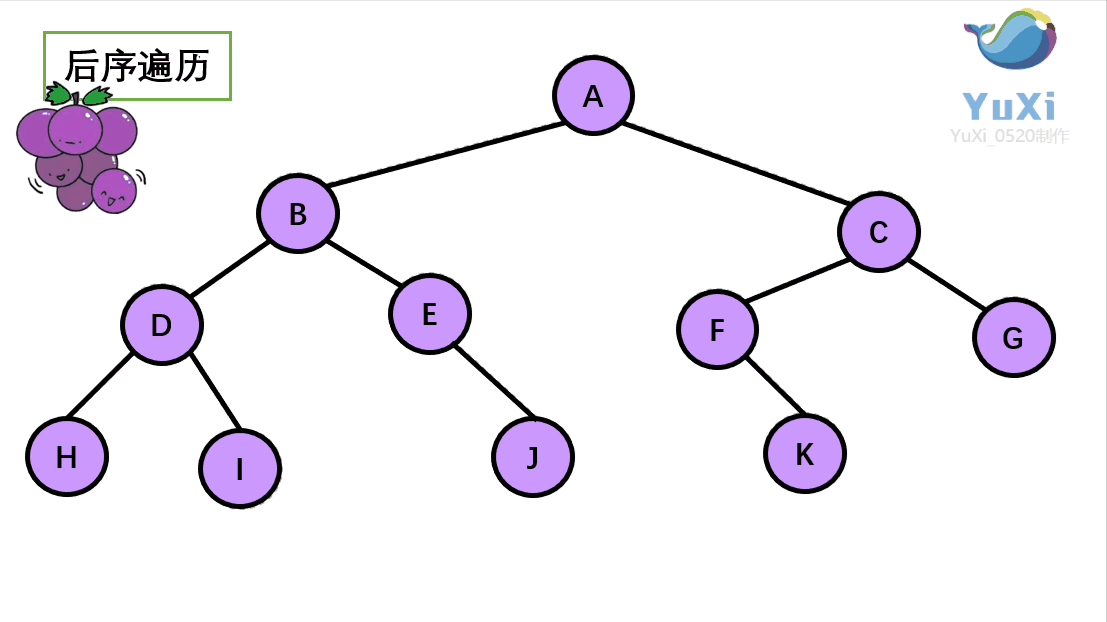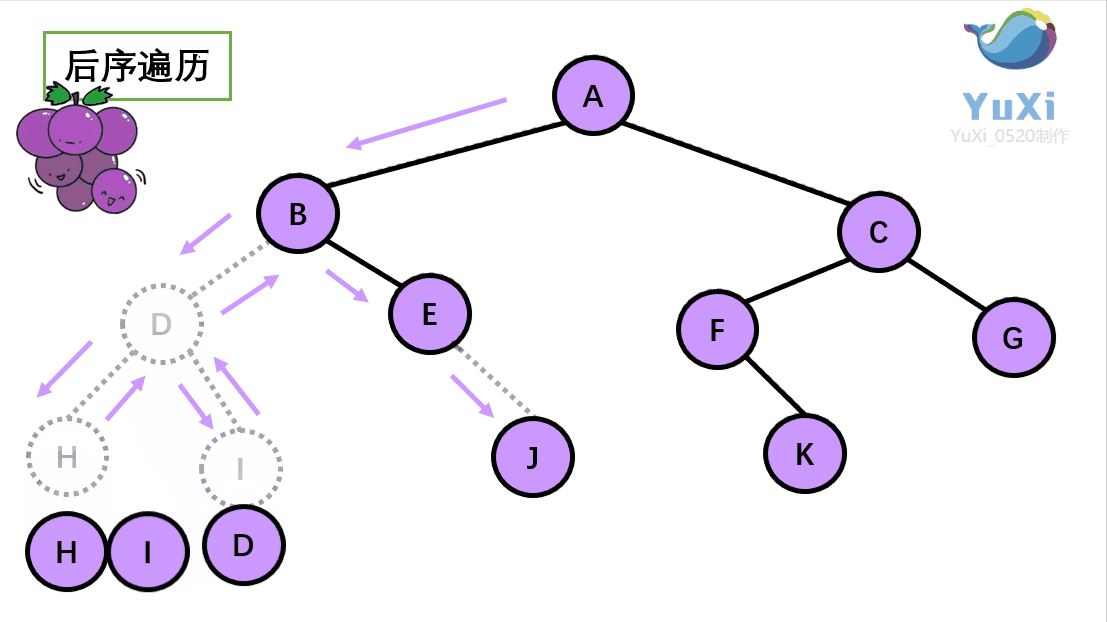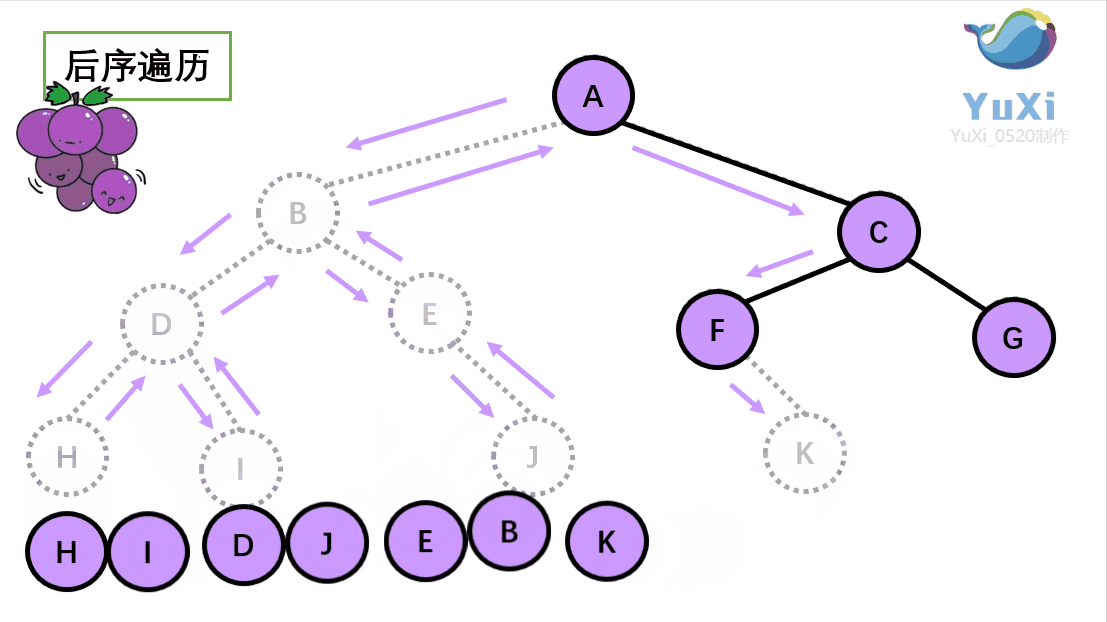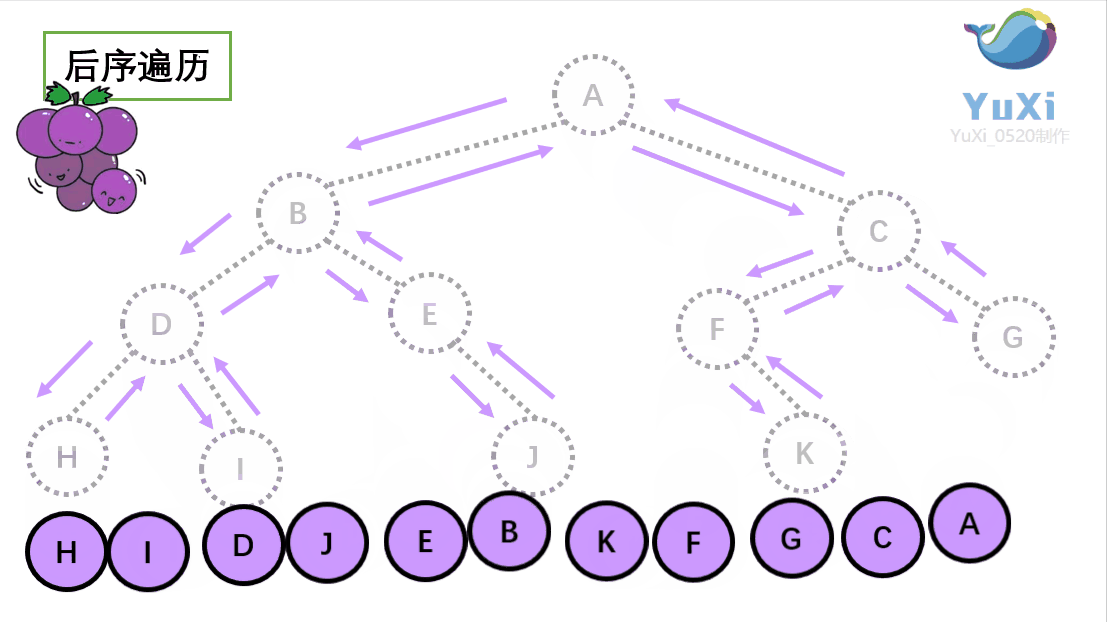
小结： 

比较各个遍历的过程 

前序遍历：根结点 ---> 左子树 ---> 右子树

中序遍历：左子树---> 根结点 ---> 右子树

后序遍历：左子树 ---> 右子树 ---> 根结点

我们不难发现，前序遍历的root节点（栗子中也就是"1.唱"）一定在遍历结果的首部，二中序遍历的root节点在整个树的中部，在遍历的结果中随树的变化二变化，后续遍历的root节点一定在尾部，利用这个特性，我们可以只知道（前序+中序）或者（后续+中序）或则（前序+后续）的遍历结果还原出该二叉树。

二叉树的前中后续查找：

 有了前中后续遍历的实现，我们接着就能实现查找过程，这是基于遍历来实现的

二叉树的前序查找：

基本思路：

1.先判断当前节点的no(序号)是否等于要查找的

2.如果是相等的，则返回当前节点

3.如果不等，则判断当前节点的左右子节点是否为空，如果不为空，则递归前序查找

4.如果左递归前序查找找到节点，则返回，否则继续判断当前节点的左右子节点是否为空，如果不为空，则继续右递归前序查找

代码实现：

//前序查找
    public static int count1 = 0;//用于记录递归查找的次数
    public static KunBinaryTree preOrderSearch(KunBinaryTree root,int no){
        ++count1;
        if(root.no == no){
            return root;
        }

        KunBinaryTree resNode = null;
        if(root.left != null){
            resNode = preOrderSearch(root.left,no);
        }
        if(resNode != null){
            return resNode;
        }
        if(root.right != null){
            resNode = preOrderSearch(root.right,no);
        }
        return resNode;
    }

按照上述的遍历结果我们可以知道，一共进行了6次遍历，（咱们这里查找数字6）那么前序查找遍历的次数为6（即count1=6）：

测试结果：

 

二叉树的中序查找：

 基本思路：

1.判断当前节点的左右子节点是否为空，如果不为空，则递归中序查找

2.如果找到，则返回，若果没有找到，就和当前节点比较，如果是则返回当前节点，否则继续进行右递归的中序查找

3.右递归中序查找，找到就返回，否则返回null

代码实现：

//中序查找
    public static int count2 = 0;//记录中序查找次数
    public static KunBinaryTree infixOrderSearch(KunBinaryTree root,int no){
        KunBinaryTree resNode = null;
        if(root.left != null){
            resNode = infixOrderSearch(root.left,no);
        }
        if(resNode != null){
            return resNode;
        }
   ++count2;
        if(root.no == no){
            return root;
        }

        if(root.right != null){
            resNode = infixOrderSearch(root.right,no);
        }
        return resNode;
    }

按照上述的遍历结果我们可以知道，一共进行了6次遍历，（咱们这里查找数字6）那么中序查找的遍历次数为5（count2=5）:

测试结果：

二叉树的后续查找: 

 基本思路：

1.判断当前节点的左子节点是否为空，如果不为空，则递归后序查找

2.如果找到，就返回，如果没有找到，就判断当前节点的有子节点是否为空，如果不为空，则右递归进行后序查找，如果找到，就返回

3.接着和当前节点进行比较，找到则返回，否则返回null

代码实现：

   //后序查找
    public static int count3 = 0;//记录后序查找遍历次数
    public static KunBinaryTree postOrderSearch(KunBinaryTree root,int no){
        KunBinaryTree resNode = null;
        if(root.left != null){
            resNode = postOrderSearch(root.left,no);
        }
        if(resNode != null){
            return resNode;
        }

        if(root.right != null){
            resNode = postOrderSearch(root.right,no);
        }
        if(resNode != null){
            return resNode;
        }
        ++count3;
        if(root.no == no){
            return root;
        }
        return resNode;
    }

按照上述的遍历结果我们可以知道，一共进行了6次遍历，（咱们这里查找数字6）那么后序查找的次数为3（count3=3）:

测试结果：

 

二叉树节点删除操作：

 最后，咱么来进行二叉树节点删除的操作

思路与约定：

代码实现：

 //删除节点
    public static void delTreeNode(KunBinaryTree root,int no){
        if(root.no == no){
            root = null;
        }else{
            if(root.left != null && root.left.no == no){
                root.left = null;
                return ;
            }
            if(root.right != null && root.right.no == no){
                root.right = null;
                return ;
            }
            if(root.left != null){
                delTreeNode(root.left,no);
            }
            if(root.right != null){
                delTreeNode(root.right,no);
            }
        }
    }

 

这里我们删除4子节点，也就是篮球 

测试结果：

当我们删除3这个子节点时，后面的节点也一并删除了：

 

最后，完整代码：

import java.util.*;

class KunBinaryTree{
    public int no;
    public String name;
    public KunBinaryTree left;
    public KunBinaryTree right;
    public KunBinaryTree(int no,String name){
        super();
        this.no = no;
        this.name = name;
    }
}

public class BinaryTree {
//前中后序遍历
    //前序遍历
    public static void preOrder(KunBinaryTree root){
        if(root == null){
            return ;
        }
        System.out.print(root.no+" "+root.name+" ");
        preOrder(root.left);
        preOrder(root.right);
    }
   //中序遍历
    public static void infixOrder(KunBinaryTree root){
        if(root == null){
            return ;
        }
        infixOrder(root.left);
        System.out.print(root.no +" "+root.name+" ");
        infixOrder(root.right);
    }
   //后续遍历
    public static void postOrder(KunBinaryTree root){
        if(root == null){
            return ;
        }
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.no +" "+root.name+" ");
    }
//前中后序查找
    //前序查找
    public static int count1 = 0;//用于记录递归查找的次数
    public static KunBinaryTree preOrderSearch(KunBinaryTree root,int no){
        ++count1;
        if(root.no == no){
            return root;
        }

        KunBinaryTree resNode = null;
        if(root.left != null){
            resNode = preOrderSearch(root.left,no);
        }
        if(resNode != null){
            return resNode;
        }
        if(root.right != null){
            resNode = preOrderSearch(root.right,no);
        }
        return resNode;
    }
    //中序查找
    public static int count2 = 0;//记录中序查找次数
    public static KunBinaryTree infixOrderSearch(KunBinaryTree root,int no){
        KunBinaryTree resNode = null;
        if(root.left != null){
            resNode = infixOrderSearch(root.left,no);
        }
        if(resNode != null){
            return resNode;
        }
   ++count2;
        if(root.no == no){
            return root;
        }

        if(root.right != null){
            resNode = infixOrderSearch(root.right,no);
        }
        return resNode;
    }

   //后序查找
    public static int count3 = 0;//记录后序查找遍历次数
    public static KunBinaryTree postOrderSearch(KunBinaryTree root,int no){
        KunBinaryTree resNode = null;
        if(root.left != null){
            resNode = postOrderSearch(root.left,no);
        }
        if(resNode != null){
            return resNode;
        }

        if(root.right != null){
            resNode = postOrderSearch(root.right,no);
        }
        if(resNode != null){
            return resNode;
        }
        ++count3;
        if(root.no == no){
            return root;
        }
        return resNode;
    }
    //删除节点
    public static void delTreeNode(KunBinaryTree root,int no){
        if(root.no == no){
            root = null;
        }else{
            if(root.left != null && root.left.no == no){
                root.left = null;
                return ;
            }
            if(root.right != null && root.right.no == no){
                root.right = null;
                return ;
            }
            if(root.left != null){
                delTreeNode(root.left,no);
            }
            if(root.right != null){
                delTreeNode(root.right,no);
            }
        }
    }
    //测试
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);

        KunBinaryTree root = new KunBinaryTree(1,"唱");
        KunBinaryTree node1 = new KunBinaryTree(2,"跳");
        KunBinaryTree node2 = new KunBinaryTree(3,"rap");
        KunBinaryTree node3 = new KunBinaryTree(4,"篮球");
        KunBinaryTree node4 = new KunBinaryTree(5,"music");
        KunBinaryTree node5 = new KunBinaryTree(6,"坤坤");

        root.left = node1;
        root.right = node2;
        node2.left = node3;
        node2.right = node4;
        node4.left = node5;

        preOrder(root);
        System.out.println();

        infixOrder(root);
        System.out.println();
        postOrder(root);
        System.out.println();

        System.out.print("请输入要查找的数字：");
        int n = sc.nextInt();
        KunBinaryTree resNode = postOrderSearch(root,n);
        System.out.println("一共查找的次数count3："+count3);
        if(resNode != null){
            System.out.printf("找到了,Kun节点 no=%d name=%s",resNode.no,resNode.name);
        }else{
            System.out.printf("没有找到Kun节点%d的信息",n);
        }
        System.out.println();
        System.out.print("请输入要删除的子节点：");
        int n2 = sc.nextInt();
        System.out.println("删除前：");
        preOrder(root);
        System.out.println();
        System.out.println("删除后：");
        delTreeNode(root,n2);
        preOrder(root);

    }
}

博客到这里也是结束了，制作不易，喜欢的小伙伴可以点赞加关注支持下博主，这对我真的很重要~~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1448751.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

面试前的准备

面试前的准备

面试前的准备 Java程序员校招与社招的区别 校招和社招都是企业招聘形式的一种，只是面向的对象不同。校招 只允许在校生参加，社招理论上是任何人都能参加的(包括在校生)。 但是，无论是社招还是校招，它的难度都取决于你的水平高低。…
阅读更多...
VueCLI核心知识4：动画效果、过渡效果

VueCLI核心知识4：动画效果、过渡效果

1 动画效果 【代码】 <template><div><button click"isShow !isShow">显示/隐藏</button><!-- <transition name"xxx" :appear"true"> 可以指定name属性&#xff0c;也可以不指定&#xff0c;name属性在有…
阅读更多...
红日靶场2学习

红日靶场2学习

靶场下载来自&#xff1a; http://vulnstack.qiyuanxuetang.net/vuln/detail/3/ 靶场统一登录密码&#xff1a;1qazWSX 按大佬的说法是 环境需要模拟内网和外网两个网段&#xff0c;PC端虚拟机相当于网关服务器&#xff0c;所以需要两张网卡&#xff0c;一个用来向外网提供web…
阅读更多...
Django学习全纪录：编写你的第一个 Django 应用，Django内置数据库的配置，以及扩展性的数据库介绍和配置

Django学习全纪录：编写你的第一个 Django 应用，Django内置数据库的配置，以及扩展性的数据库介绍和配置

天下古今之庸人&#xff0c;皆以一惰字致败&#xff1b;天下古今之人才&#xff0c;皆以一傲字致败。——[清]曾国藩 导言 大家好&#xff0c;在上一篇文章里&#xff0c;我们一起学习了Django的视图以及路由&#xff0c;并且对Django的应用有了初步的认识&#xff0c;掌握了…
阅读更多...
DS:二叉树的链式结构及实现

DS:二叉树的链式结构及实现

创作不易&#xff0c;友友们给个三连吧&#xff01;&#xff01; 一、前言 前期我们解释过二叉树的顺序结构&#xff08;堆&#xff09;为什么比较适用于完全二叉树&#xff0c;因为如果用数组来实现非完全二叉树&#xff0c;那么数组的中间部分就可能会存在大量的空间浪费。 …
阅读更多...
JVM（3）高级篇

JVM（3）高级篇

1 GraalVM 1.1 什么是GraalVM GraalVM是Oracle官方推出的一款高性能JDK&#xff0c;使用它享受比OpenJDK或者OracleJDK更好的性能。 GraalVM的官方网址&#xff1a;https://www.graalvm.org/ 官方标语&#xff1a;Build faster, smaller, leaner applications。 更低的CPU、内…
阅读更多...
vivim复习

vivim复习

vi/vim常用命令 vi&vim常用命令 set nu 显示行号 gg 跳转到文件开头 / 向后搜索 ? 向前搜索 n 查找下一处N 查找上一处 | 光标所在行行首L 屏幕所显示的底行{ 段首} 段尾- 前一行行首 后一行行首 ( 句首 ) 下一句首 $ 行末 M 屏…
阅读更多...
Javaweb基础-tomcat，servlet

Javaweb基础-tomcat，servlet

一.配置文件基础&#xff1a; properties配置文件&#xff1a; 由键值对组成 键和值之间的符号是等号 每一行都必须顶格写&#xff0c;前面不能有空格之类的其他符号 xml配置文件&#xff1a;&#xff08;xml语法HTML语法HTML约束&#xff09;xml约束-DTD / Schema DOM4…
阅读更多...
单测的思路

单测的思路

文章目录 单测的定义方法的单测几种生成工具的对比生成步骤 接口的单测场景的单测总结参考 单测的定义 单元测试&#xff08;Unit Testing&#xff09;是一种软件开发中的测试方法&#xff0c;它的主要目的是确保软件中的最小可测试单元&#xff08;通常是函数、方法或类&…
阅读更多...
今日arXiv最热NLP大模型论文：清华提出LongAlign，打破长上下文对齐瓶颈，数据、训练策略、评估基准一网打尽

今日arXiv最热NLP大模型论文：清华提出LongAlign，打破长上下文对齐瓶颈，数据、训练策略、评估基准一网打尽

随着LLMs的发展&#xff0c;其支持的上下文长度越来越长。仅一年时间&#xff0c;GPT-4就从一开始的4K、8K拓展到了128k。 128k什么概念&#xff1f;相当于一本300页厚的书。这是当初只支持512个tokens的BERT时代不敢想象的事情。 随着上下文窗口长度的增加&#xff0c;可以提…
阅读更多...
【STM32 CubeMX】GPIO的工作模式

【STM32 CubeMX】GPIO的工作模式

文章目录 前言一、有哪些工作模式&#xff1f;1.1 GPIO的详细介绍1.2 GPIO的内部框图输入模式输出部分 总结 前言 在嵌入式系统开发中&#xff0c;对于STM32微控制器的GPIO&#xff08;General Purpose Input/Output&#xff09;引脚的配置和使用是至关重要的。GPIO引脚可以通…
阅读更多...
MySQL 基础知识（六）之数据查询（一）

MySQL 基础知识（六）之数据查询（一）

目录 1 基本查询 1.1 查询相关列 (select * / 列名) 1.2 别名 (as) 1.3 去重 (distinct) 1.4 对列中的数据进行运算 (、-、*、/) 2 条件查询 (where) 2.1 等值查询 () 2.2 非等值查询 (>、<、>、<、!、><) 2.3 逻辑判断 (and、or、not) 2.4 区间判…
阅读更多...
累加器 - 分布式共享写变量

累加器 - 分布式共享写变量

水善利万物而不争&#xff0c;处众人之所恶&#xff0c;故几于道&#x1f4a6; 文章目录 概念注意&#xff1a;应用 概念 因为RDD是可分区的&#xff0c;每个分区在不同的节点上运行&#xff0c;如果想要对某个值进行全局累加&#xff0c;就需要将每个task中的值取到然后进行累…
阅读更多...
【Linux笔记】进程间通信之管道

【Linux笔记】进程间通信之管道

一、匿名管道 我们在之前学习进程的时候就知道了一个概念&#xff0c;就是进程间是互相独立的&#xff0c;所以就算是两个进程是父子关系&#xff0c;其中一个进程退出了也不会影响另一个进程。 也因为进程间是互相独立的&#xff0c;所以两个进程间就不能直接的传递信息或者…
阅读更多...
C++ 特殊类的实现

C++ 特殊类的实现

一、请设计一个类&#xff0c;不能被拷贝 拷贝只会放生在两个场景中&#xff1a;拷贝构造函数以及赋值运算符重载&#xff0c;因此想要让一个类禁止拷贝&#xff0c;只需让该类不能调用拷贝构造函数以及赋值运算符重载即可。 在C98中&#xff1a;将拷贝构造函数与赋值运算符重载…
阅读更多...
【Java记】数据类型与变量

【Java记】数据类型与变量

一、数据类型 在Java中数据类型主要分为两类&#xff1a;基本数据类型和引用数据类型。基本数据类型有四类八种&#xff1a; 四类&#xff1a;整型、浮点型、字符型以及布尔型八种&#xff1a; 数据类型 关键字 内存占用 范围 字节型 byte 1 字节 -128~ 127 短整型 …
阅读更多...
【C语言】数据结构#实现堆

【C语言】数据结构#实现堆

目录 &#xff08;一&#xff09;堆 &#xff08;1&#xff09;堆区与数据结构的堆 &#xff08;二&#xff09;头文件 &#xff08;三&#xff09;功能实现 &#xff08;1&#xff09;堆的初始化 &#xff08;2&#xff09;堆的销毁 &#xff08;3&#xff09;插入数据 …
阅读更多...
Vue3+Vite+TS+Pinia+ElementPlus+Router+Axios创建项目

Vue3+Vite+TS+Pinia+ElementPlus+Router+Axios创建项目

目录 初始项目组成1. 创建项目1.1 下载项目依赖1.2 项目自动启动1.3 src 别名设置vite.config.ts配置文件tsconfig.json配置若新创项目ts提示1.4 运行测试2. 清除默认样式2.1 样式清除代码下载2.2 src下创建公共样式文件夹`style`2.3 main.js中引入样式2.4 安装`sass`解析插件2…
阅读更多...
SpringCloud之Eureka注册中心和负载均衡

SpringCloud之Eureka注册中心和负载均衡

SpringCloud之Eureka注册中心和负载均衡 微服务技术栈认识微服务单体架构分布式架构微服务 微服务拆分及远程调用微服务拆分注意事项 Eureka注册中心提供者与消费者原理分析服务调用出现的问题Eureka的作用 使用流程1、搭建EurekaServer2、注册user-service3、在order-service完…
阅读更多...
代码随想录算法训练营第三十一天 |基础知识，455.分发饼干，376.摆动序列，53.最大子序和（已补充）

代码随想录算法训练营第三十一天 |基础知识，455.分发饼干，376.摆动序列，53.最大子序和（已补充）

基础知识&#xff1a; 题目分类大纲如下&#xff1a; #算法公开课 《代码随想录》算法视频公开课(opens new window)&#xff1a;贪心算法理论基础&#xff01;(opens new window),相信结合视频再看本篇题解&#xff0c;更有助于大家对本题的理解。 #什么是贪心 贪心的本质…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023