先来回顾一下笛卡尔树的性质:笛卡尔树是这样一个二叉树,它能保持原序列的先后顺序,并且具备堆的性质。这里假设序列中无相等元素。
假设有一个序列{9,3,7,1,8,12,10,20,15,18,5},以此序列来建立一个笛卡尔树,则建好后的二叉树,中序访问该二叉树仍会得到原来的序列{9,3,7,1,8,12,10,20,15,18,5},且该二叉树还是一个堆(大根堆或小根堆)。以小根堆为例,则建成的笛卡尔树如图所示:
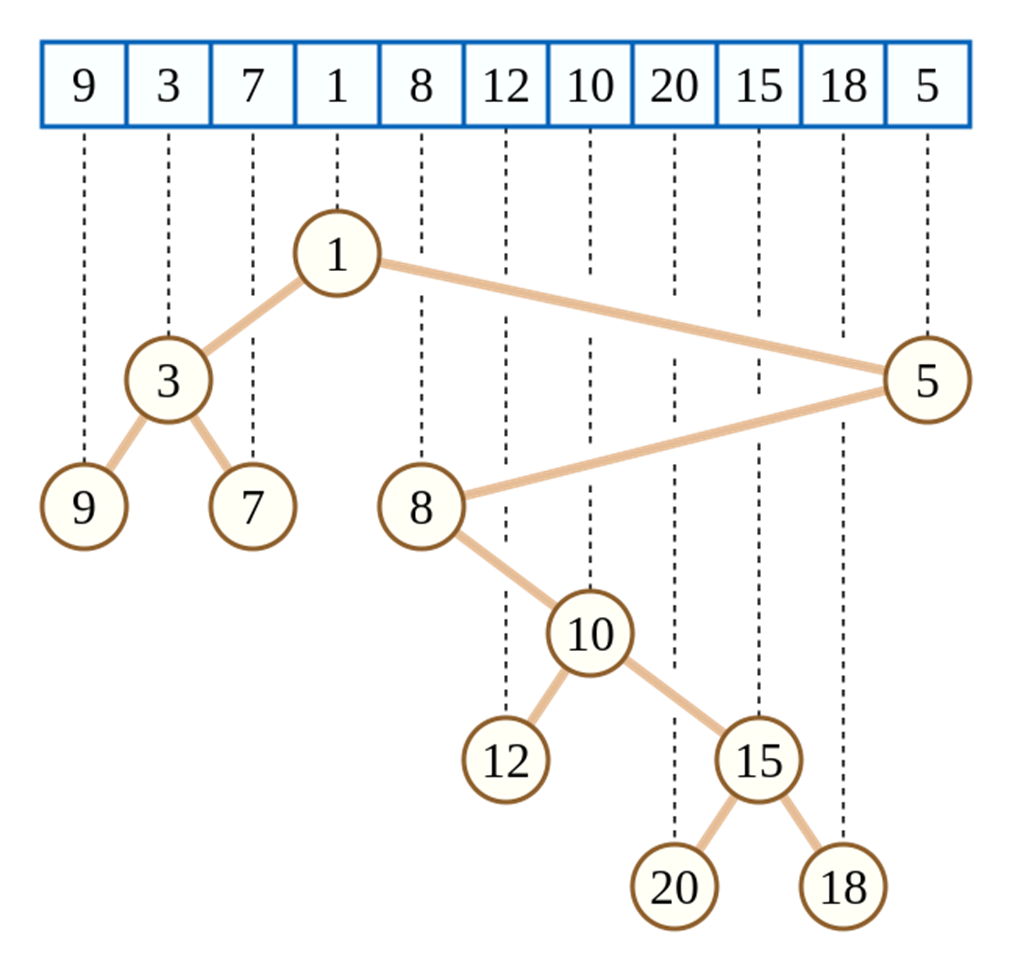
图源自维基百科
来说一下根据指定序列,建立笛卡尔树的思路:
因为新加入的节点在顺序上排在后面,所以只能在树的“右链”中寻找新节点应该插入的位置。(对右链操作的详细解释,可以看https://oi-wiki.org/ds/cartesian-tree/)那么怎么找到合适的位置?最简单的情况:新的节点的值大于右链中的叶子节点(设右链有k个节点),将新节点直接接到右链的右端,作为右链新的叶子节点即可,因为,加入该节点后,并没有破坏原来小根堆的性质。
更为复杂的情况:新的节点的值要比右链中的值新的节点的值()
中的至少一个值小。那么,我们需要找到在右链中的合适位置,使得
此时,为了保持小根堆的性质,我们需要在原先节点的位置插入新节点,另成为的右子树,原先节点则成为新节点的左子树。这样,既保证了小根堆的性质,又使新节点永远是右链中最末端(叶子)节点。
还有一种特殊情况,即
此时新节点成为根节点,移动到的左子树。即右链只有一个节点。
观察整个插入过程,只会牵扯到右链中的节点,非右链节点不会变动位置。每次从右链的末端到根部进行遍历,找到合适的位置插入新节点,并把值更大的节点调整到新节点的左子树中。
可以用一个栈来保存右链信息。每次插入新节点,从栈顶一个个比较,比新节点值大的节点弹出,直到找到合适位置。弹出的最后一个节点作为新节点的左子树。新节点作为栈中上一个节点(如果有)的右子树。
代码如下所示。此处用数组来实现的栈,并没有真的做弹出操作,而只是更新了栈顶元素的位置,记录栈顶元素下标的变量top- - 即模拟栈弹出操作。
完成笛卡尔树的遍历后,中序遍历该树,仍保持原序列顺序。
代码如下所示:
#include<iostream>
using namespace std;
struct TreeNode {
int value;
struct TreeNode* leftChild;
struct TreeNode* rightChild;
};
void midOrderVisit(TreeNode *tnd) {
if (tnd==nullptr)
return;
midOrderVisit(tnd->leftChild);
cout << tnd->value << endl;
midOrderVisit(tnd->rightChild);
}
int main() {
int n;
cout << "输入数组个数n" << endl;
cin >> n;
int* a = (int*)malloc(n * sizeof(int));
for (int i = 0; i < n; i++) {
cin >> a[i];
}
TreeNode** stk = (TreeNode**)malloc(n * sizeof(TreeNode*));
TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
root->value = a[0];
root->leftChild = NULL;
root->rightChild = NULL;
stk[0] = root;
int top = 0;
for (int i = 1; i < n; i++) {
TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));
newNode->value = a[i];
newNode->leftChild = NULL;
newNode->rightChild = NULL;
int flag;
flag = 0;
while (top >= 0 && newNode->value < stk[top]->value) {
top--;
flag = 1;
}
if (flag) {
newNode->leftChild = stk[top+1];
}
top++;
stk[top] = newNode; //入栈
if (top >= 1) {
stk[top - 1]->rightChild = newNode;
}
}
//中序遍历树
midOrderVisit(stk[0]);
return 0;
}