一、图示展示：

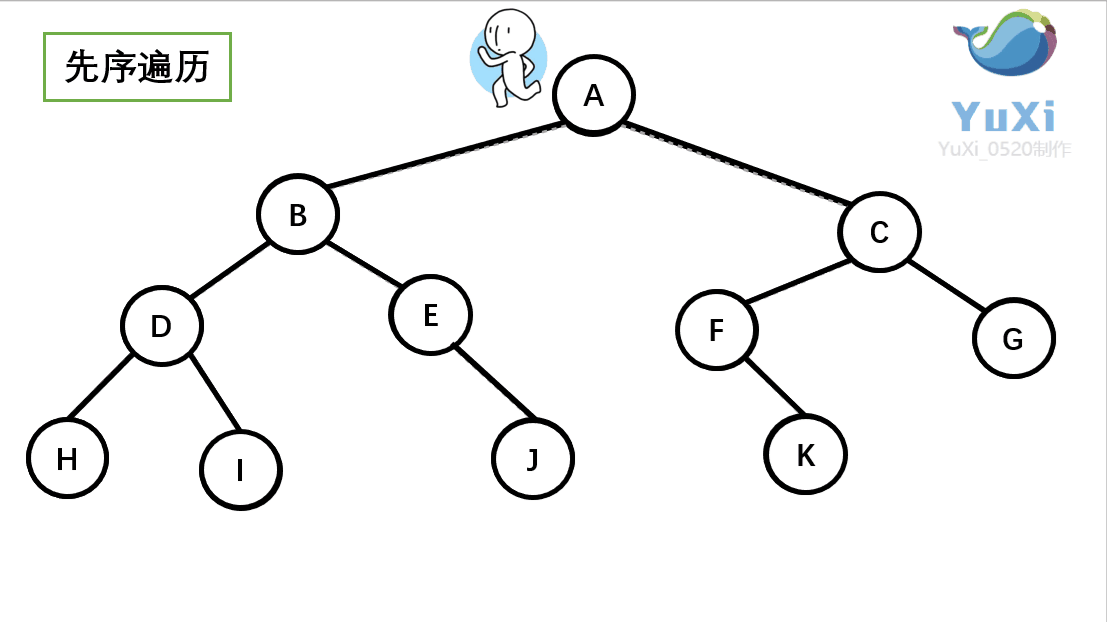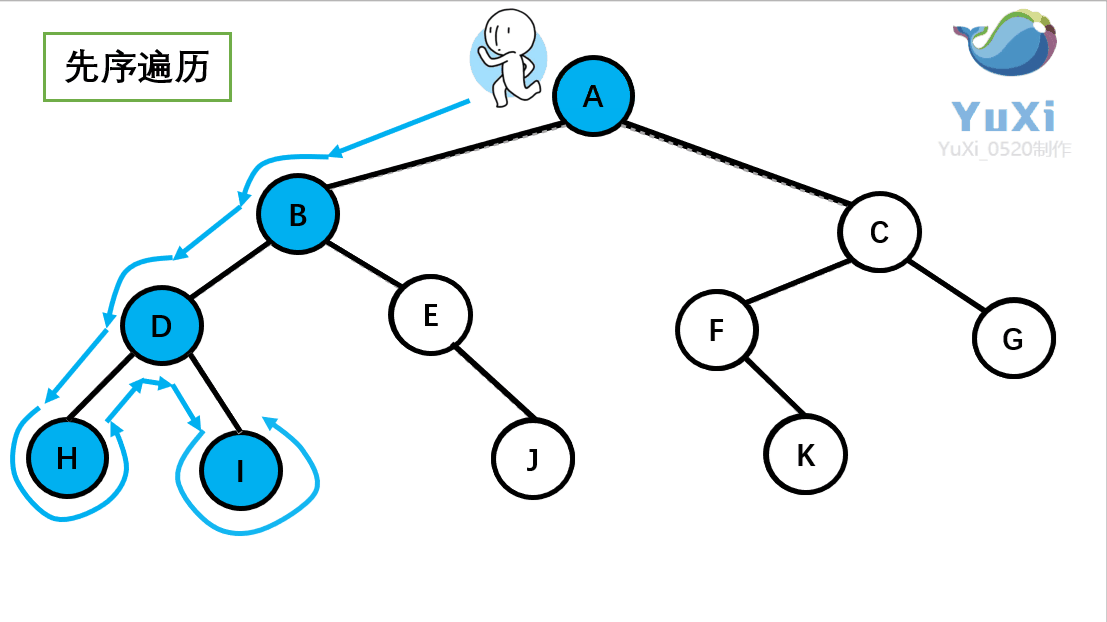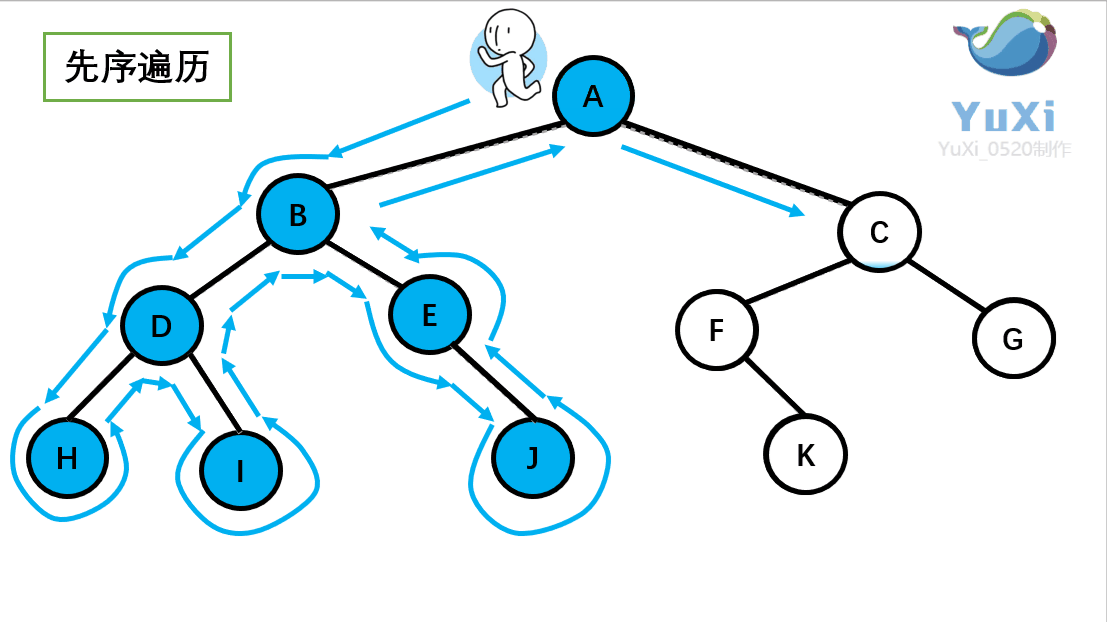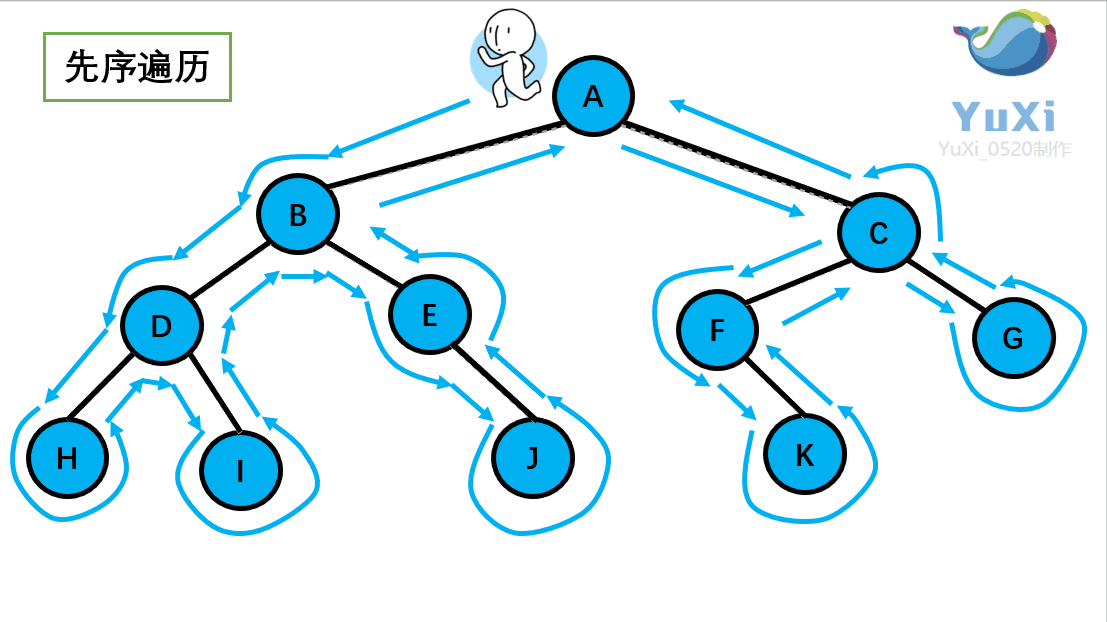
（1）先序遍历

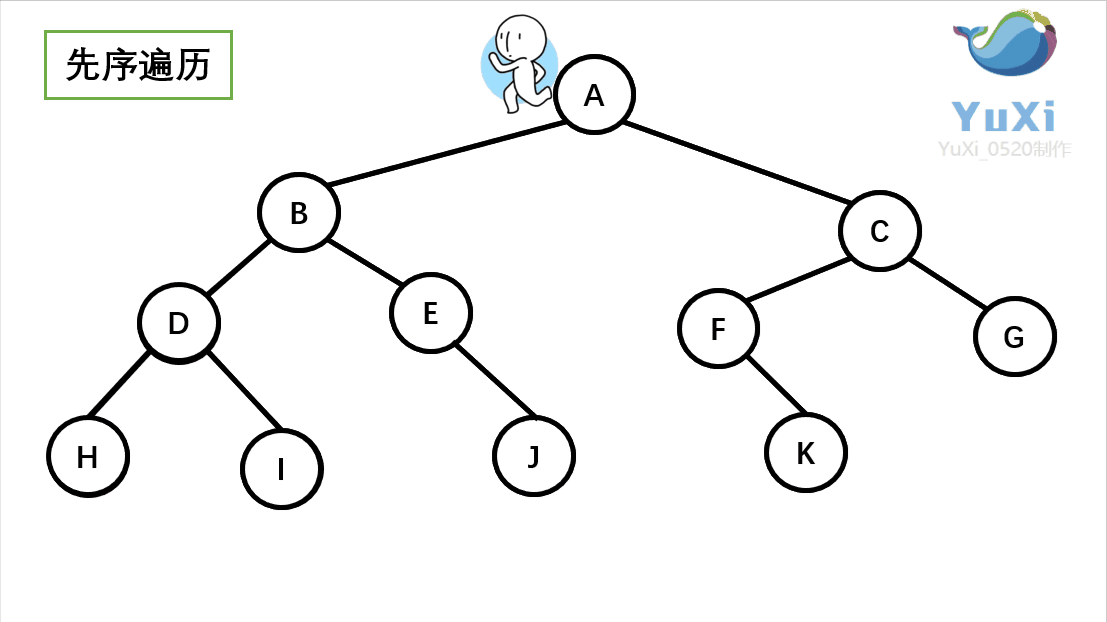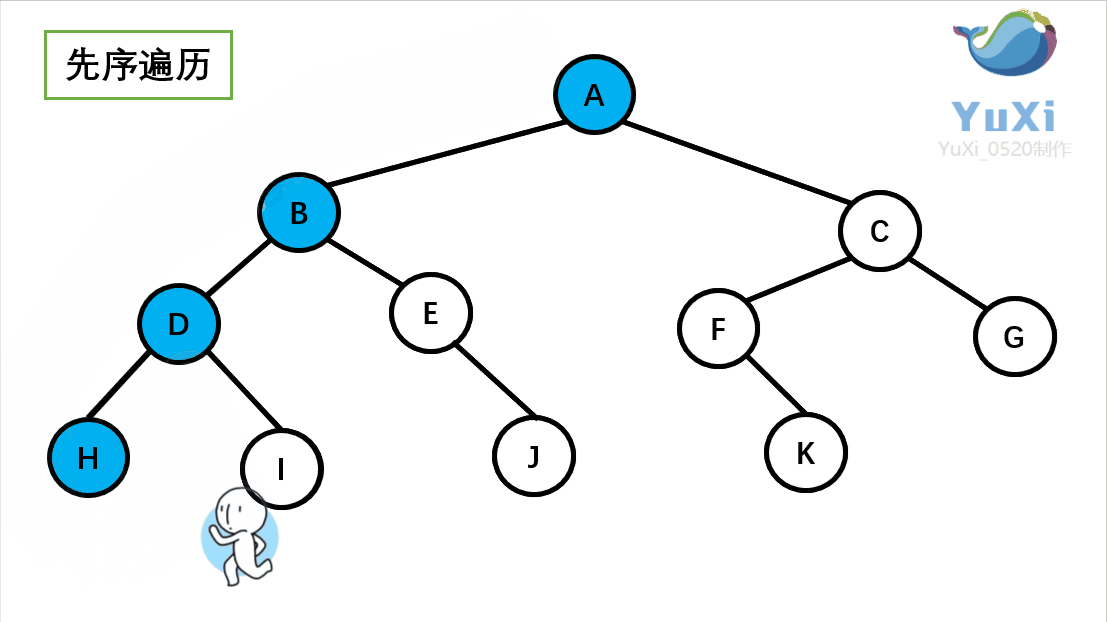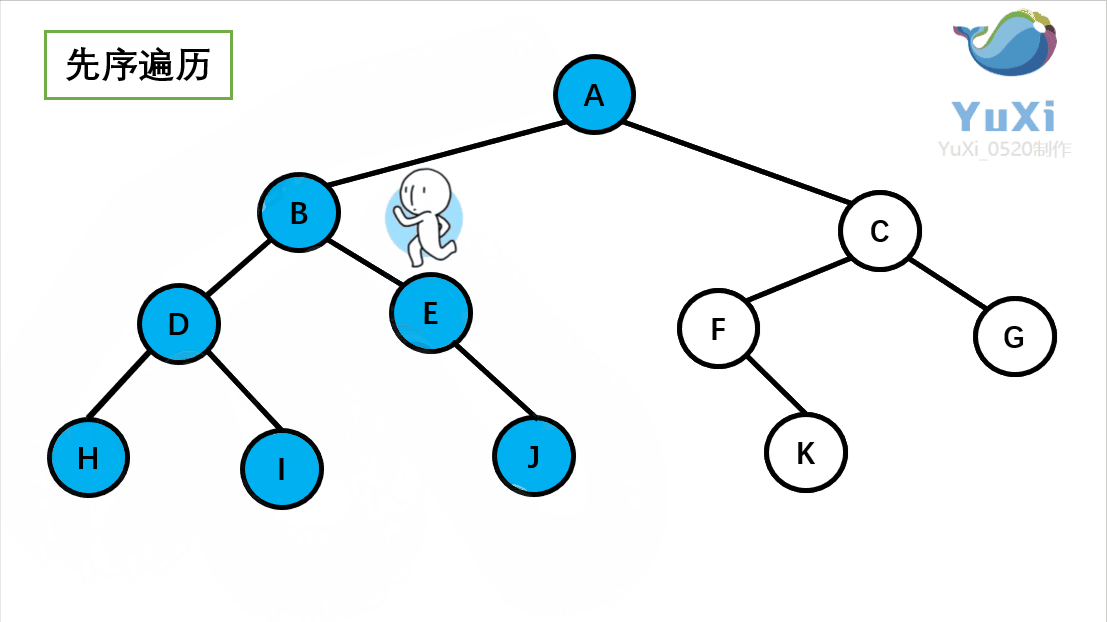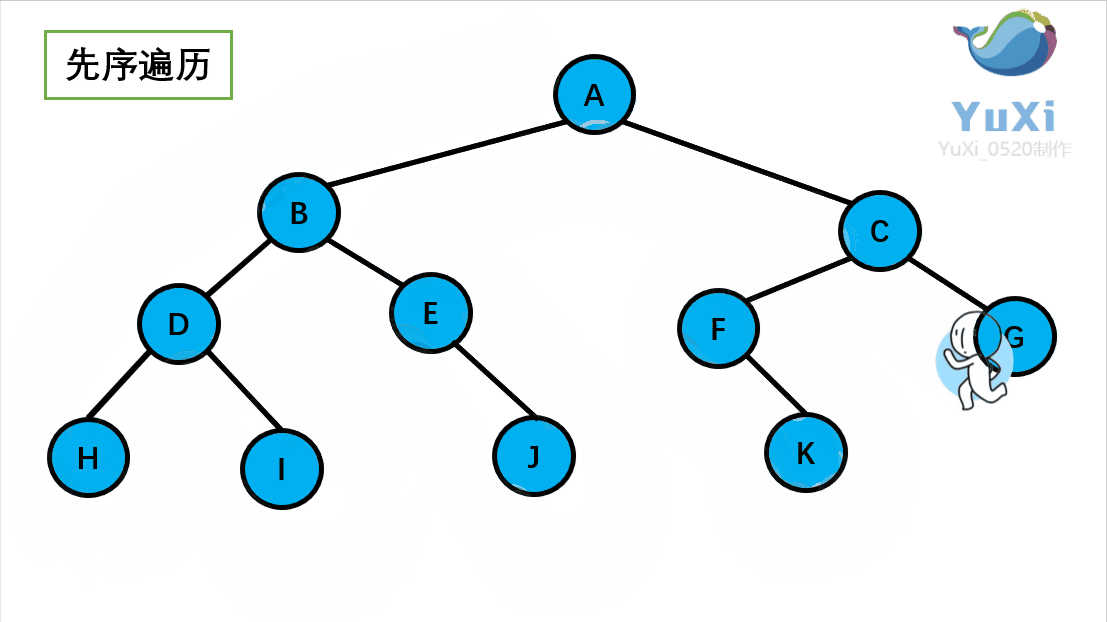
先序遍历可以想象为，一个小人从一棵二叉树根节点为起点，沿着二叉树外沿，逆时针走一圈回到根节点，路上遇到的元素顺序，就是先序遍历的结果

先序遍历结果为：A B D H I E J C F K G

动画演示：

记住小人沿着外围跑一圈（直到跑回根节点），多看几次动图便能理解

（2）中序遍历

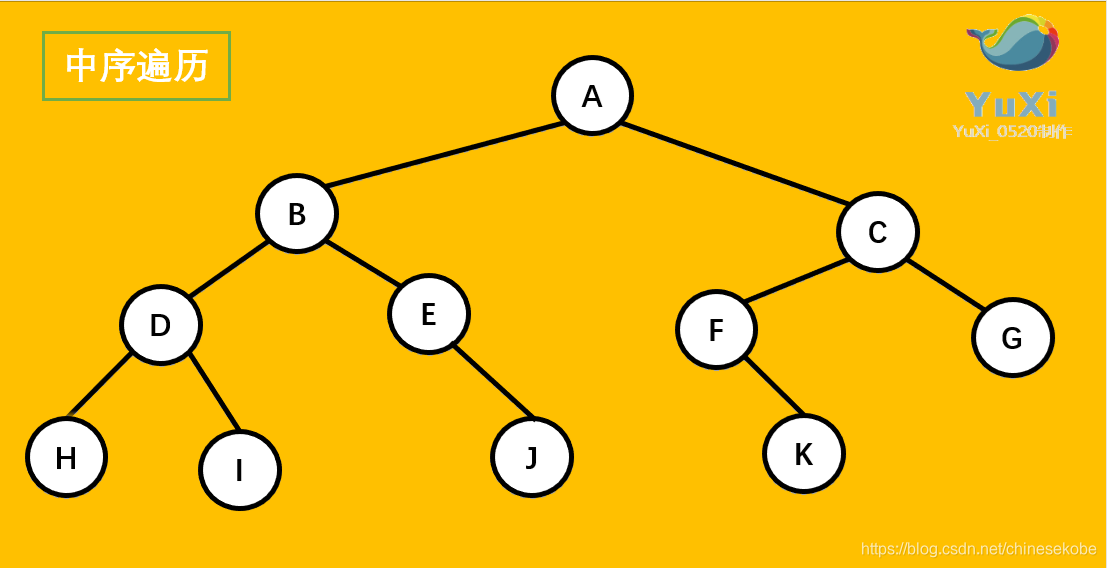
中序遍历可以看成，二叉树每个节点，垂直方向投影下来（可以理解为每个节点从最左边开始垂直掉到地上），然后从左往右数，得出的结果便是中序遍历的结果

中遍历结果为：H D I B E J A F K C G

动画展示：

记住，中序遍历就是从最左边开始，把每个节点垂直投影到同一直线上，然后从左往右读值就可以了，多看几遍动图就理解了

（3）后序遍历

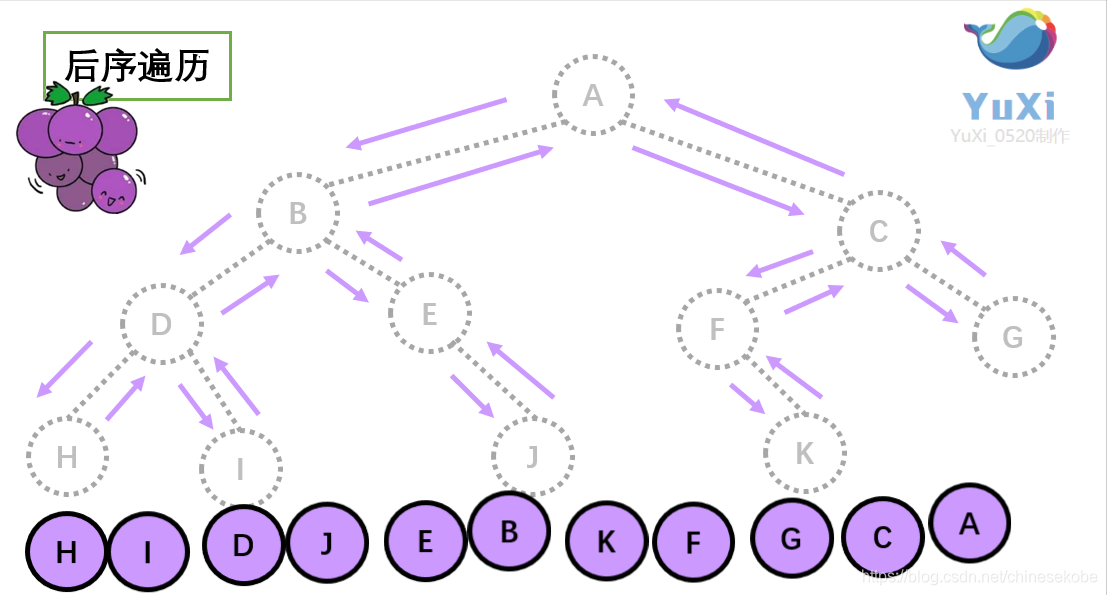
后序遍历就像是剪葡萄，我们要把一串葡萄剪成一颗一颗的。

还记得我上面提到先序遍历绕圈的路线么？（不记得翻上面理解）

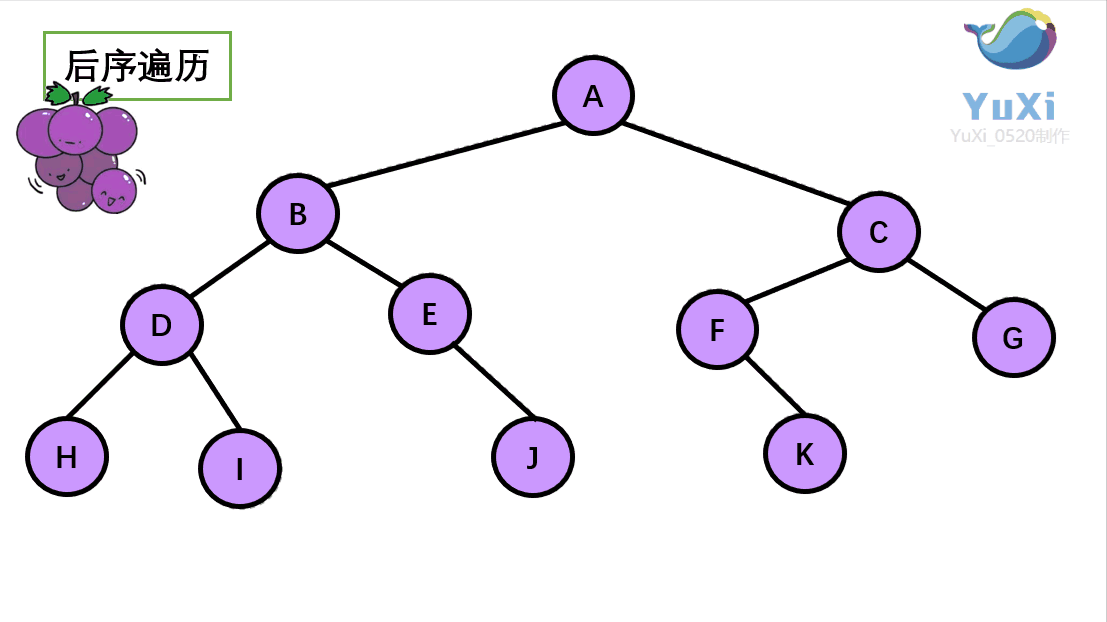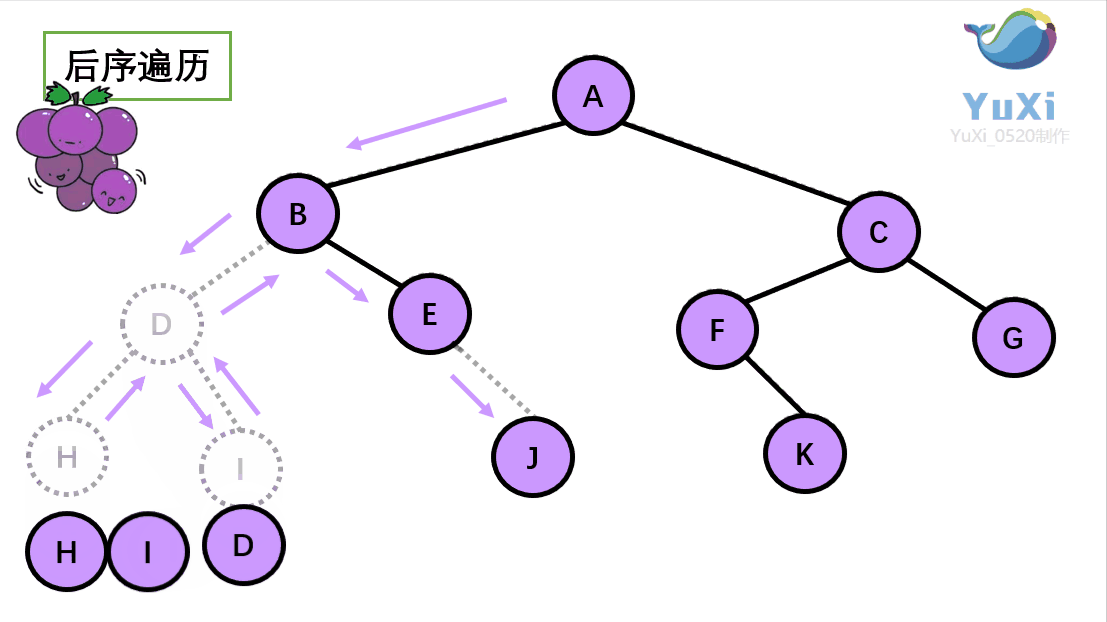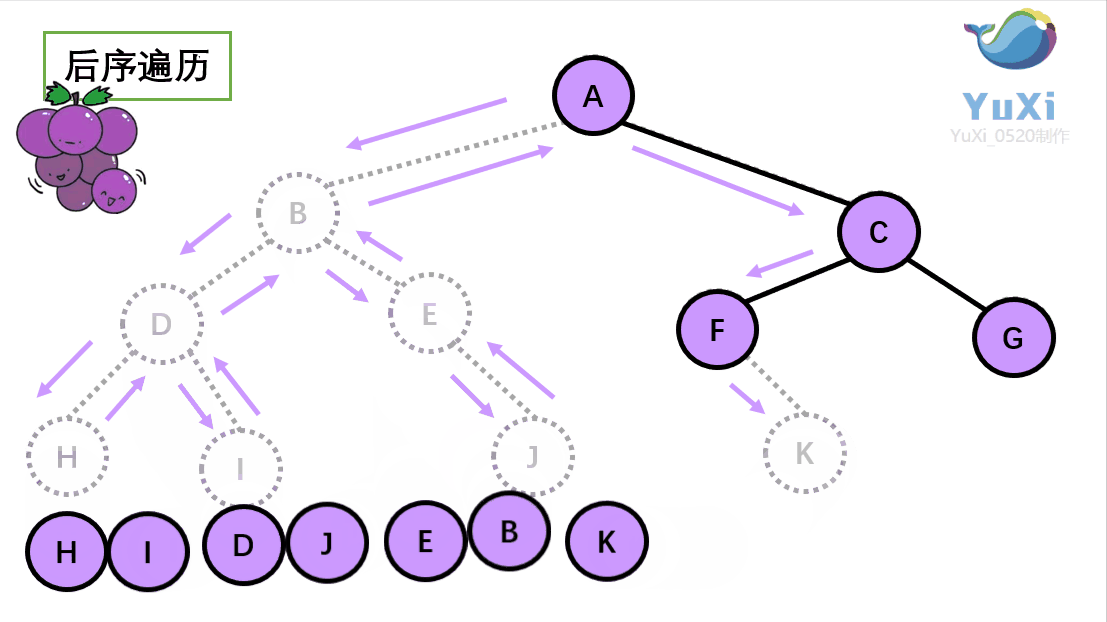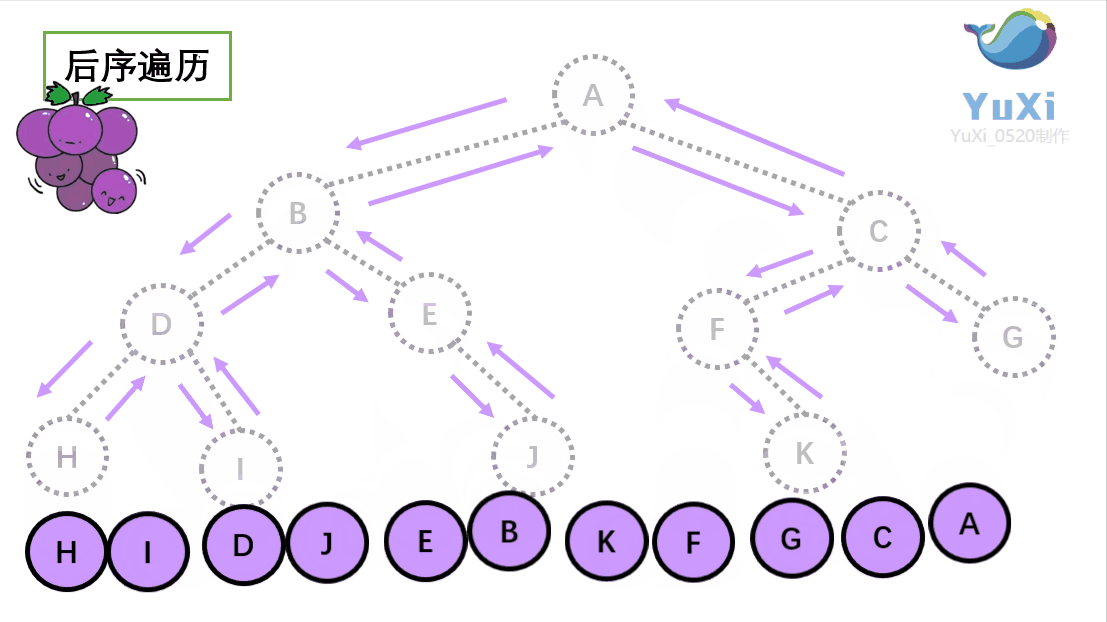
就是围着树的外围绕一圈，如果发现一剪刀就能剪下的葡萄（必须是一颗葡萄）（也就是葡萄要一个一个掉下来，不能一口气掉超过1个这样），就把它剪下来，组成的就是后序遍历了。

后序遍历中，根节点默认最后面

后序遍历结果：H I D J E B K F G C A

动画展示：

（4）层次遍历

层次遍历很好理解，就是从根节点开始，一层一层，从上到下，每层从左到右，依次写值就可以了

层次遍历结果：A B C D E F G H I J K

解释外圈跑的意思：

绕着外围跑一整圈的真正含义是：遍历所有结点时，都先往左孩子走，再往右孩子走。

（5）口诀

先序遍历： 先根 再左 再右

中序遍历： 先左 再根 再右

后序遍历： 先左 再右 再根

这里的根，指的是每个分叉子树（左右子树的根节点）根节点，并不只是最开始头顶的根节点，需要灵活思考理解，建议画图理解！！

二、代码展示：

#include<stdio.h>
#include<stdlib.h>

typedef struct Tree{
 
 int data;					//	存放数据域
 struct Tree *lchild;			//	遍历左子树指针
 struct Tree *rchild;			//	遍历右子树指针
 
}Tree,*BitTree;

BitTree CreateLink()
{
	int data;
	int temp;
	BitTree T;
	
	scanf("%d",&data);		//	输入数据
	temp=getchar();			//	吸收空格
	
	if(data == -1){			//	输入-1 代表此节点下子树不存数据，也就是不继续递归创建
		
		return NULL;

	}else{
		T = (BitTree)malloc(sizeof(Tree));			//		分配内存空间
		T->data = data;								//		把当前输入的数据存入当前节点指针的数据域中
		
		printf("请输入%d的左子树: ",data);		
		T->lchild = CreateLink();					//		开始递归创建左子树
		printf("请输入%d的右子树: ",data);			
		T->rchild = CreateLink();					//		开始到上一级节点的右边递归创建左右子树
		return T;							//		返回根节点
	}	
	
}
//	先序遍历
void ShowXianXu(BitTree T)			//		先序遍历二叉树
{
	if(T==NULL)						//	递归中遇到NULL，返回上一层节点
	{
		return;
	}
	printf("%d ",T->data);
	ShowXianXu(T->lchild);			//	递归遍历左子树
	ShowXianXu(T->rchild);			//	递归遍历右子树
}
//	中序遍历
void ShowZhongXu(BitTree T)			//		先序遍历二叉树
{
	if(T==NULL)						//	递归中遇到NULL，返回上一层节点
	{
		return;
	}
	
	ShowZhongXu(T->lchild);			//	递归遍历左子树
	printf("%d ",T->data);
	ShowZhongXu(T->rchild);			//	递归遍历右子树
	
}
//	后序遍历
void ShowHouXu(BitTree T)			//		后序遍历二叉树
{
	if(T==NULL)						//	递归中遇到NULL，返回上一层节点
	{
		return;
	}
	
	ShowHouXu(T->lchild);			//	递归遍历左子树
	ShowHouXu(T->rchild);			//	递归遍历右子树
	printf("%d ",T->data);
}


int main()
{
	BitTree S;
	printf("请输入第一个节点的数据:\n");
	S = CreateLink();			//		接受创建二叉树完成的根节点
	printf("先序遍历结果: \n");
	ShowXianXu(S);				//		先序遍历二叉树

	printf("\n中序遍历结果: \n");
	ShowZhongXu(S);				//		中序遍历二叉树
	
	printf("\n后序遍历结果: \n");
	ShowHouXu(S);				//		后序遍历二叉树
	
	return 0;	
}