「EZEC-4」可乐
洛谷:「EZEC-4」可乐
题目背景
很久以前,有一个 pigstd,非常迷恋美味的可乐。为了得到美味的可乐,他几乎用尽了所有的钱,他甚至对自己的 npy 也漠不关心其实是因为他没有npy,更不爱好看戏。除非买了新可乐,才会坐上马车出门炫耀一番。每一天,每个钟头他都要喝上一瓶新可乐。
pigstd 最近又买了许多箱新可乐——当然,这些可乐只有聪明的人才能喝到。
题目描述
pigstd 现在有 n n n 箱可乐,第 i i i 箱可乐上标着一个正整数 a i a_{i} ai。
若 pigstd 的聪明值为一个非负整数 x x x,对于第 i i i 箱可乐,如果 ( a i ⊕ x ) ≤ k (a_{i} \oplus x )\le k (ai⊕x)≤k,那么 pigstd 就能喝到这箱可乐。
现在 pigstd 告诉了你 k k k 与序列 a a a,你可以决定 pigstd 的聪明值 x x x,使得他能喝到的可乐的箱数最大。求出这个最大值。
输入格式
第一行两个由空格分隔开的整数 n , k n,k n,k。
接下来 n n n 行,每行一个整数 a i a_i ai,表示第 i i i 箱可乐上标的数。
输出格式
一行一个正整数,表示 pigstd 最多能喝到的可乐的箱数。
样例 #1
样例输入 #1
3 5
2
3
4
样例输出 #1
3
样例 #2
样例输入 #2
4 625
879
480
671
853
样例输出 #2
4
提示
提示
pigstd 的聪明值 x x x 可以为 0 0 0。
样例解释
样例 1 解释:容易构造当 x = 0 x = 0 x=0 时,可以喝到所有可乐。
样例 2 解释:容易构造 x = 913 x = 913 x=913,可以喝到所有可乐。
样例解释未必是唯一的方法。
数据范围
本题采用捆绑测试。
-
Subtask 1(29 points): 1 ≤ n , k , a i ≤ 1000 1 \le n,k,a_{i} \le 1000 1≤n,k,ai≤1000。
-
Subtask 2(1 points): a i ≤ k a_{i} \le k ai≤k。
-
Subtask 3(70 points):无特殊限制。
对于所有数据,保证 1 ≤ n , k , a i ≤ 1 0 6 1 \le n,k,a_{i} \le 10^6 1≤n,k,ai≤106。
⊕ \oplus ⊕ 代表异或,如果您不知道什么是异或,请单击这里。
方法1:位运算+差分
1、思路分析:
我们先分析一下这道题:
我们知道的是ai和k,那么我们可以根据这两者来推导可能的x。最后再所有可能的x中取一个最好的。
我们从高位开始枚举,情况可以根据k的二进制位划分为两大类:

继续枚举的原因很简单,就是因为k的前半部分和二者抑或后的结果的前半部分都是一样的,只能继续看后面的。
那么为什么有的就不用往后枚举了呢?
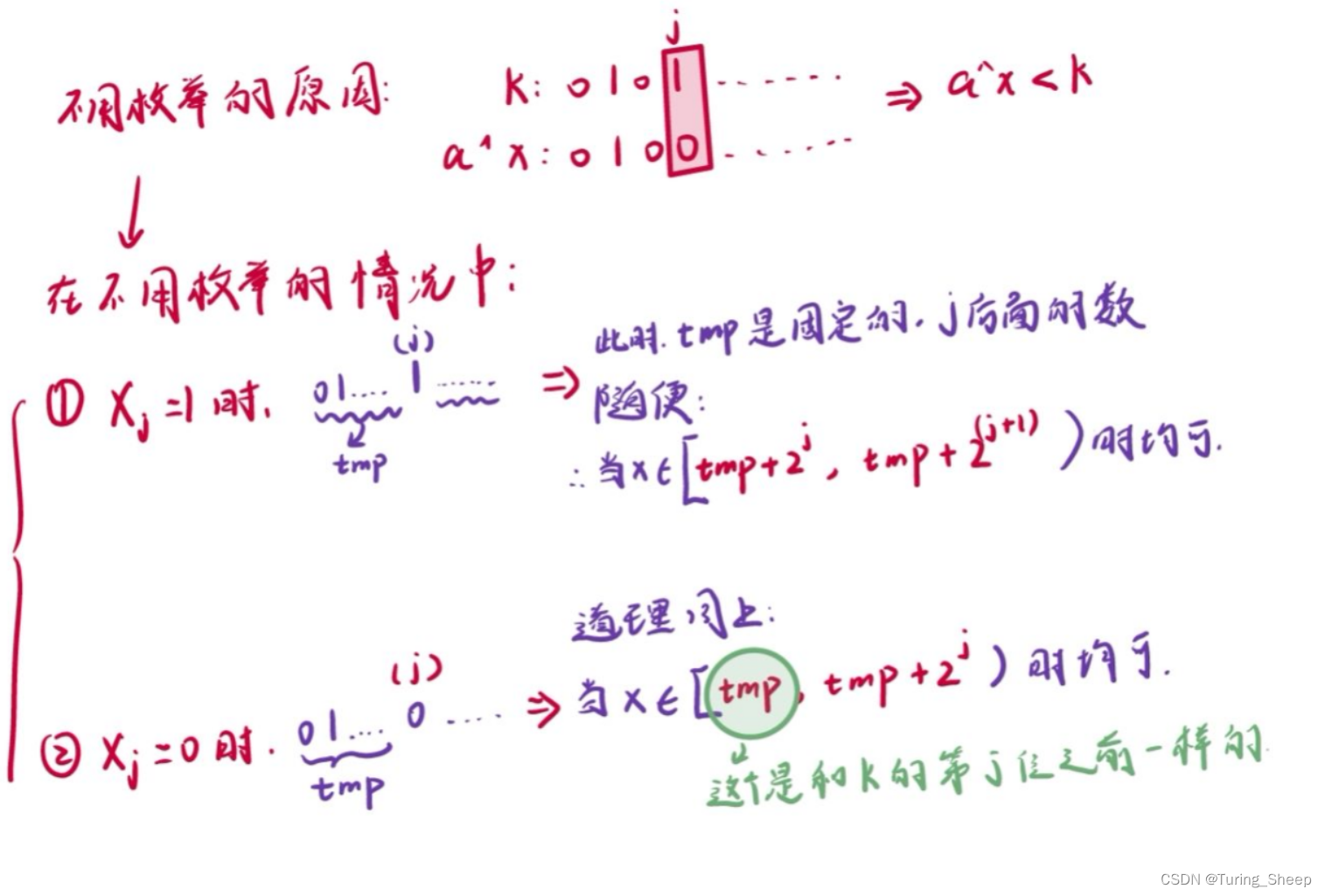
由此可知,如果把x的可能值画成一个数轴的话,此时再上面图片中的区间内的数可以整体+1,意思就是在这个区间内取X的时候,我们至少能够喝到1箱可乐。
那么我们看第二种情况:

因此,当k=0的时候,我们所有的可能情况只能是去更新我们的tmp。
那么对一个
a
i
a_i
ai而言,随着枚举的进行,x所形成的数轴变化如下:

那么上面三个区间合并在一起,就是能喝到当前可乐的所有x的取值。
那么对于每箱可乐,我们都找出这样一个区间,最后找到区间中重合最大的那部分,就是我们的x的最优解区间。
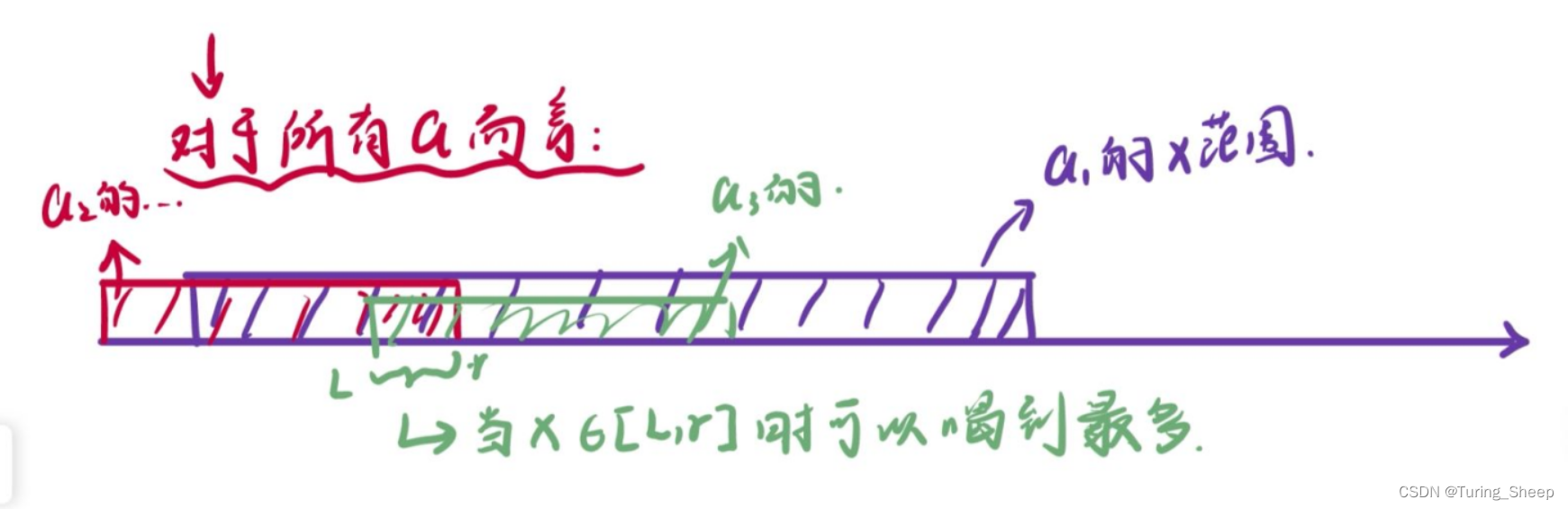
**而上述对于每个区间加上一个数的操作,我们可以使用差分。**这样的话,我们就可以从O(n)优化到O(1)。
2、代码实现:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e6+10,M=1<<20;
int a[N],x[M];
int n,k;
int main()
{
int n,k;
cin>>n>>k;
for(int i=0;i<n;i++)scanf("%d",a+i);
for(int i=0;i<n;i++)
{
int tmp=0;
for(int j=20;j>=0;j--)
{
if((k>>j)&1)
{
if((a[i]>>j)&1)
{
x[tmp+(1<<j)]++;
x[tmp+(1<<(j+1))]--;
}
else
{
x[tmp]++;
x[tmp+(1<<j)]--;
tmp+=1<<j;
}
}
else
{
if((a[i]>>j)&1)
tmp+=1<<j;
}
}
}
int res=x[0];
for(int i=1;i<M;i++)
{
x[i]+=x[i-1];
res=max(res,x[i]);
}
cout<<res<<endl;
return 0;
}
方法2:枚举+字典树
这道题给的数据范围是10的6次方,也就是说我们的x的最大值是 2 21 2^{21} 221左右,因此我们可以枚举这个 2 21 2^{21} 221个数字,这些数字就是可能的x的值,然后利用我们枚举的x去计算能喝到的可乐数目,在这些数目中取一个最大值。
但是这里有一个问题,我们的可乐箱数也有106的级别,我们判断一个x是否合理,就需要取枚举这106箱可乐。这样的话,我们的时间复杂度就到了1012次方。而一秒之内能够计算的次数大概在107到108左右。所以这种做法必定超时,而且超了10000多秒,这就相当恐怖了。
那么我们只能想优化了。
这些数必须得枚举,所以这106个x的可能取值,很难优化,那么只能优化判断这个x能够喝多少箱可乐这个过程了。
而我们优化的方式很简单,字典树。
因为我们用到了很多前缀的概念,所以我们可以把每个数字的二进制展开,然后建立成一个字典树。这样我们每次最多查询的次数等于边数,边数取决于我们一个数的二进制位数,由于题目数据的限制,我们最多遍历21条边。
因此,时间复杂度就是O(22121),大概是610的7次方。这个时间是可以算完的。
由于我们是枚举x,根据k去挑合法的a,所以核心思路就变成了根据x和k去推a。
所有的可能情况如下图所示:
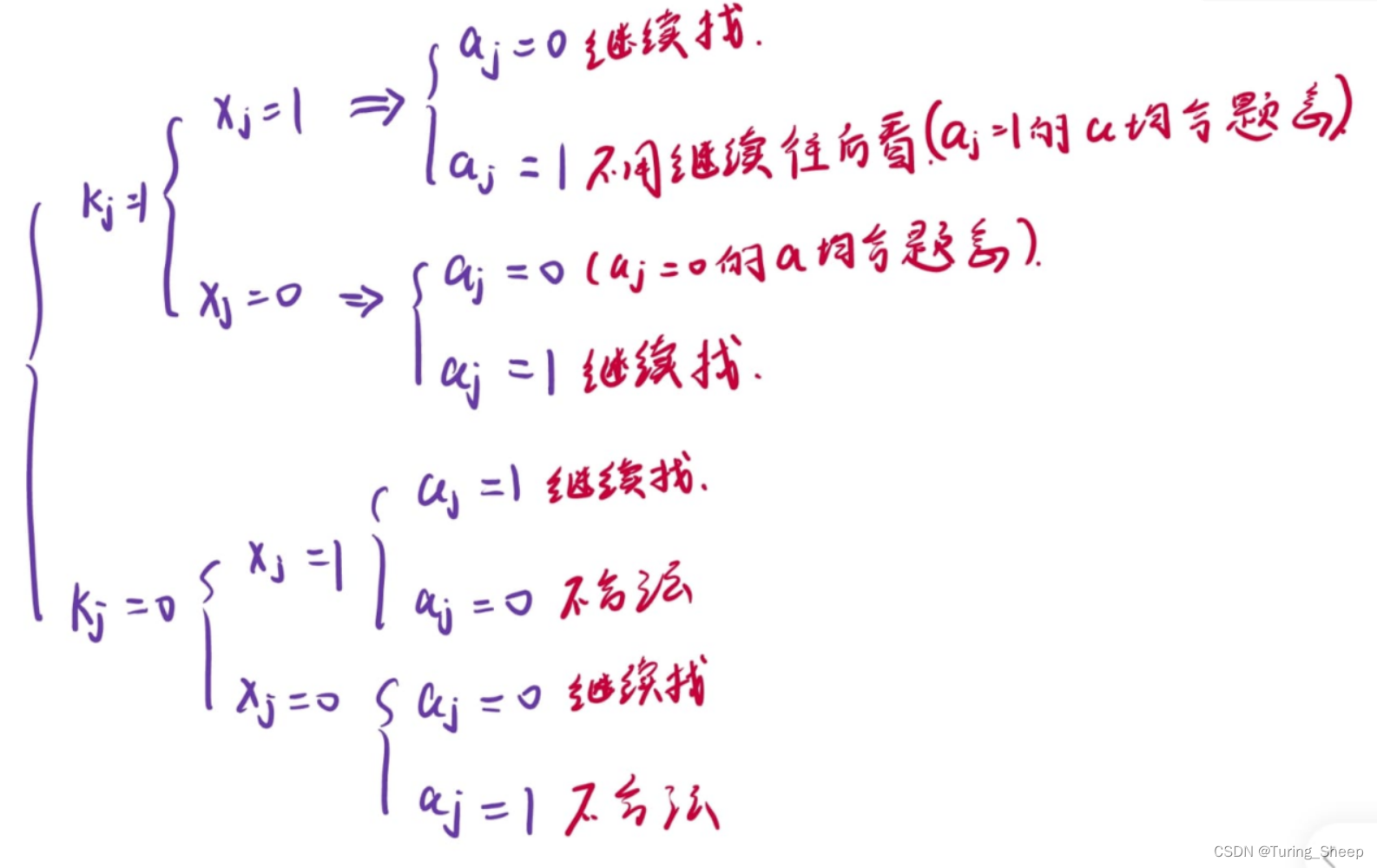
这里就不做过多的解释了。
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e6+10;
int son[N*21][2],cnt[N*21],idx;
int a[N],n,k;
void insert(int x)
{
int p=0;
for(int i=21;i>=0;i--)
{
int u=x>>i&1;
if(!son[p][u])son[p][u]=++idx;
p=son[p][u];
cnt[p]++;
}
}
int check(int x)
{
int p=0,sum=0;
int x_b,k_b;
for(int i=21;i>=0;i--)
{
x_b=(x>>i)&1,k_b=(k>>i)&1;
if(k_b)sum+=cnt[son[p][x_b]];
p=son[p][x_b^k_b];
if(!p)return sum;
}
sum+=cnt[p];
return sum;
}
int main()
{
cin>>n>>k;
for(int i=0;i<n;i++)
{
scanf("%d",a+i);
insert(a[i]);
}
int res=0;
for(int x=0;x<1<<21;x++)
{
res=max(res,check(x));
if(res==n)break;
}
cout<<res<<endl;
return 0;
}