目录
一、使用的方法
1.矩阵
2.矩阵的乘法原理
二、实例
1.源码
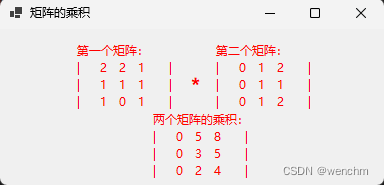
2.生成效果
一、使用的方法
矩阵相当于一个数组,主要用来存储一系列数,例如,m×n矩阵是排列在m行和n列中的一系列数,m×n矩阵可与一个n×p矩阵相乘,结果为一个m×p矩阵。这里需要注意的是,如果两个矩阵相乘,第一个矩阵的列数必须与第二个矩阵的行数相同。
1.矩阵
矩阵是指纵横排列的二维数据表格。
2.矩阵的乘法原理
矩阵乘法是一种高效的算法,它可以把一些一维递归优化到log(n),还可以求路径方案等。在执行两个矩阵的乘法运算时,需要将前面矩阵的第i行与后面矩阵的第j列对应的元素相乘,然后再相加,最后将得到的结果放到结果矩阵的第(i,j)这个位置上即可。
二、实例
1.源码
//矩阵乘法
namespace _108
{
public partial class Form1 : Form
{
static Label? label1;
static Label? label2;
static Label? label3;
static Label? label4;
public Form1()
{
InitializeComponent();
StartPosition = FormStartPosition.CenterScreen;
Load += Form1_Load;
}
private void Form1_Load(object? sender, EventArgs e)
{
//
// label1
//
label1 = new Label
{
AutoSize = true,
BackColor = SystemColors.Control,
ForeColor = Color.Red,
Location = new Point(74, 13),
Name = "label1",
Size = new Size(0, 17),
TabIndex = 0
};
//
// label2
//
label2 = new Label
{
AutoSize = true,
ForeColor = Color.Red,
Location = new Point(213, 13),
Name = "label2",
Size = new Size(0, 17),
TabIndex = 1
};
//
// label3
//
label3 = new Label
{
AutoSize = true,
Font = new Font("Microsoft YaHei UI", 14.25F, FontStyle.Bold, GraphicsUnit.Point, 134),
ForeColor = Color.Red,
Location = new Point(186, 43),
Name = "label3",
Size = new Size(21, 26),
TabIndex = 2,
Text = "*"
};
//
// label4
//
label4 = new Label
{
AutoSize = true,
ForeColor = Color.Red,
Location = new Point(150, 82),
Name = "label4",
Size = new Size(0, 17),
TabIndex = 3
};
//
// Form1
//
AutoScaleDimensions = new SizeF(7F, 17F);
AutoScaleMode = AutoScaleMode.Font;
ClientSize = new Size(384, 156);
Controls.Add(label4);
Controls.Add(label3);
Controls.Add(label2);
Controls.Add(label1);
Name = "Form1";
Text = "矩阵的乘积";
MatrixMulti();
}
static void MatrixMulti()
{
//定义3个float类型的二维数组,作为矩阵
float[,] Matrix1 = new float[3, 3];
float[,] Matrix2 = new float[3, 3];
float[,] MatrixResult = new float[3, 3];
//为第一个矩阵中的各个项赋值
Matrix1[0, 0] = 2;
Matrix1[0, 1] = 2;
Matrix1[0, 2] = 1;
Matrix1[1, 0] = 1;
Matrix1[1, 1] = 1;
Matrix1[1, 2] = 1;
Matrix1[2, 0] = 1;
Matrix1[2, 1] = 0;
Matrix1[2, 2] = 1;
//为第二个矩阵中的各个项赋值
Matrix2[0, 0] = 0;
Matrix2[0, 1] = 1;
Matrix2[0, 2] = 2;
Matrix2[1, 0] = 0;
Matrix2[1, 1] = 1;
Matrix2[1, 2] = 1;
Matrix2[2, 0] = 0;
Matrix2[2, 1] = 1;
Matrix2[2, 2] = 2;
label1!.Text += "第一个矩阵:\n";
//循环遍历第一个矩阵并逐行输出
for (int i = 0; i < 3; i++)
{
label1.Text += "| ";
for (int j = 0; j < 3; j++)
{
label1.Text += Matrix1[i, j] + " ";
}
label1.Text += " |\r\n";
}
label2!.Text = "第二个矩阵:\n";
//循环遍历第二个矩阵并逐行输出
for (int i = 0; i < 3; i++)
{
label2.Text += "| ";
for (int j = 0; j < 3; j++)
{
label2.Text += Matrix2[i, j] + " ";
}
label2.Text += " |\r\n";
}
MultiplyMatrix(Matrix1, Matrix2, MatrixResult);//调用自定义方法计算两个矩阵的乘积
label4!.Text = "两个矩阵的乘积:\n";
//循环遍历新得到的矩阵并逐行输出
for (int i = 0; i < 3; i++)
{
label4.Text += "| ";
for (int j = 0; j < 3; j++)
{
label4.Text += MatrixResult[i, j] + " ";
}
label4.Text += " |\r\n";
}
}
#region 矩阵乘法
/// <summary>
/// 在执行两个矩阵的乘法运算时,
/// 需要将前面矩阵的第i行与后面矩阵的第j列对应的元素相乘,
/// 然后再相加,最后将得到的结果放到结果矩阵的第(i,j)这个位置上即可。
/// </summary>
/// <param name="Matrix1"></param>
/// <param name="Matrix2"></param>
/// <param name="MatrixResult"></param>
public static void MultiplyMatrix(float[,] Matrix1, float[,] Matrix2, float[,] MatrixResult)
{
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
for (int k = 0; k < 3; k++)
{
MatrixResult[i, j] += Matrix1[i, k] * Matrix2[k, j];//计算矩阵的乘积
}
}
}
}
#endregion
}
}
2.生成效果