文章目录
- 前言
- 参考目录
- 学习笔记
- 1:基本算法
- 1.1:快速排序 demo 演示
- 1.2:快速排序切分代码实现
- 1.3:实现细节
- 1.4:案例分析
- 1.4.1:最佳案例
- 1.4.2:最坏案例
- 1.4.3:平均案例分析
- 1.5:特征总结
- 1.6:算法优化
- 2:Dijkstra 三向切分的快速排序
- 2.1:三向切分 demo 演示
- 2.2:三向切分代码实现
- 2.3:熵最优
- 3:排序算法小总结
前言
本章节主要内容是 快速排序。快速排序被誉为二十世纪十大算法之一,至今也十分常用。
本文的主要内容包括 快速排序 以及 三向切分快速排序,视频课程中还有关于快速选择(quick selection)以及计算机系统应用的一些说明,本文不详细展开,感兴趣的朋友建议移步视频自行学习总结。
参考目录
- B站 普林斯顿大学《Algorithms》视频课
(请自行搜索。主要以该视频课顺序来进行笔记整理,课程讲述的教授本人是该书原版作者之一 Robert Sedgewick。) - 微信读书《算法(第4版)》
(本文主要内容来自《2.3 快速排序》) - 官方网站
(有书本配套的内容以及代码)
学习笔记
注1:下面引用内容如无注明出处,均是书中摘录。
注2:所有 demo 演示均为视频 PPT demo 截图。
1:基本算法
快速排序的递归是在它完成工作之后,而归并排序是在它完成工作之前。
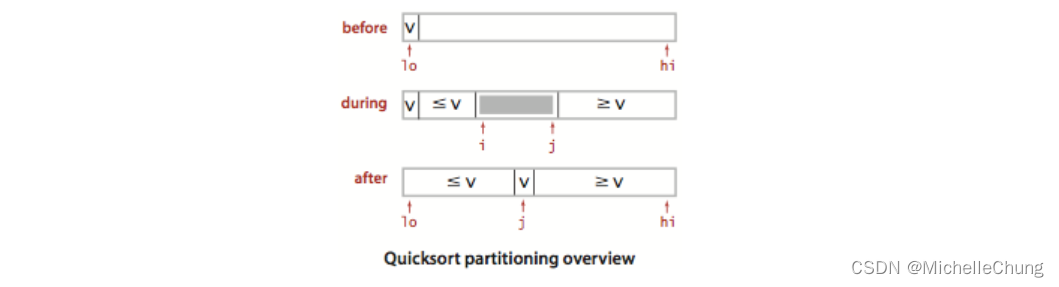
基本过程:
- 数组随机洗牌
- 用一些 j 分割数组:
- a[j] 在数组中
- j 左边都是比它小的数
- j 右边都是比它大的数
(对每一部分进行递归排序)
(截图自官网)
1.1:快速排序 demo 演示
阶段一:重复扫描直到指针 i 和 j 交叉。
- i 指针从左到右扫描,只要 a[i] < a[lo]
- j 指针从右到左扫描,只要 a[j] > a[lo]
- 交换 a[i] 和 a[j]
阶段二:当指针i和j交叉后
- 交换 a[lo] 和 a[j]
阶段二之后实际上就分区结束了。
(截图自官网)
切分轨迹:
(截图自官网)
1.2:快速排序切分代码实现
edu.princeton.cs.algs4.Quick#partition

edu.princeton.cs.algs4.Quick#sort

1.3:实现细节
(这里列出对应的章节)
- 2.3.1.1 原地切分
- 2.3.1.2 别越界
- 2.3.1.3 保持随机性
- 2.3.1.4 终止循环
- 2.3.1.5 处理切分元素值有重复的情况
- 2.3.1.6 终止递归
官网上也作了简单的说明:
(截图自官网)
1.4:案例分析
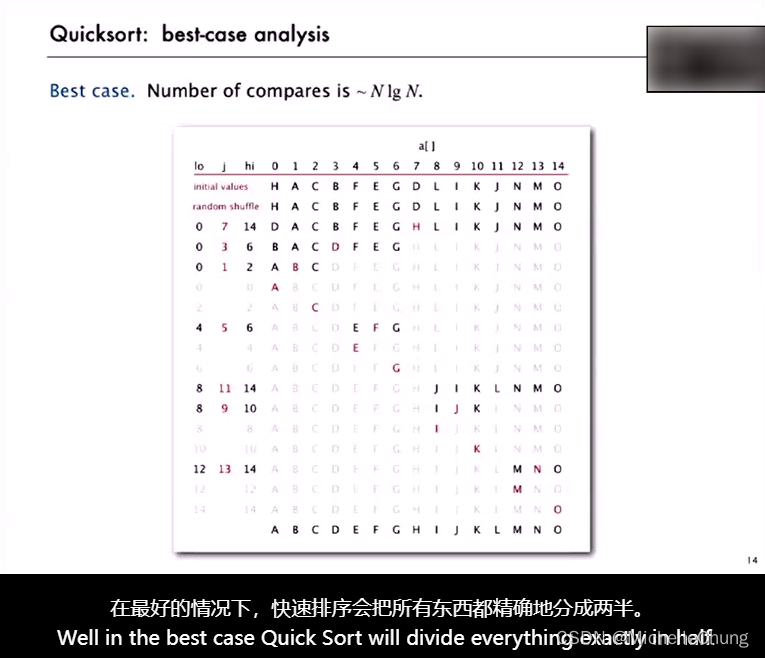
1.4.1:最佳案例
1.4.2:最坏案例
1.4.3:平均案例分析
这一环节,教授对于快速排序的分析作了数学模型的证明,对应了书本的命题 K。
命题K。将长度为N的无重复数组排序,快速排序平均需要~2NlnN次比较(以及1/6的交换)。
书本和教授视频里面都给出了相关的证明过程,不过说实话数学不好真的有点伤脑筋,我花了一点时间去搞懂证明过程。
先列举一下教授视频里面的证明过程:
特别是最后两步的近似过程,一开始一脸懵逼……
然后后面多亏了在线计算器,大致证明过程如下(iPad 写得比较丑,凑合看):



其中:

(https://mathdf.com/int/cn/)

(https://www.lddgo.net/math/logarithm-calculator)
1.5:特征总结
简单翻译一下:
最坏的情况:比较次数是平方级别
(不过你的电脑被闪电击中的可能性更大,可以参见命题L证明)
一般情况:比较数为 ~ 1.39NlgN
- 比较次数比归并排序多39%
- 但是实际上比归并排序更快,因为数据移动少
随机洗牌:
- 最坏情况下的概率保证
- 基本数学模型可以通过实验验证
需要注意。实际上很多教科书上的实现是平方级别的,假如数组:
- 进行排序或反向排序
- 有许多重复项(即使是随机的!)
快速排序是原地排序算法。
- 切分:恒定的额外空间
- 递归深度:对数额外空间(大概率)
(可以通过在较小的子数组上递归到较大的子数组来保证对数深度)
快速排序是不稳定的。
1.6:算法优化
- 2.3.3.1 切换到插入排序
- 2.3.3.2 三取样切分
- 2.3.3.3 熵最优的排序
2:Dijkstra 三向切分的快速排序
前面总结有提及到:如果有很多重复项的时候,快速排序会很慢。因而有了三向切分的优化方式。
(截图自官网)
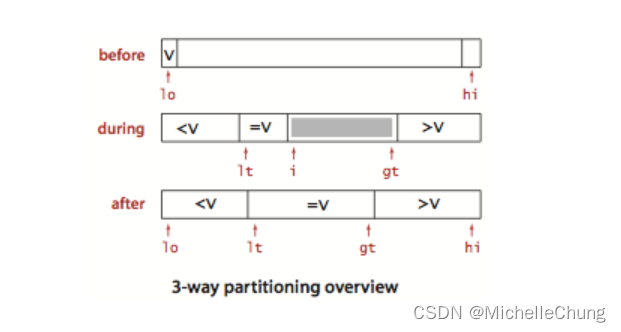
2.1:三向切分 demo 演示
初始数组:
情况一:a[i] < v
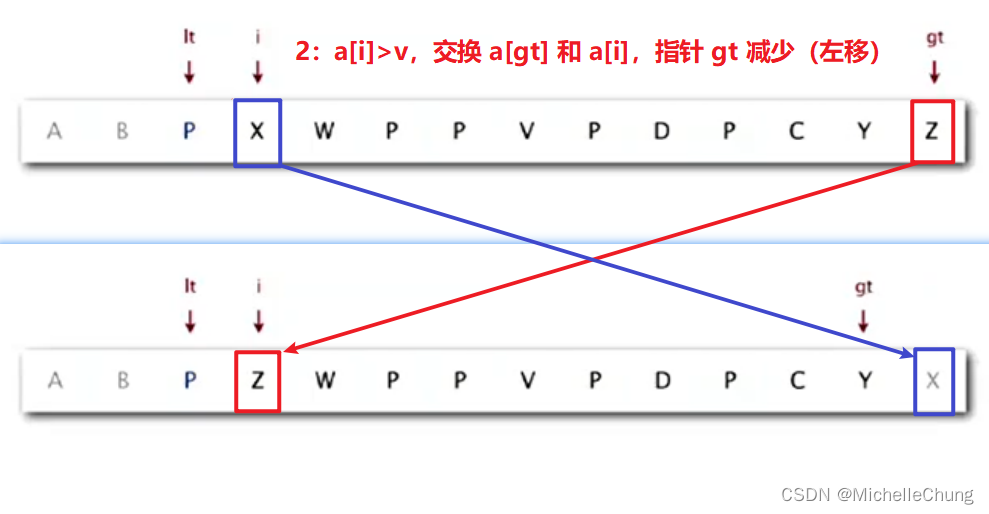
情况二:a[i] > v
情况三:a[i] = v
分割完成:
切分轨迹:
(截图自官网)
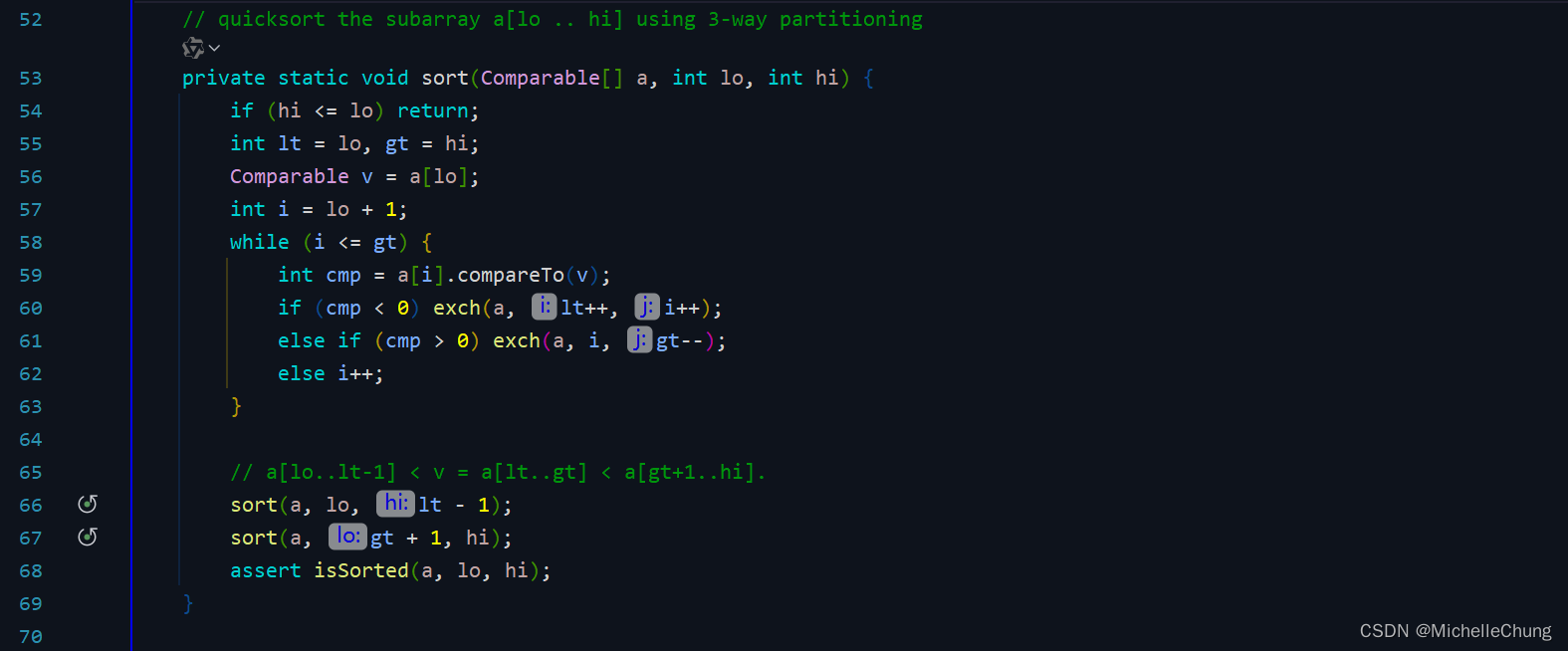
2.2:三向切分代码实现
教授:amazingly simple
edu.princeton.cs.algs4.Quick3way#sort
2.3:熵最优
(熵最优的证明超出了课程范围)
3:排序算法小总结
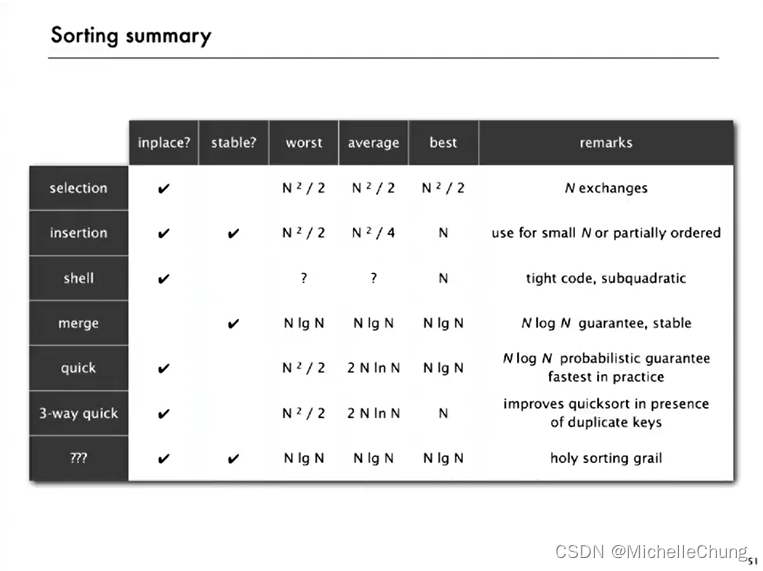
对于前面的六种算法作了简单总结:
做成表格简单翻译一下:
| 原地? | 稳定? | 最坏 | 平均 | 最好 | 备注 | |
|---|---|---|---|---|---|---|
| 选择排序 | √ | N2/2 | N2/2 | N2/2 | N次交换 | |
| 插入排序 | √ | √ | N2/2 | N2/4 | N | N较小或者是部分排序时使用 |
| 希尔排序 | √ | ? | ? | N | 编码紧凑,次平方时间复杂度 (次平方:指其运行时间的增长速度低于问题规模(通常是输入大小)的平方) | |
| 归并排序 | √ | NlgN | NlgN | NlgN | NlogN保证,稳定 | |
| 快速排序 | √ | N2/2 | 2NlnN | NlgN | NlogN概率保证,在实践中最快 | |
| 三向切分快速排序 | √ | N2/2 | 2NlnN | N | 改进存在重复键时的快排 | |
| ??? | √ | √ | NlgN | NlgN | NlgN | 排序的圣杯 (在计算机编程中,“Holy Sorting Grail”这个表达通常用来比喻一种理想化的排序算法。) |
(完)