《大学计算机—计算思维导论》（战德臣 哈尔滨工业大学）
《10.4 关系模型-关系运算》

一、引言

本章介绍数据库的基本数据模型：关系模型-关系运算。

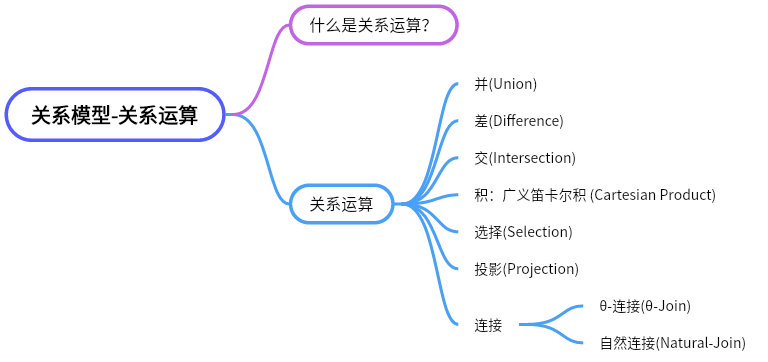
二、什么是关系运算

在数据库理论中，关系运算（Relational Operations）是一组用于操作和查询关系型数据库中数据的数学运算。这些运算主要针对的是二维表格形式的关系数据，通过这些运算可以合并和提取数据库表中的数据。

关系运算通常包括以下几个核心部分：

• 并：R ∪ S
• 差：R - S
• 交：R ∩ S
• 积：R × S
• 选择：σ（R）
• 投影：π（R）
• 连接：R ⋈ S

三、并运算

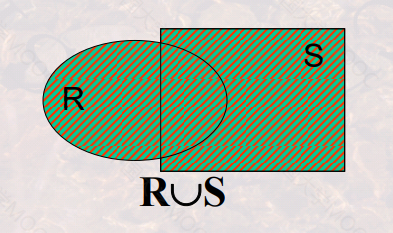
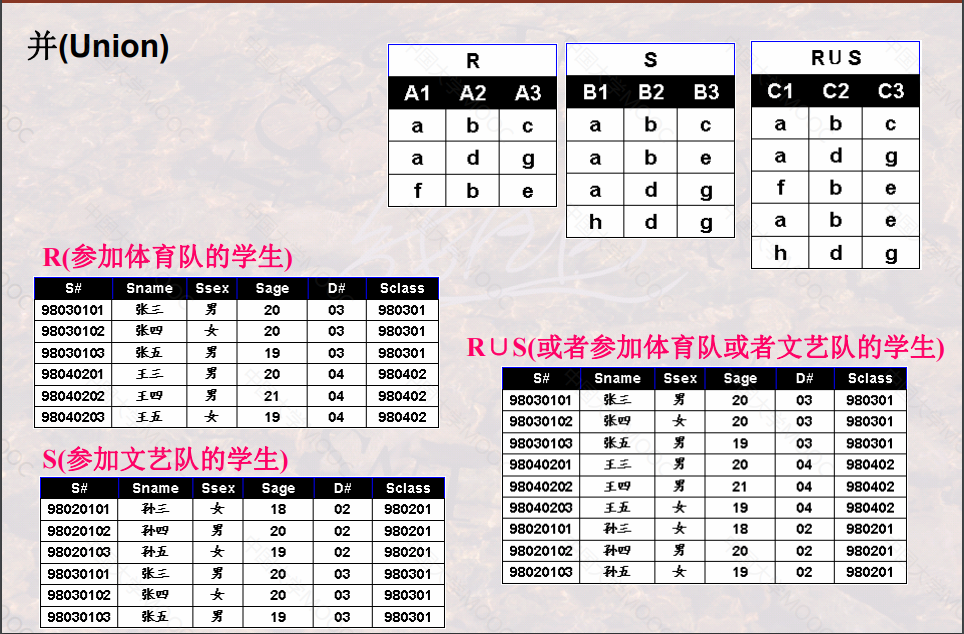
并(Union)

• 定义：设关系R和关系S是并相容的(即：属性数目相同，其对应的域也相同)，则关系R与关系S的并运算结果也是一个关系，记作： R∪S, 它由或者出现在关系R中，或者出现在S中的元组构成。
• 数学描述：R∪S = { t | t ∈ R v t ∈ S } ，其中 t 是元组。
• R ∪S 与 S ∪R 运算的结果是同一个关系

四、差运算

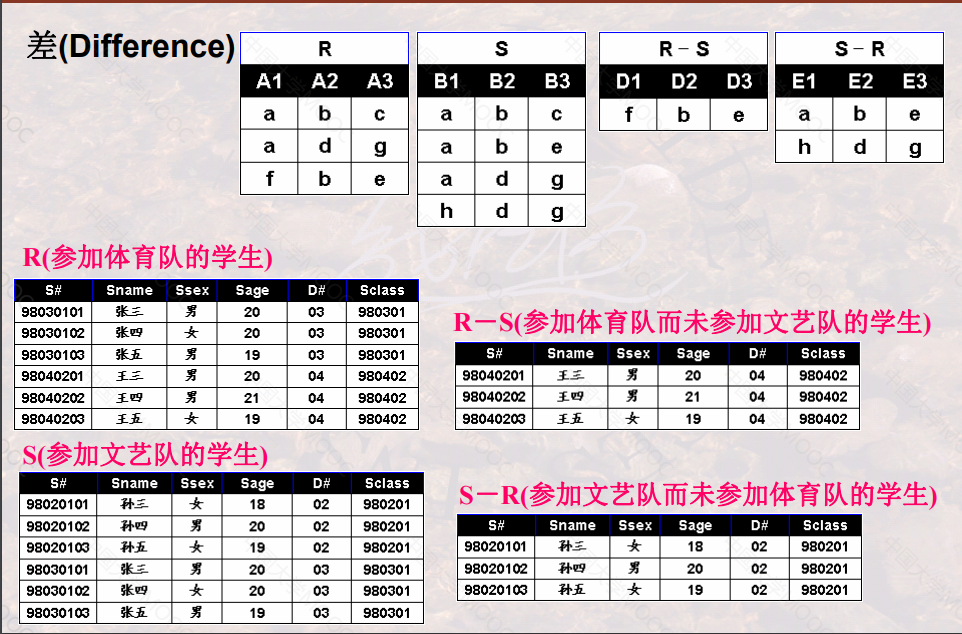
差(Difference)

• 定义：假设关系R和关系S是并相容的，则关系R 与关系S的差运算结果也是一个关系，记作：R - S, 它由出现在关系R中但不出现在关系S中的元组构成。
• 数学描述： R - S ={ t | t ∈ R ∧ t ∉ S } ，其中 t 是元组。
• 注意：R - S 与 S - R 是不同的。

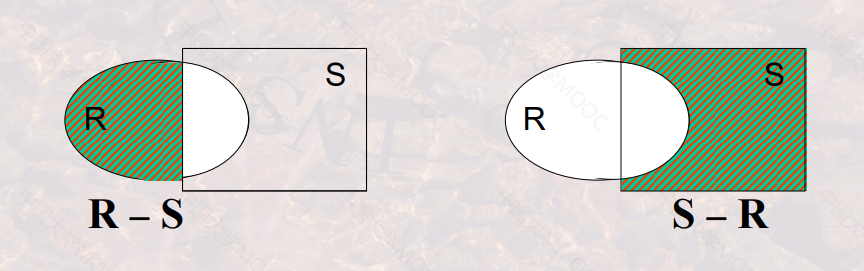
五、交运算

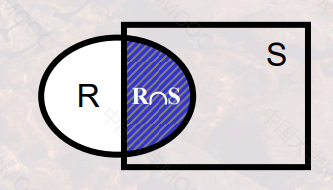
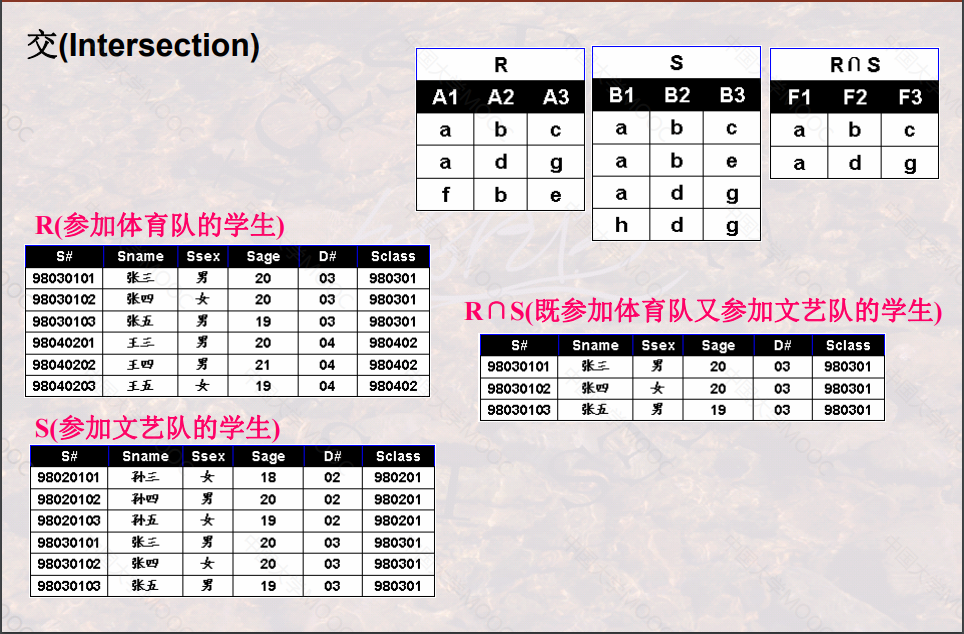
交(Intersection)

• 定义：假设关系R和关系S是并相容的，则关系R与关系S的交运算结果也是一个关系，记作：R∩S,它由同时出现在关系R和关系S中的元组构成。
• 数学描述： R∩S ={ t | t∈R∧t∈S } ，其中t是元组
• R∩S和S∩R 运算的结果是同一个关系
• 交运算可以通过差运算来实现：R∩S = R-(R-S) = S-(S-R)

六、笛卡尔积运算

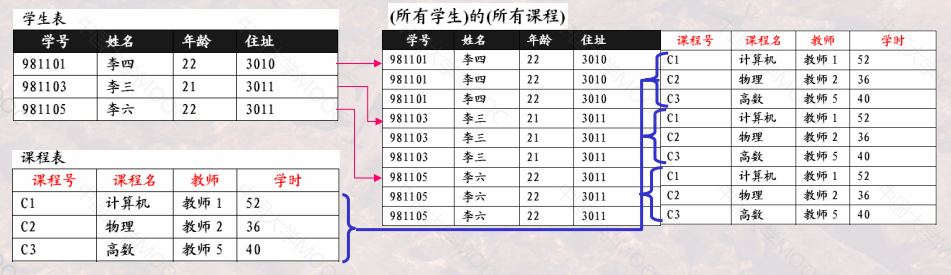
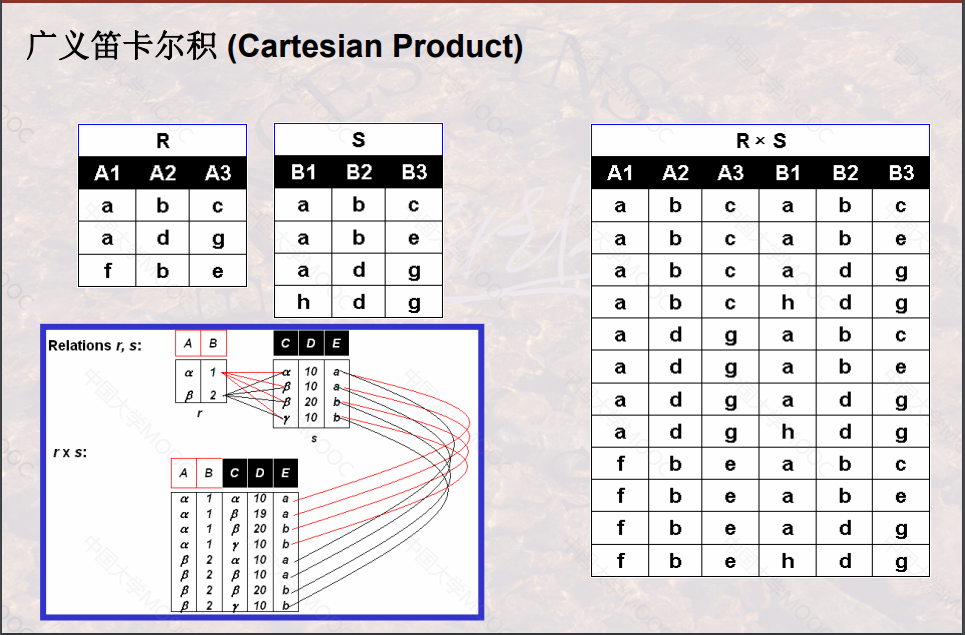
广义笛卡尔积 (Cartesian Product)

• 定义：关系R (<a1 , a2 , …, an >) 与关系S(<b1 , b2 , …, bm >) 的广义笛卡尔积(简称广义积) 运算结果也是一个关系，记作： R x S, 它由关系R中的元组与关系S的元组进行所有可能的拼接(或串接)构成。
• 数学描述： R x S ={ <a1 , a2 , …, an , b1 , b2 , …, bm > |<a1 , a2 , …, an > ∈R ∧<b1 , b2 , …, bm > ∈S }
• 笛卡尔积可将两个表串接起来作为一个表进行操作

七、选择运算

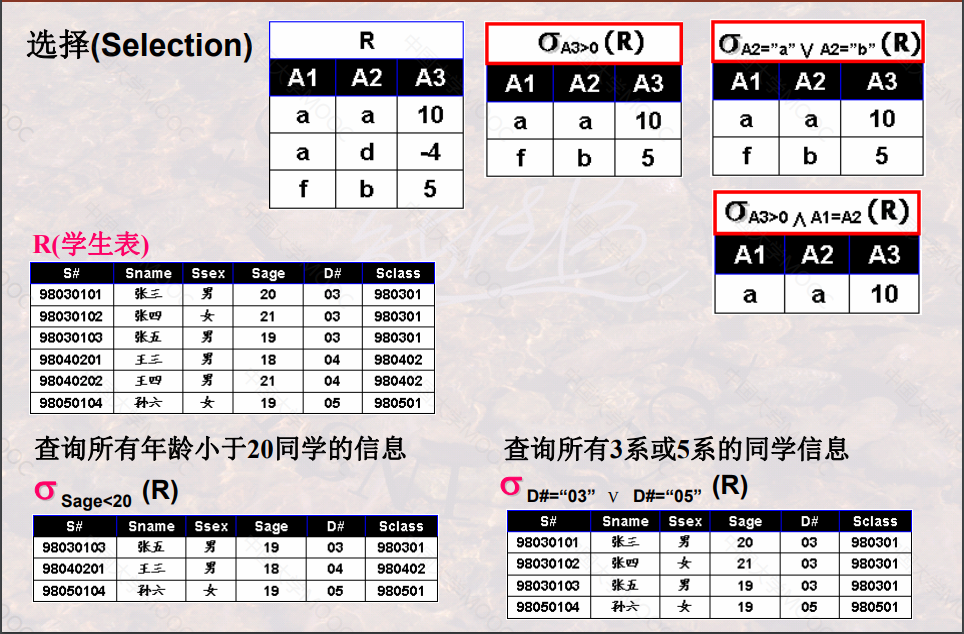
选择(Selection)

• 定义：给定一个关系R, 同时给定一个选择的条件condition(简记con),选择运算结果也是一个关系，记作 σ_con( R ), 它从关系R中选择出满足给定条件condition的元组构成
• 数学描述：σ_con( R )={t | t ( R )={t | t ∈ R ∧ con(t) =‘真’}

八、投影运算

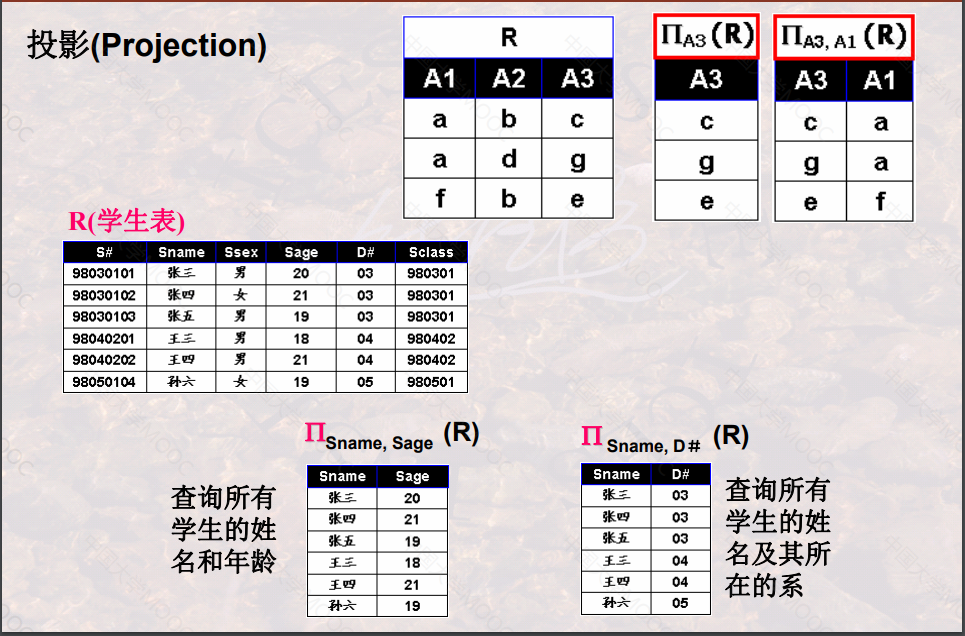
投影(Projection)

• 定义：给定一个关系R, 投影运算结果也是一个关系，记作 π_A ( R ), 它从关系R中选出属性包含在A中的列构成。
  

九、连接运算

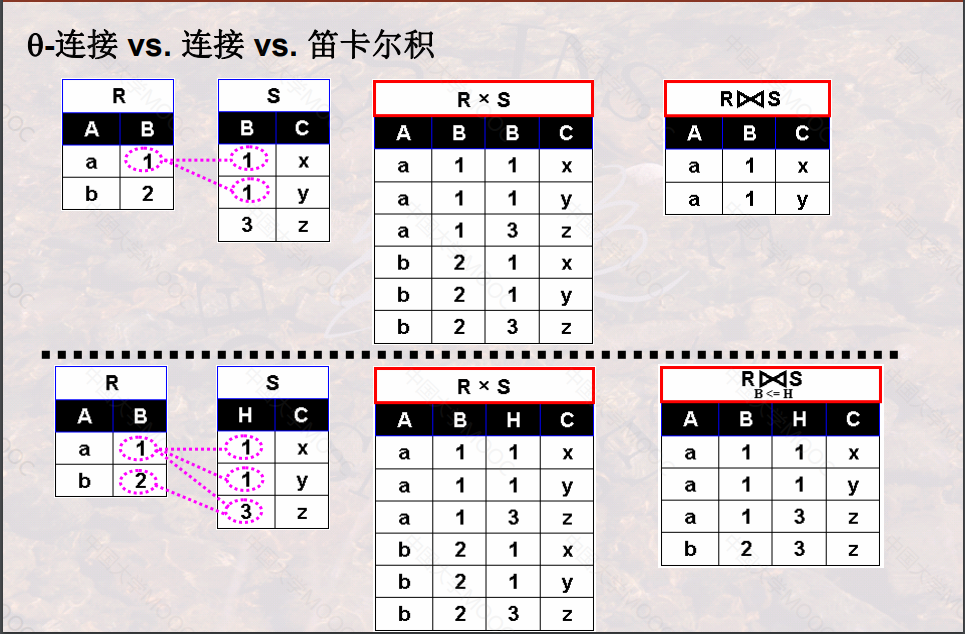
θ-连接(θ-Join)

自然连接(Natural-Join)

θ-连接 vs. 连接 vs. 笛卡尔积

十、小结

笛卡尔积和笛卡尔有什么关系？

笛卡尔积（Cartesian product）与笛卡尔（René Descartes）有直接的历史渊源关系。笛卡尔积这一数学概念正是以法国哲学家、数学家和物理学家勒内·笛卡尔（René Descartes）的名字命名的，他在17世纪的数学领域做出了重大贡献。

笛卡尔积是他提出的用来描述两个集合之间所有可能有序对组合的一种数学运算。具体来说，如果给定两个集合A和B，它们的笛卡尔积记作A×B，结果是一个新的集合，其中的元素是所有可能的有序对(a, b)，其中a是A中的元素，b是B中的元素。这个概念在现代数学的多个分支中都具有核心地位，特别是在集合论、代数、几何以及数据库理论等领域。