小游戏和GUI编程(5) | SVG图像格式简介

0. 问题

• Q1: SVG 是什么的缩写？
• Q2: SVG 是一种图像格式吗？
• Q3: SVG 相对于其他图像格式的优点和缺点是什么？
• Q4: 哪些工具可以查看 SVG 图像？
• Q5: SVG 图像格式的规范是怎样的？
• Q6: 通过写代码的方式，制作 SVG 图像?
• Q7: 高效制作 SVG 图像， 有哪些辅助工具可以使用？
• Q8: 怎样在 SFML 中加载 SVG 图像并显示?
• Q9: SVG 图像怎样转为 jpg/png 图像？

1. SVG 是什么的缩写？

A1: SVG 是 Scalable Vector Graphics 的缩写。

2. SVG 是一种图像格式吗？

.svg 文件是一个 XML 语言代码文件， 是一个图像。

矢量格式将图像存储为一组点和点之间的线。数学公式决定了这些点和线的位置和形状，并在放大或缩小图像时保持它们的空间关系。

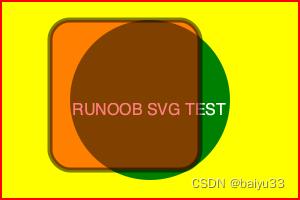
例如如下代码保存为 test.svg, 默认被浏览器打开图像并查看:

<svg version="1.1"
  baseProfile="full"
  width="300" height="200"
  xmlns="http://www.w3.org/2000/svg">

  <rect width="100%" height="100%" stroke="red" stroke-width="4" fill="yellow" />

  <circle cx="150" cy="100" r="80" fill="green" />

  <text x="150" y="115" font-size="16" text-anchor="middle" fill="white">RUNOOB SVG TEST</text>

</svg>

3. SVG 相对于其他图像格式的优点和缺点是什么？

SVG 相比于其他图像格式的优缺点：

优点：

• 编辑方便， 各种文本编辑器就可以编辑
• 文件较小， 毕竟是文本
• 清晰度不会随着放大缩小而影响

4. 哪些工具可以查看 SVG 图像？

哪些工具可以查看 SVG 图像？

• Edge 浏览器
• VSCode 默认不能查看， 安装 SVG 扩展后可以预览
• Beyond Compare: 会默认按照图像方式显示
• KolourPaint: 会默认按照图像方式显示
• PyCharm: 会同时显示 svg 文件的代码内容和图像内容
  

5. SVG 图像格式的规范是怎样的？

SVG 图像格式的规范:

• 以 <svg> 元素开始， 以 </svg> 结束。
• 支持预定义的形状元素: <rect>, <circle>, <ellipse>, <line>, <poliline>, <ploygon>, <path>
• 通过对每一种形状 tag 的属性进行设置， 来得到不同的效果, e.g.

  <rect x="50" y="20" rx="20" ry="20" width="150" height="150"
  style="fill:red;stroke:black;stroke-width:5;opacity:0.5"/>

• 支持滤镜
• 支持渐变

6. 通过写代码的方式，制作 SVG 图像?

通过写代码的方式，制作 SVG 图像

已经提到过了，就是 xml 代码， 只不过 tag 以及对应的属性， 是特殊的一小撮。

7. 高效制作 SVG 图像， 有哪些辅助工具可以使用？

高效制作 SVG 图像， 有哪些辅助工具可以使用？

https://www.jyshare.com/more/svgeditor/

这个在线工具， 是用鼠标的交互方式， 让人选择形状进行组合。 然后可以查看 svg 的源代码， 也可以转为 png 等图像格式。

8. 怎样在 SFML 中加载 SVG 图像并显示?

高效制作 SVG 图像， 有哪些辅助工具可以使用？

对于通过写代码方式生成 svg 图像， 主要在于编辑后的预览。 VSCode 里搜索 svg 扩展后排名第一个的那个扩展就可以了。

对于使用鼠标交互式生成 svg 图像， 使用 InkScape.

9. SVG 图像怎样转为 jpg/png 图像？

SVG 图像怎样转为 jpg/png 图像？

VSCode 插件
VSCode 里的 SVG 插件在预览时， 最右边一个图标是导出为 png 图像。

cairosvg 命令行工具

pip install cairosvg
cairosvg test.svg -o test.png

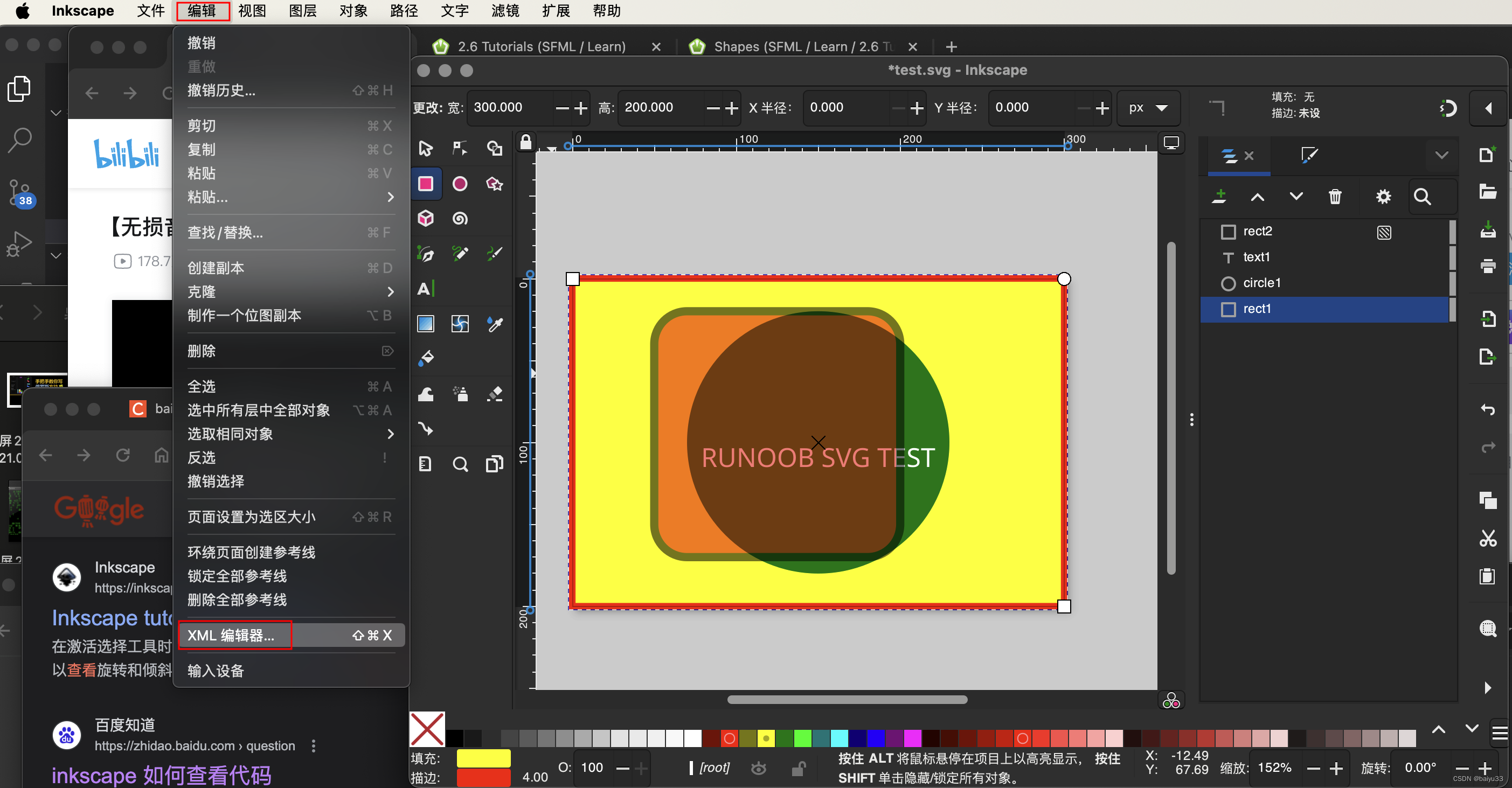
inkscape

inkscape 是世界上最先进的交互式编辑 svg 的软件， 支持各个操作系统。 也可以查看 xml 代码:

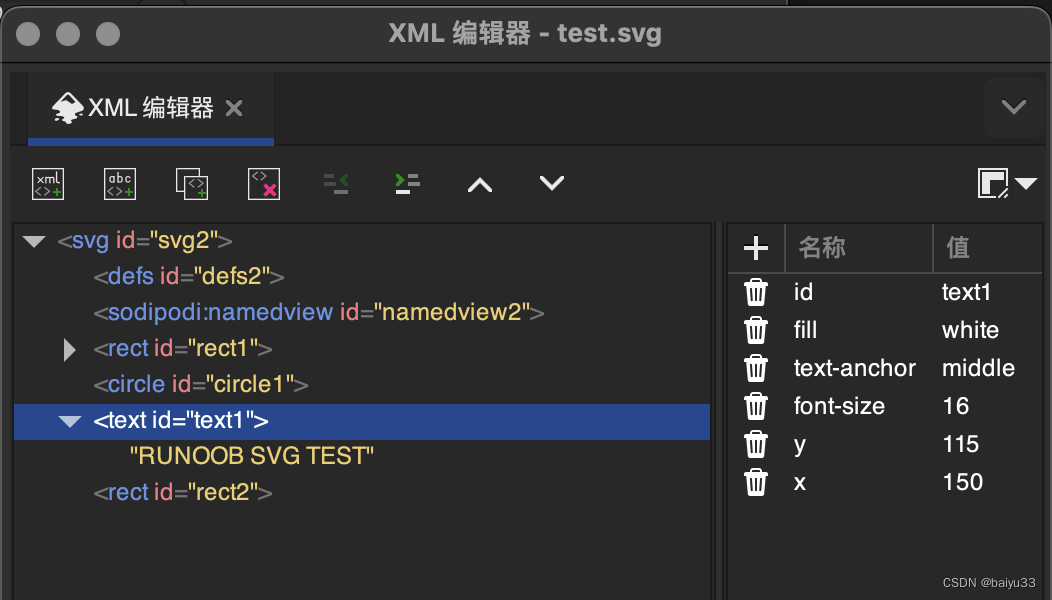
10. 总结

svg 格式的详细规范没找到， 乍一看简单的例子， 都是 xml 代码， 比较简单现查现用也来得及。

最为非nodejs程序员， 同行用 VSCode 的 svg 扩展， 就可以编写 svg 代码变看效果了。

如果希望鼠标点一点，组合各种形状， 首推 inkscape 软件, 其次是一些在线工具如: https://www.jyshare.com/more/svgeditor/

References

• https://www.runoob.com/svg/svg-intro.html
• https://superuser.com/questions/134679/command-line-application-for-converting-svg-to-png-on-mac-os-x
• https://developer.mozilla.org/zh-CN/docs/Web/SVG/Tutorial/Tools_for_SVG
• https://inkscape.org/zh-hans/doc/tutorials/basic/tutorial-basic.html