目录

1. 前言

2. 优化策略介绍

3. 新前与旧前

4. 新后与旧后

5. 新后与旧前

6. 新前与旧后

7. 回到源码

8. 总结

---

1. 前言

在上一篇文章中，我们介绍了当新的VNode与旧的oldVNode都是元素节点并且都包含子节点时，Vue对子节点是

先外层循环newChildren数组，再内层循环oldChildren数组，每循环外层newChildren数组里的一个子节点，就去内层oldChildren数组里找看有没有与之相同的子节点，最后根据不同的情况作出不同的操作。

在上一篇文章的结尾我们也说了，这种方法虽然能够解决问题，但是还存在可优化的地方。比如当包含的子节点数量很多时，这样循环算法的时间复杂度就会变的很大，不利于性能提升。当然，Vue也意识到了这点，并对此也进行了优化，那么本篇文章，就来学习一下关于子节点更新的优化问题Vue是如何做的。

2. 优化策略介绍

假如我们现有一份新的newChildren数组和旧的oldChildren数组，如下所示：

newChildren = ['新子节点1','新子节点2','新子节点3','新子节点4']
oldChildren = ['旧子节点1','旧子节点2','旧子节点3','旧子节点4']

如果按照优化之前的解决方案，那么我们接下来的操作应该是这样的：先循环newChildren数组，拿到第一个新子节点1，然后用第一个新子节点1去跟oldChildren数组里的旧子节点逐一对比，如果运气好一点，刚好oldChildren数组里的第一个旧子节点1与第一个新子节点1相同，那就皆大欢喜，直接处理，不用再往下循环了。那如果运气坏一点，直到循环到oldChildren数组里的第四个旧子节点4才与第一个新子节点1相同，那此时就会多循环了4次。我们不妨把情况再设想的极端一点，如果newChildren数组和oldChildren数组里前三个节点都没有变化，只是第四个节点发生了变化，那么我们就会循环16次，只有在第16次循环的时候才发现新节点4与旧节点4相同，进行更新，如下图所示： 

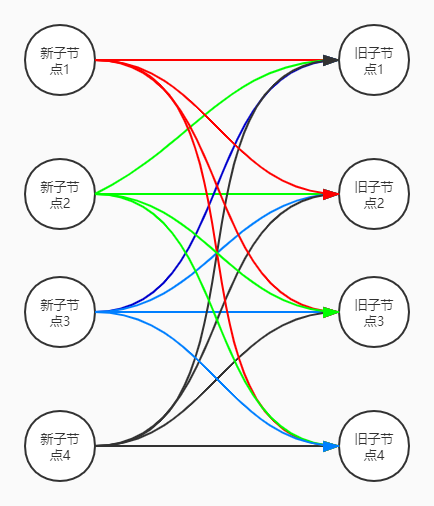
上面例子中只有四个子节点，好像还看不出来有什么缺陷，但是当子节点数量很多的时候，算法的时间复杂度就会非常高，很不利于性能提升。

那么我们该怎么优化呢？其实我们可以这样想，我们不要按顺序去循环newChildren和oldChildren这两个数组，可以先比较这两个数组里特殊位置的子节点，比如：

• 先把newChildren数组里的所有未处理子节点的第一个子节点和oldChildren数组里所有未处理子节点的第一个子节点做比对，如果相同，那就直接进入更新节点的操作；
• 如果不同，再把newChildren数组里所有未处理子节点的最后一个子节点和oldChildren数组里所有未处理子节点的最后一个子节点做比对，如果相同，那就直接进入更新节点的操作；
• 如果不同，再把newChildren数组里所有未处理子节点的最后一个子节点和oldChildren数组里所有未处理子节点的第一个子节点做比对，如果相同，那就直接进入更新节点的操作，更新完后再将oldChildren数组里的该节点移动到与newChildren数组里节点相同的位置；
• 如果不同，再把newChildren数组里所有未处理子节点的第一个子节点和oldChildren数组里所有未处理子节点的最后一个子节点做比对，如果相同，那就直接进入更新节点的操作，更新完后再将oldChildren数组里的该节点移动到与newChildren数组里节点相同的位置；
• 最后四种情况都试完如果还不同，那就按照之前循环的方式来查找节点。

其过程如下图所示： 

在上图中，我们把：

• newChildren数组里的所有未处理子节点的第一个子节点称为：新前；
• newChildren数组里的所有未处理子节点的最后一个子节点称为：新后；
• oldChildren数组里的所有未处理子节点的第一个子节点称为：旧前；
• oldChildren数组里的所有未处理子节点的最后一个子节点称为：旧后；

OK，有了以上概念以后，下面我们就来看看其具体是如何实施的。

3. 新前与旧前

把newChildren数组里的所有未处理子节点的第一个子节点和oldChildren数组里所有未处理子节点的第一个子节点做比对，如果相同，那好极了，直接进入之前文章中说的更新节点的操作并且由于新前与旧前两个节点的位置也相同，无需进行节点移动操作；如果不同，没关系，再尝试后面三种情况。 

4. 新后与旧后

把newChildren数组里所有未处理子节点的最后一个子节点和oldChildren数组里所有未处理子节点的最后一个子节点做比对，如果相同，那就直接进入更新节点的操作并且由于新后与旧后两个节点的位置也相同，无需进行节点移动操作；如果不同，继续往后尝试。 

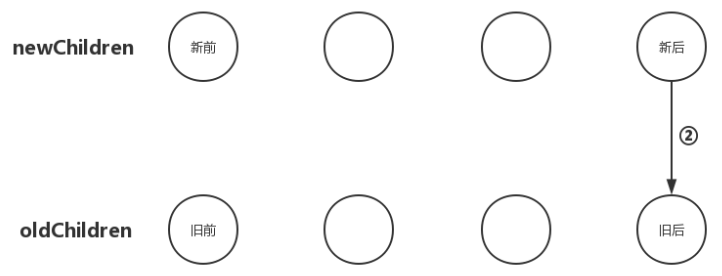
5. 新后与旧前

把newChildren数组里所有未处理子节点的最后一个子节点和oldChildren数组里所有未处理子节点的第一个子节点做比对，如果相同，那就直接进入更新节点的操作，更新完后再将oldChildren数组里的该节点移动到与newChildren数组里节点相同的位置； 

此时，出现了移动节点的操作，移动节点最关键的地方在于找准要移动的位置。我们一再强调，更新节点要以新VNode为基准，然后操作旧的oldVNode，使之最后旧的oldVNode与新的VNode相同。那么现在的情况是：newChildren数组里的最后一个子节点与oldChildren数组里的第一个子节点相同，那么我们就应该在oldChildren数组里把第一个子节点移动到最后一个子节点的位置，如下图：

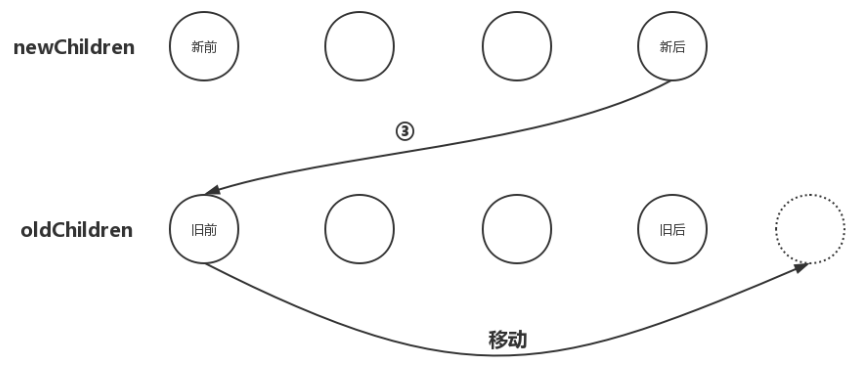
从图中不难看出，我们要把oldChildren数组里把第一个子节点移动到数组中所有未处理节点之后。

如果对比之后发现这两个节点仍不是同一个节点，那就继续尝试最后一种情况。

6. 新前与旧后

把newChildren数组里所有未处理子节点的第一个子节点和oldChildren数组里所有未处理子节点的最后一个子节点做比对，如果相同，那就直接进入更新节点的操作，更新完后再将oldChildren数组里的该节点移动到与newChildren数组里节点相同的位置；

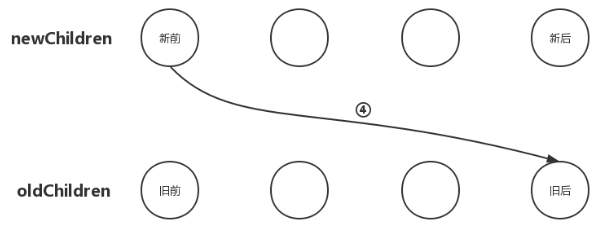
同样，这种情况的节点移动位置逻辑与“新后与旧前”的逻辑类似，那就是newChildren数组里的第一个子节点与oldChildren数组里的最后一个子节点相同，那么我们就应该在oldChildren数组里把最后一个子节点移动到第一个子节点的位置，如下图：

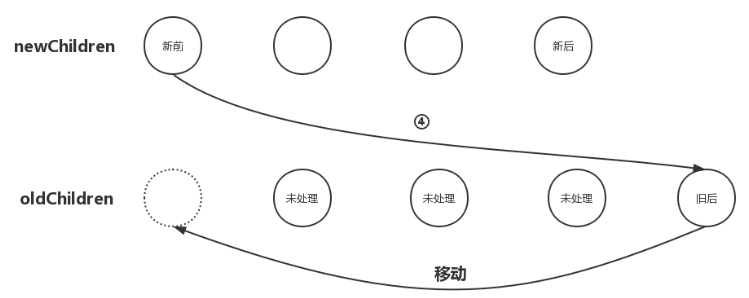
从图中不难看出，我们要把oldChildren数组里把最后一个子节点移动到数组中所有未处理节点之前。

OK，以上就是子节点对比更新优化策略种的4种情况，如果以上4种情况逐个试遍之后要是还没找到相同的节点，那就再通过之前的循环方式查找。

7. 回到源码

思路分析完，逻辑理清之后，我们再回到源码里看看，验证一下源码实现的逻辑是否跟我们分析的一样。源码如下：

// 循环更新子节点
  function updateChildren (parentElm, oldCh, newCh, insertedVnodeQueue, removeOnly) {
    let oldStartIdx = 0               // oldChildren开始索引
    let oldEndIdx = oldCh.length - 1   // oldChildren结束索引
    let oldStartVnode = oldCh[0]        // oldChildren中所有未处理节点中的第一个
    let oldEndVnode = oldCh[oldEndIdx]   // oldChildren中所有未处理节点中的最后一个

    let newStartIdx = 0               // newChildren开始索引
    let newEndIdx = newCh.length - 1   // newChildren结束索引
    let newStartVnode = newCh[0]        // newChildren中所有未处理节点中的第一个
    let newEndVnode = newCh[newEndIdx]  // newChildren中所有未处理节点中的最后一个

    let oldKeyToIdx, idxInOld, vnodeToMove, refElm

    // removeOnly is a special flag used only by <transition-group>
    // to ensure removed elements stay in correct relative positions
    // during leaving transitions
    const canMove = !removeOnly

    if (process.env.NODE_ENV !== 'production') {
      checkDuplicateKeys(newCh)
    }

    // 以"新前"、"新后"、"旧前"、"旧后"的方式开始比对节点
    while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
      if (isUndef(oldStartVnode)) {
        oldStartVnode = oldCh[++oldStartIdx] // 如果oldStartVnode不存在，则直接跳过，比对下一个
      } else if (isUndef(oldEndVnode)) {
        oldEndVnode = oldCh[--oldEndIdx]
      } else if (sameVnode(oldStartVnode, newStartVnode)) {
        // 如果新前与旧前节点相同，就把两个节点进行patch更新
        patchVnode(oldStartVnode, newStartVnode, insertedVnodeQueue)
        oldStartVnode = oldCh[++oldStartIdx]
        newStartVnode = newCh[++newStartIdx]
      } else if (sameVnode(oldEndVnode, newEndVnode)) {
        // 如果新后与旧后节点相同，就把两个节点进行patch更新
        patchVnode(oldEndVnode, newEndVnode, insertedVnodeQueue)
        oldEndVnode = oldCh[--oldEndIdx]
        newEndVnode = newCh[--newEndIdx]
      } else if (sameVnode(oldStartVnode, newEndVnode)) { // Vnode moved right
        // 如果新后与旧前节点相同，先把两个节点进行patch更新，然后把旧前节点移动到oldChilren中所有未处理节点之后
        patchVnode(oldStartVnode, newEndVnode, insertedVnodeQueue)
        canMove && nodeOps.insertBefore(parentElm, oldStartVnode.elm, nodeOps.nextSibling(oldEndVnode.elm))
        oldStartVnode = oldCh[++oldStartIdx]
        newEndVnode = newCh[--newEndIdx]
      } else if (sameVnode(oldEndVnode, newStartVnode)) { // Vnode moved left
        // 如果新前与旧后节点相同，先把两个节点进行patch更新，然后把旧后节点移动到oldChilren中所有未处理节点之前
        patchVnode(oldEndVnode, newStartVnode, insertedVnodeQueue)
        canMove && nodeOps.insertBefore(parentElm, oldEndVnode.elm, oldStartVnode.elm)
        oldEndVnode = oldCh[--oldEndIdx]
        newStartVnode = newCh[++newStartIdx]
      } else {
        // 如果不属于以上四种情况，就进行常规的循环比对patch
        if (isUndef(oldKeyToIdx)) oldKeyToIdx = createKeyToOldIdx(oldCh, oldStartIdx, oldEndIdx)
        idxInOld = isDef(newStartVnode.key)
          ? oldKeyToIdx[newStartVnode.key]
          : findIdxInOld(newStartVnode, oldCh, oldStartIdx, oldEndIdx)
        // 如果在oldChildren里找不到当前循环的newChildren里的子节点
        if (isUndef(idxInOld)) { // New element
          // 新增节点并插入到合适位置
          createElm(newStartVnode, insertedVnodeQueue, parentElm, oldStartVnode.elm, false, newCh, newStartIdx)
        } else {
          // 如果在oldChildren里找到了当前循环的newChildren里的子节点
          vnodeToMove = oldCh[idxInOld]
          // 如果两个节点相同
          if (sameVnode(vnodeToMove, newStartVnode)) {
            // 调用patchVnode更新节点
            patchVnode(vnodeToMove, newStartVnode, insertedVnodeQueue)
            oldCh[idxInOld] = undefined
            // canmove表示是否需要移动节点，如果为true表示需要移动，则移动节点，如果为false则不用移动
            canMove && nodeOps.insertBefore(parentElm, vnodeToMove.elm, oldStartVnode.elm)
          } else {
            // same key but different element. treat as new element
            createElm(newStartVnode, insertedVnodeQueue, parentElm, oldStartVnode.elm, false, newCh, newStartIdx)
          }
        }
        newStartVnode = newCh[++newStartIdx]
      }
    }
    if (oldStartIdx > oldEndIdx) {
      /**
       * 如果oldChildren比newChildren先循环完毕，
       * 那么newChildren里面剩余的节点都是需要新增的节点，
       * 把[newStartIdx, newEndIdx]之间的所有节点都插入到DOM中
       */
      refElm = isUndef(newCh[newEndIdx + 1]) ? null : newCh[newEndIdx + 1].elm
      addVnodes(parentElm, refElm, newCh, newStartIdx, newEndIdx, insertedVnodeQueue)
    } else if (newStartIdx > newEndIdx) {
      /**
       * 如果newChildren比oldChildren先循环完毕，
       * 那么oldChildren里面剩余的节点都是需要删除的节点，
       * 把[oldStartIdx, oldEndIdx]之间的所有节点都删除
       */
      removeVnodes(parentElm, oldCh, oldStartIdx, oldEndIdx)
    }
  }

读源码之前，我们先有这样一个概念：那就是在我们前面所说的优化策略中，节点有可能是从前面对比，也有可能是从后面对比，对比成功就会进行更新处理，也就是说我们有可能处理第一个，也有可能处理最后一个，那么我们在循环的时候就不能简单从前往后或从后往前循环，而是要从两边向中间循环。

那么该如何从两边向中间循环呢？请看下图： 

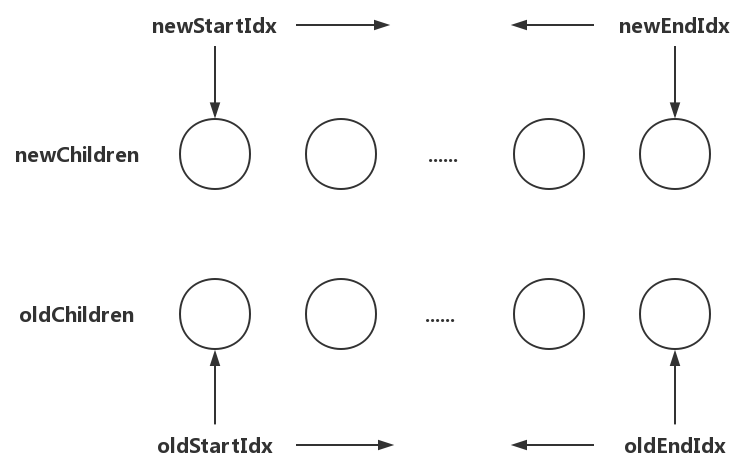
首先，我们先准备4个变量：

• newStartIdx:newChildren数组里开始位置的下标；
• newEndIdx:newChildren数组里结束位置的下标；
• oldStartIdx:oldChildren数组里开始位置的下标；
• oldEndIdx:oldChildren数组里结束位置的下标；

在循环的时候，每处理一个节点，就将下标向图中箭头所指的方向移动一个位置，开始位置所表示的节点被处理后，就向后移动一个位置；结束位置所表示的节点被处理后，就向前移动一个位置；由于我们的优化策略都是新旧节点两两更新的，所以一次更新将会移动两个节点。说的再直白一点就是：newStartIdx和oldStartIdx只能往后移动（只会加），newEndIdx和oldEndIdx只能往前移动（只会减）。

当开始位置大于结束位置时，表示所有节点都已经遍历过了。

OK，有了这个概念后，我们开始读源码：

1. 如果oldStartVnode不存在，则直接跳过，将oldStartIdx加1，比对下一个

   // 以"新前"、"新后"、"旧前"、"旧后"的方式开始比对节点
   while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
   	if (isUndef(oldStartVnode)) {
           oldStartVnode = oldCh[++oldStartIdx]
         }
   }
   

2. 如果oldEndVnode不存在，则直接跳过，将oldEndIdx减1，比对前一个

   else if (isUndef(oldEndVnode)) {
       oldEndVnode = oldCh[--oldEndIdx]
   }
   

3. 如果新前与旧前节点相同，就把两个节点进行patch更新，同时oldStartIdx和newStartIdx都加1，后移一个位置

   else if (sameVnode(oldStartVnode, newStartVnode)) {
       patchVnode(oldStartVnode, newStartVnode, insertedVnodeQueue)
       oldStartVnode = oldCh[++oldStartIdx]
       newStartVnode = newCh[++newStartIdx]
   }
   

4. 如果新后与旧后节点相同，就把两个节点进行patch更新，同时oldEndIdx和newEndIdx都减1，前移一个位置

   else if (sameVnode(oldEndVnode, newEndVnode)) {
       patchVnode(oldEndVnode, newEndVnode, insertedVnodeQueue)
       oldEndVnode = oldCh[--oldEndIdx]
       newEndVnode = newCh[--newEndIdx]
   }
   

5. 如果新后与旧前节点相同，先把两个节点进行patch更新，然后把旧前节点移动到oldChilren中所有未处理节点之后，最后把oldStartIdx加1，后移一个位置，newEndIdx减1，前移一个位置

   else if (sameVnode(oldStartVnode, newEndVnode)) {
       patchVnode(oldStartVnode, newEndVnode, insertedVnodeQueue)
       canMove && nodeOps.insertBefore(parentElm, oldStartVnode.elm, nodeOps.nextSibling(oldEndVnode.elm))
       oldStartVnode = oldCh[++oldStartIdx]
       newEndVnode = newCh[--newEndIdx]
   }
   

6. 如果新前与旧后节点相同，先把两个节点进行patch更新，然后把旧后节点移动到oldChilren中所有未处理节点之前，最后把newStartIdx加1，后移一个位置，oldEndIdx减1，前移一个位置

   else if (sameVnode(oldEndVnode, newStartVnode)) { // Vnode moved left
       patchVnode(oldEndVnode, newStartVnode, insertedVnodeQueue)
       canMove && nodeOps.insertBefore(parentElm, oldEndVnode.elm, oldStartVnode.elm)
       oldEndVnode = oldCh[--oldEndIdx]
       newStartVnode = newCh[++newStartIdx]
   }
   

7. 如果不属于以上四种情况，就进行常规的循环比对patch

8. 如果在循环中，oldStartIdx大于oldEndIdx了，那就表示oldChildren比newChildren先循环完毕，那么newChildren里面剩余的节点都是需要新增的节点，把[newStartIdx, newEndIdx]之间的所有节点都插入到DOM中

   if (oldStartIdx > oldEndIdx) {
       refElm = isUndef(newCh[newEndIdx + 1]) ? null : newCh[newEndIdx + 1].elm
       addVnodes(parentElm, refElm, newCh, newStartIdx, newEndIdx, insertedVnodeQueue)
   }
   

9. 如果在循环中，newStartIdx大于newEndIdx了，那就表示newChildren比oldChildren先循环完毕，那么oldChildren里面剩余的节点都是需要删除的节点，把[oldStartIdx, oldEndIdx]之间的所有节点都删除

   else if (newStartIdx > newEndIdx) {
       removeVnodes(parentElm, oldCh, oldStartIdx, oldEndIdx)
   }
   

OK,处理完毕，可见源码中的处理逻辑跟我们之前分析的逻辑是一样的。

8. 总结

本篇文章中，我们介绍了Vue中子节点更新的优化策略，发现Vue为了避免双重循环数据量大时间复杂度升高带来的性能问题，而选择了从子节点数组中的4个特殊位置互相比对，分别是：新前与旧前，新后与旧后，新后与旧前，新前与旧后。对于每一种情况我们都通过图文的形式对其逻辑进行了分析。最后我们回到源码，通过阅读源码来验证我们分析的是否正确。幸运的是我们之前每一步的分析都在源码中找到了相应的实现，得以验证我们的分析没有错。以上就是Vue中的patch过程，即DOM-Diff算法所有内容了，到这里相信你再读这部分源码的时候就有比较清晰的思路了。