CSP-202112-2-序列查询新解

【70分思路】

• 【暴力枚举】按照题目思路遍历一遍f(x)和g(x)，计算error(A)，时间复杂度为O(N)，时间超限。

#include <iostream>
using namespace std;
int main() {
    long long n, N, sum = 0;
    cin >> n >> N;
    long long r = N / (n + 1);
    long long* A = new long long[n + 1];
    A[0] = 0;

    for (int i = 1; i <= n; i++)
        cin >> A[i];

    // 初始化fx,gx
    int ii = 1;
    for (int i = 0; i < N; i++)
    {
        if (i == A[ii]) ii++;
        // abs((ii - 1) - (i / r)): |f(x) - g(x)|
        sum += abs((ii - 1) - (i / r));
    }
    cout << sum;

    delete[] A;
    return 0;
}

【100分思路】

• 【优化思路】结合第一问的提示，针对划分出的区间直接求解，似乎为该题的可行思路。
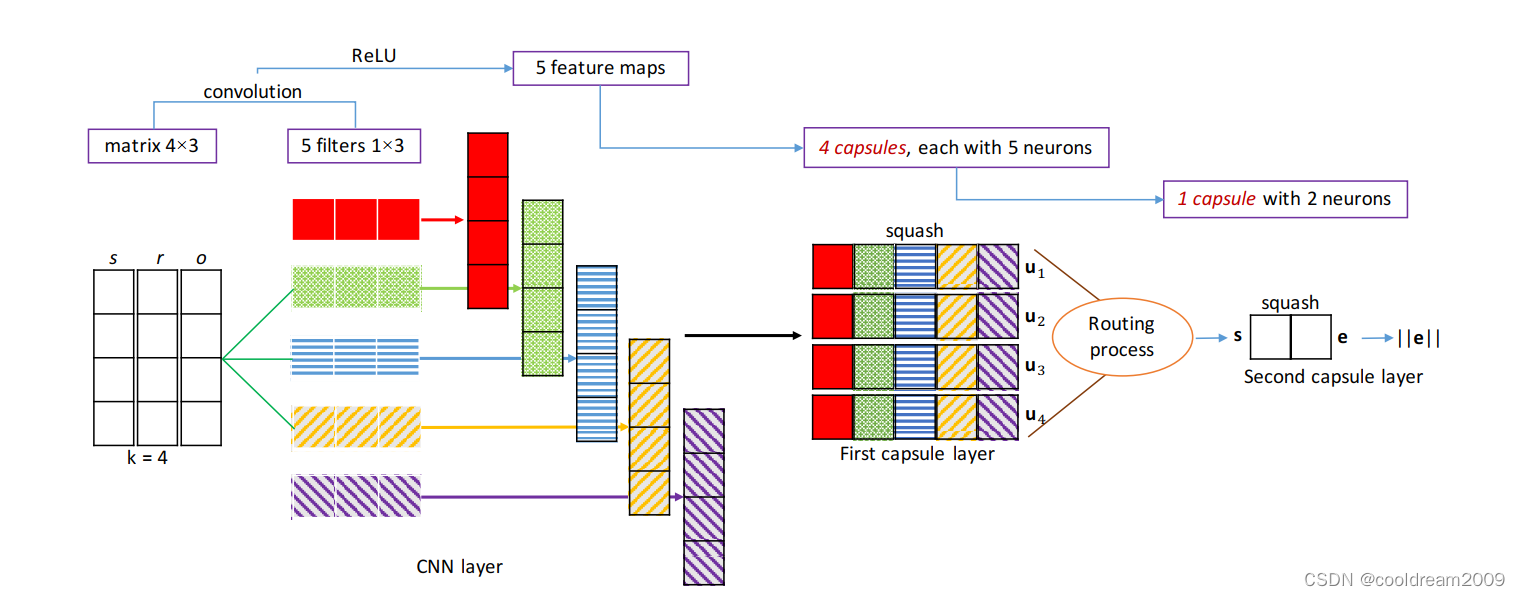
  • f(x)：求其在某个区间的和，可以直接借鉴第一题方法。在 $x\in [A[i-1],A[I])$ 时，所有的 f(x) 都为 $i-1$。
  • g(x)：g(x) 在确定的 f(x) 恒等区间里，其未必全部相等。但由于向下取整的运算，g(x) 也存在区间恒等的性质。因此在 f(x) 与 g(x) 的恒等区间重合部分就可以进行直接求解。
  • MAX 是仍与当前 g(x) 相等的最大 x （j==x）值，以此可求得对应 g(x) 恒等区间的长度 len。注意 MAX 的运算是可能超出当前 j 的恒等区间的，要确保不超过当前区间的边界。
  • len是确保|f(j) - g(j)| != 0的区间长度，并且在该区间内 |f(j) - g(j)| 恒等，该区间内的error(A)可以直接通过 (|f(j) - g(j)| * len计算。

#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
    int n, N, len, MAX = -1, A[100010] = {}; // MAX 仍与当前 g 相等的最大 j 值
    long long errorA = 0;
    cin >> n >> N;
    for (int i = 1; i <= n; i++)
    {
        cin >> A[i];
    }
    A[n + 1] = N;
    int r = N / (n + 1);    

    for (int i = 1; i <= n + 1; i++)
    {
        for (int j = A[i - 1]; j < A[i]; j += len)
        {
            int g = j / r; // j = x     
            //  (g + 1) * r - 1 是 MAX 可能的最大值，确保不超过当前区间的边界
            if ((g + 1) * r - 1 < A[i]) {
                MAX = (g + 1) * r - 1;
            }
            else {
                MAX = A[i] - 1;
            }
            len = MAX - j + 1; 
            errorA += (abs(i - 1 - g)) * len; // f(x) = i - 1
        }
    }
    cout << errorA;
    return 0;
}