本文记录了BFM算法代码在windows上的安装过程。
算法原网站:https://wasserstein-gradient-flows.netlify.app/
github:https://github.com/wonjunee/wgfBFMcodes
文章目录
- FFTW
- wgfBFMcodes
- MATLAB
- python
- 注
FFTW
官网/下载路径:https://www.fftw.org/install/windows.html
windows下FFTW安装教程可参考:
- https://blog.csdn.net/Jhon_ranble/article/details/120576590
- https://blog.csdn.net/ifenghua135792468/article/details/80608138?utm_medium=distribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-0-80608138-blog-70225210.235v43pc_blog_bottom_relevance_base9&spm=1001.2101.3001.4242.1&utm_relevant_index=3
下载并解压,之后使用VS编译。
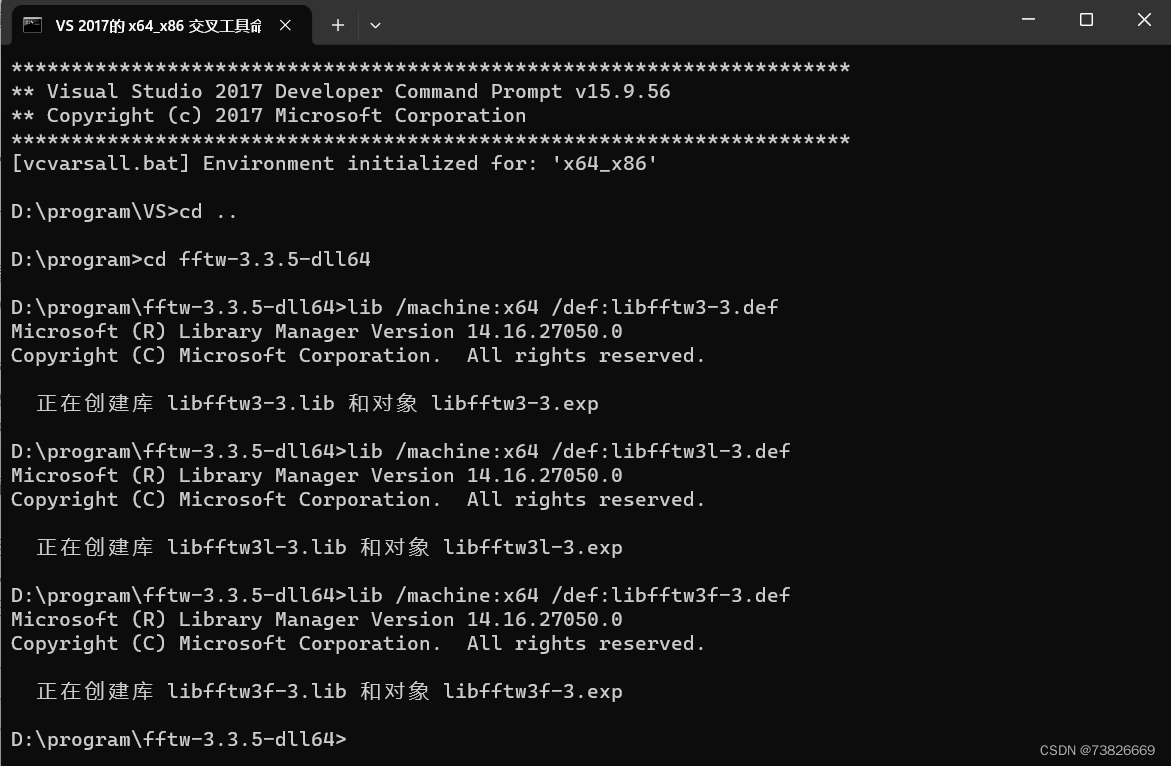
本人采用VS2017,“x86 Native Tools Command Prompt for VS 2017”和“VS 2017的 x64_x86 交叉工具命令提示符”都可以。打开后cd到fftw解压路径,输入以下三个命令
lib /machine:x64 /def:libfftw3-3.def
lib /machine:x64 /def:libfftw3l-3.def
lib /machine:x64 /def:libfftw3f-3.def
结束后如图:
将生成的libfftw3-3.dll, libfftw3-3f.dll, libfftw3-3l.dll放入Windows/System32中,然后将生成的库文件libfftw3-3.lib libfftw3f-3.lib libfftw3l-3.lib放入VS中的lib文件夹,把fftw3.h放入include文件夹。
wgfBFMcodes
下载github上的源码,可用git命令clone
git clone https://github.com/wonjunee/wgfBFMcodes
cd wgfBFMcodes/
MATLAB
从github clone代码后,用matlab打开,用mex命令编译。mex命令可以参考https://ww2.mathworks.cn/help/matlab/ref/mex.html#btw193f-1
在交互窗口输入
mex -setup C++
mex COMPFLAGS='$COMPFLAGS -std=c++17' src/wgfslow.cpp
mex COMPFLAGS='$COMPFLAGS -std=c++17' src/wgfinc.cpp
目前仍有报错,以后再修改。
python
打开cmd,cd到wgfBFMcodes/python下,运行compile.sh。此时程序会根据你电脑中的C/C++编译器编译src文件夹下的文件来获得接口。
注
可能我电脑上的C的编译器比较混乱,出现了M_PI没有定义的报错。在报错的文件添加
#define M_PI 3.14159265358979323846
即可运行。