1 相遇数

相遇数（Rencontres Number，partial derangement numbers）是指部分扰动的数量，或与独立对象的r相遇的置换数（即具有固定点的独立对象的置换数）。

看不通。懂的朋友给解释一下哈。

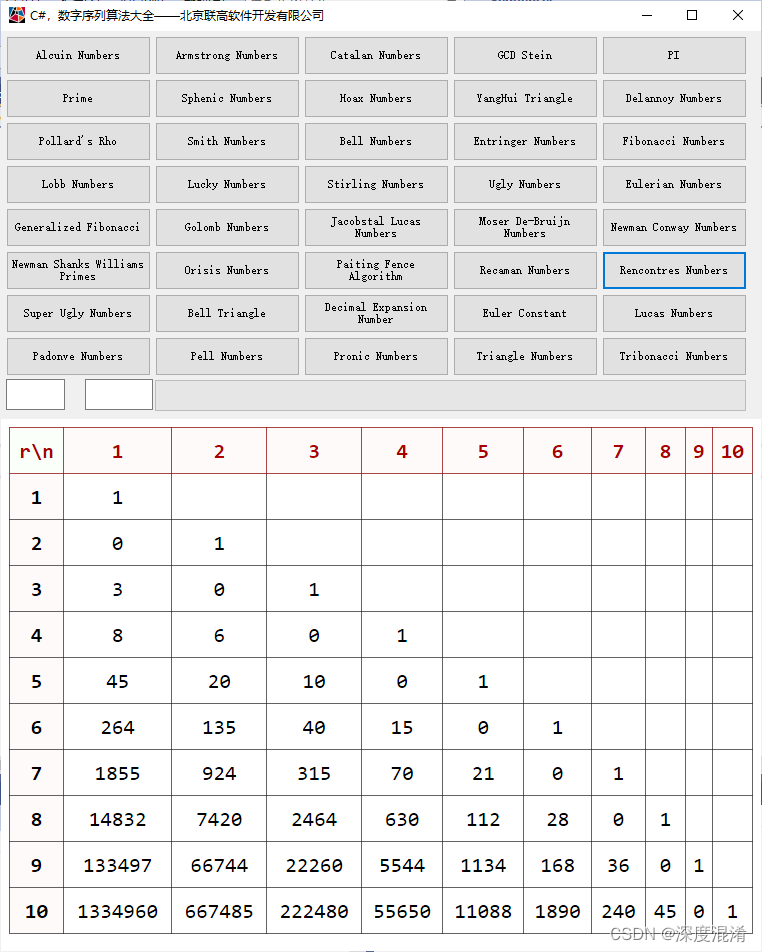
2 源程序

using System;

namespace Legalsoft.Truffer.Algorithm
{
    public static partial class Number_Sequence
    {
        private static int Rencontres_Number_Binomial_Coeff(int n, int k)
        {
            if (k == 0 || k == n)
            {
                return 1;
            }
            return Rencontres_Number_Binomial_Coeff(n - 1, k - 1) + Rencontres_Number_Binomial_Coeff(n - 1, k);
        }
        
        public static int Rencontres_Number(int n, int m)
        {
            if (n == 0 && m == 0)
            {
                return 1;
            }
            if (n == 1 && m == 0)
            {
                return 0;
            }
            if (m == 0)
            {
                return (n - 1) * (Rencontres_Number(n - 1, 0) + Rencontres_Number(n - 2, 0));
            }
            return Rencontres_Number_Binomial_Coeff(n, m) * Rencontres_Number(n - m, 0);
        }

        private static int[,] Rencontres_Number_Binomial_Coeff_Second(int n, int k)
        {
            int[,] Coeff = new int[MAX, MAX];
            for (int i = 0; i <= n; i++)
            {
                for (int j = 0; j <= Math.Min(i, k); j++)
                {
                    if (j == 0 || j == i)
                    {
                        Coeff[i, j] = 1;
                    }
                    else
                    {
                        Coeff[i, j] = Coeff[i - 1, j - 1] + Coeff[i - 1, j];
                    }
                }
            }
            return Coeff;
        }

        public static int Rencontres_Number_Second(int n, int m)
        {
            int[,] Coeff = Rencontres_Number_Binomial_Coeff_Second(n, m);
            int[,] dp = new int[n + 1, m + 1];
            for (int i = 0; i <= n; i++)
            {
                for (int j = 0; j <= m; j++)
                {
                    if (j <= i)
                    {
                        if (i == 0 && j == 0)
                        {
                            dp[i, j] = 1;
                        }
                        else if (i == 1 && j == 0)
                        {
                            dp[i, j] = 0;
                        }
                        else if (j == 0)
                        {
                            dp[i, j] = (i - 1) * (dp[i - 1, 0] + dp[i - 2, 0]);
                        }
                        else
                        {
                            dp[i, j] = Coeff[i, j] * dp[i - j, 0];
                        }
                    }
                }
            }
            return dp[n, m];
        }
    }
}
 

——————————————————————————

POWER BY TRUFFER.CN 50018.COM

3 代码格式

using System;

namespace Legalsoft.Truffer.Algorithm
{
    public static partial class Number_Sequence
    {
        private static int Rencontres_Number_Binomial_Coeff(int n, int k)
        {
            if (k == 0 || k == n)
            {
                return 1;
            }
            return Rencontres_Number_Binomial_Coeff(n - 1, k - 1) + Rencontres_Number_Binomial_Coeff(n - 1, k);
        }
        
        public static int Rencontres_Number(int n, int m)
        {
            if (n == 0 && m == 0)
            {
                return 1;
            }
            if (n == 1 && m == 0)
            {
                return 0;
            }
            if (m == 0)
            {
                return (n - 1) * (Rencontres_Number(n - 1, 0) + Rencontres_Number(n - 2, 0));
            }
            return Rencontres_Number_Binomial_Coeff(n, m) * Rencontres_Number(n - m, 0);
        }

        private static int[,] Rencontres_Number_Binomial_Coeff_Second(int n, int k)
        {
            int[,] Coeff = new int[MAX, MAX];
            for (int i = 0; i <= n; i++)
            {
                for (int j = 0; j <= Math.Min(i, k); j++)
                {
                    if (j == 0 || j == i)
                    {
                        Coeff[i, j] = 1;
                    }
                    else
                    {
                        Coeff[i, j] = Coeff[i - 1, j - 1] + Coeff[i - 1, j];
                    }
                }
            }
            return Coeff;
        }

        public static int Rencontres_Number_Second(int n, int m)
        {
            int[,] Coeff = Rencontres_Number_Binomial_Coeff_Second(n, m);
            int[,] dp = new int[n + 1, m + 1];
            for (int i = 0; i <= n; i++)
            {
                for (int j = 0; j <= m; j++)
                {
                    if (j <= i)
                    {
                        if (i == 0 && j == 0)
                        {
                            dp[i, j] = 1;
                        }
                        else if (i == 1 && j == 0)
                        {
                            dp[i, j] = 0;
                        }
                        else if (j == 0)
                        {
                            dp[i, j] = (i - 1) * (dp[i - 1, 0] + dp[i - 2, 0]);
                        }
                        else
                        {
                            dp[i, j] = Coeff[i, j] * dp[i - j, 0];
                        }
                    }
                }
            }
            return dp[n, m];
        }
    }
}