---

N-Gram 模型

N-Gram 模型的构建过程如下：

1.将给定的文本分割成连续的N个词的组合(N-Gram)

比如，在Bigram 模型(2-Gram 模型，即二元模型)中，我们将文本分割成多个由相邻的两个词构成的组合，称它们为“二元组”(2-Gram )。

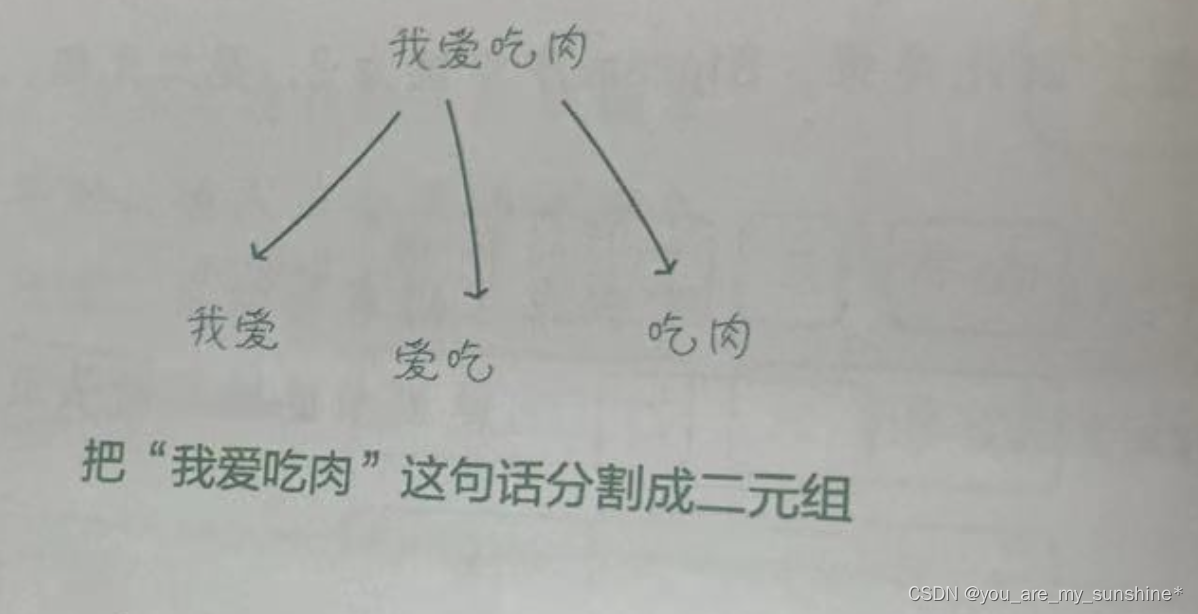
2.统计每个N-Gram在文本中出现的次数，也就是词频

比如，二元组“我爱”在语料库中出现了3次(如下页图所示)，即这个二元组的词频为3。

3.为了得到一个词在给定上下文中出现的概率，我们可以利用条件概率公式计算。具体来讲，就是计算给定前N-1个词时，下一个词出现的概率。这个概率可以通过计算某个N-Gram出现的次数与前N-1个词(前缀)出现的次数之比得到

比如，二元组“我爱”在语料库中出现了3次，而二元组的前缀“我”在语料库中出现了10次，则给定“我”，下一个词为“爱”的概率为30%(如下图所示)。

4.可以使用这些概率来预测文本中下一个词出现的可能性。多次迭代这个过程，甚至可以生成整个句子，也可以算出每个句子在语料库中出现的概率

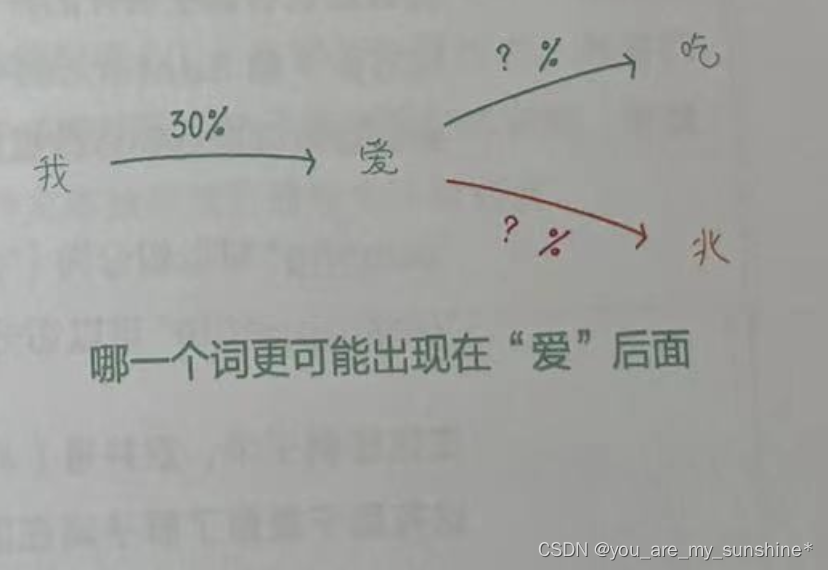
比如，从一个字“我”，生成“爱”，再继续生吃
成“吃”，直到“我爱吃肉”这个句子。计算“我爱”“爱吃”“吃肉”出现的概率，然后乘以各自的条件概率，就可以得到这个句子在语料库中出现的概率了。如上图所示。

“词”是什么，如何“分词”

在N-Gram 模型中，它表示文本中的一个元素，“N-Gram”指长度为N的连续元素序列。

这里的“元素”在英文中可以指单词，也可以指字符，有时还可以指“子词”(Subword );而在中文中，可以指词或者短语，也可以指字。

一般的自然语言处理工具包都为我们提供好了分词的工具。比如，英文分词通常使用 NLTK、spaCy等自然语言处理库，中文分词通常使用jieba库(中文NLP工具包)，而如果你将来会用到BERT这样的预训 I练模型，那么你就需要使用BERT 的专属分词器Tokenizer，它会把每个单词拆成子词一这是 BERT处理生词的方法。

创建一个Bigram字符预测模型

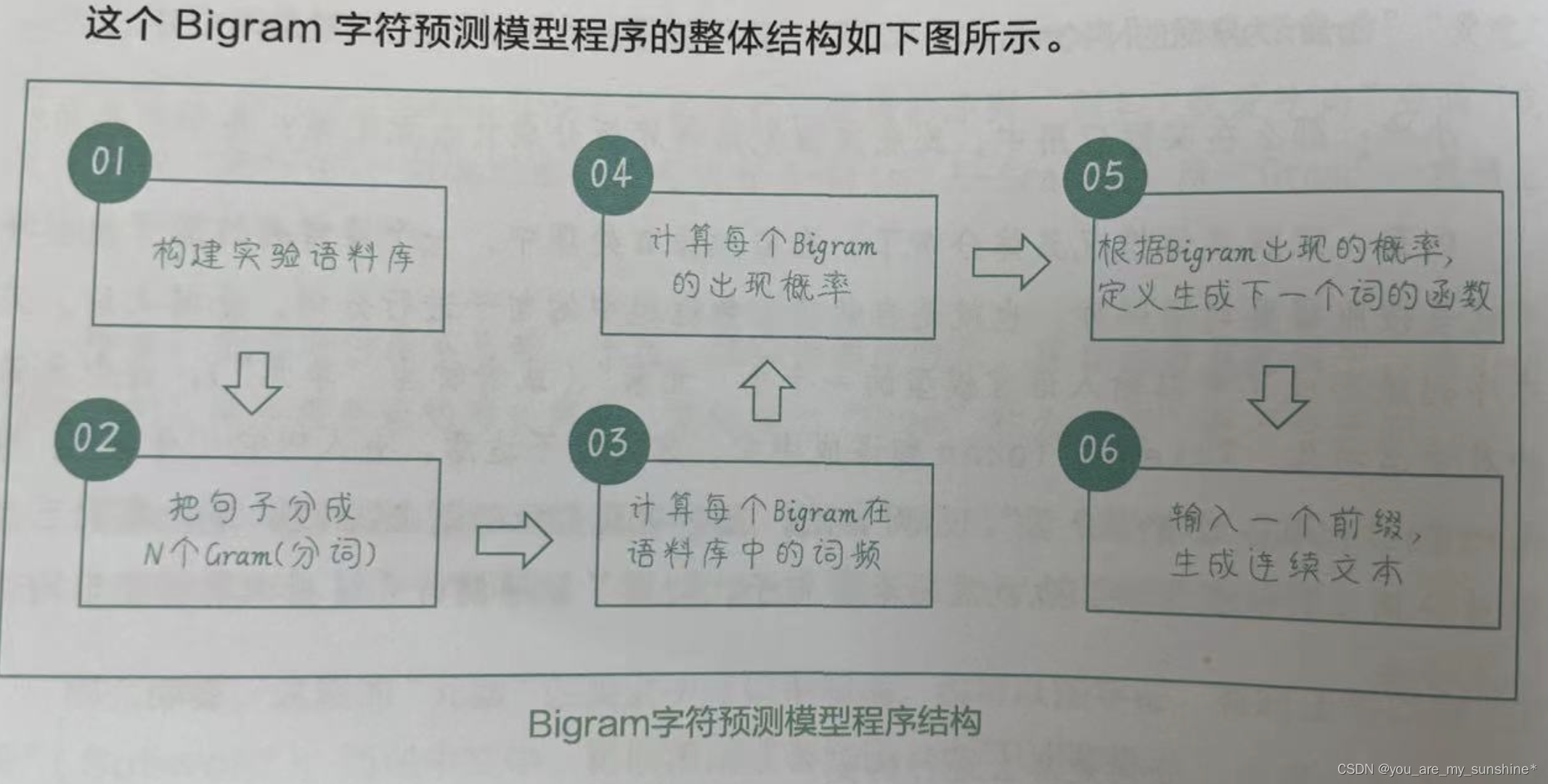
1.构建实验语料库

# 构建一个数据集
corpus = ["小张每天喜欢学习",
          "小张周末喜欢徒步",
          "小李工作日喜欢加班",
          "小李周末喜欢爬山",
          "小张周末喜欢爬山",
          "小李不喜欢躺平"]

2.把句子分成N个Gram(分词)

# 定义一个分词函数，将文本转换为单个字符的列表
def tokenize(text):
    return [char for char in text] # 将文本拆分为字符列表
# 对每个文本进行分词，并打印出对应的单字列表
print("单字列表:") 
for text in corpus:
    tokens = tokenize(text)
    print(tokens)

3.计算每个Bigram在语料库中的词频

# 定义计算 N-Gram 词频的函数
from collections import defaultdict, Counter # 导入所需库
def count_ngrams(corpus, n):
    ngrams_count = defaultdict(Counter)  # 创建一个字典，存储 N-Gram 计数
    for text in corpus:  # 遍历语料库中的每个文本
        tokens = tokenize(text)  # 对文本进行分词
        for i in range(len(tokens) - n + 1):  # 遍历分词结果，生成 N-Gram
            ngram = tuple(tokens[i:i+n])  # 创建一个 N-Gram 元组
            prefix = ngram[:-1]  # 获取 N-Gram 的前缀
            token = ngram[-1]  # 获取 N-Gram 的目标单字
            ngrams_count[prefix][token] += 1  # 更新 N-Gram 计数
    return ngrams_count
bigram_counts = count_ngrams(corpus, 2) # 计算 bigram 词频
print("bigram 词频：") # 打印 bigram 词频
for prefix, counts in bigram_counts.items():
    print("{}: {}".format("".join(prefix), dict(counts))) 

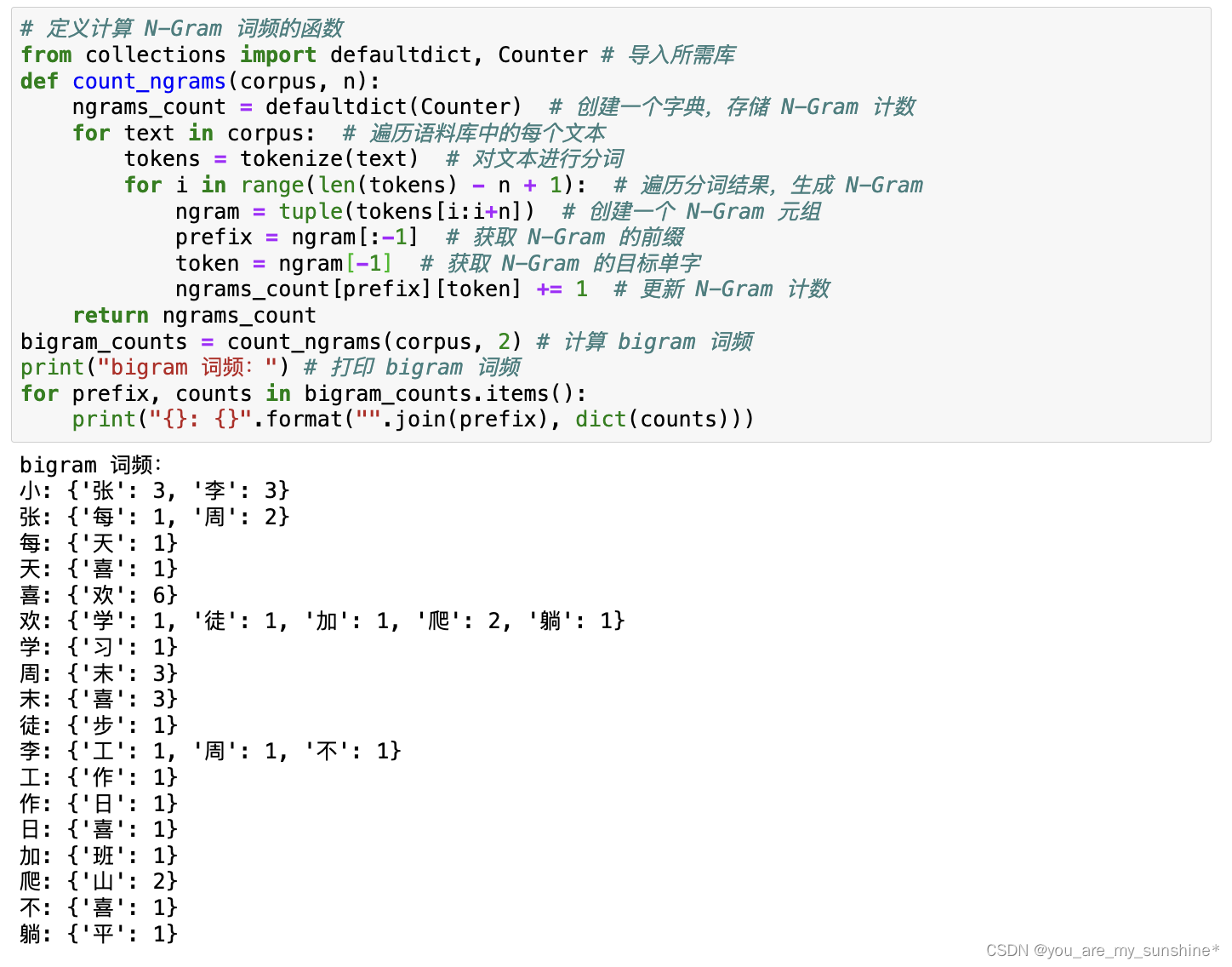
4.计算每个Bigram的出现概率

# 定义计算 N-Gram 出现概率的函数
def ngram_probabilities(ngram_counts):
    ngram_probs = defaultdict(Counter) # 创建一个字典，存储 N-Gram 出现的概率
    for prefix, tokens_count in ngram_counts.items(): # 遍历 N-Gram 前缀
        total_count = sum(tokens_count.values()) # 计算当前前缀的 N-Gram 计数
        for token, count in tokens_count.items(): # 遍历每个前缀的 N-Gram
            ngram_probs[prefix][token] = count / total_count # 计算每个 N-Gram 出现的概率
    return ngram_probs
bigram_probs = ngram_probabilities(bigram_counts) # 计算 bigram 出现的概率
print("\nbigram 出现的概率 :") # 打印 bigram 概率
for prefix, probs in bigram_probs.items():
    print("{}: {}".format("".join(prefix), dict(probs)))

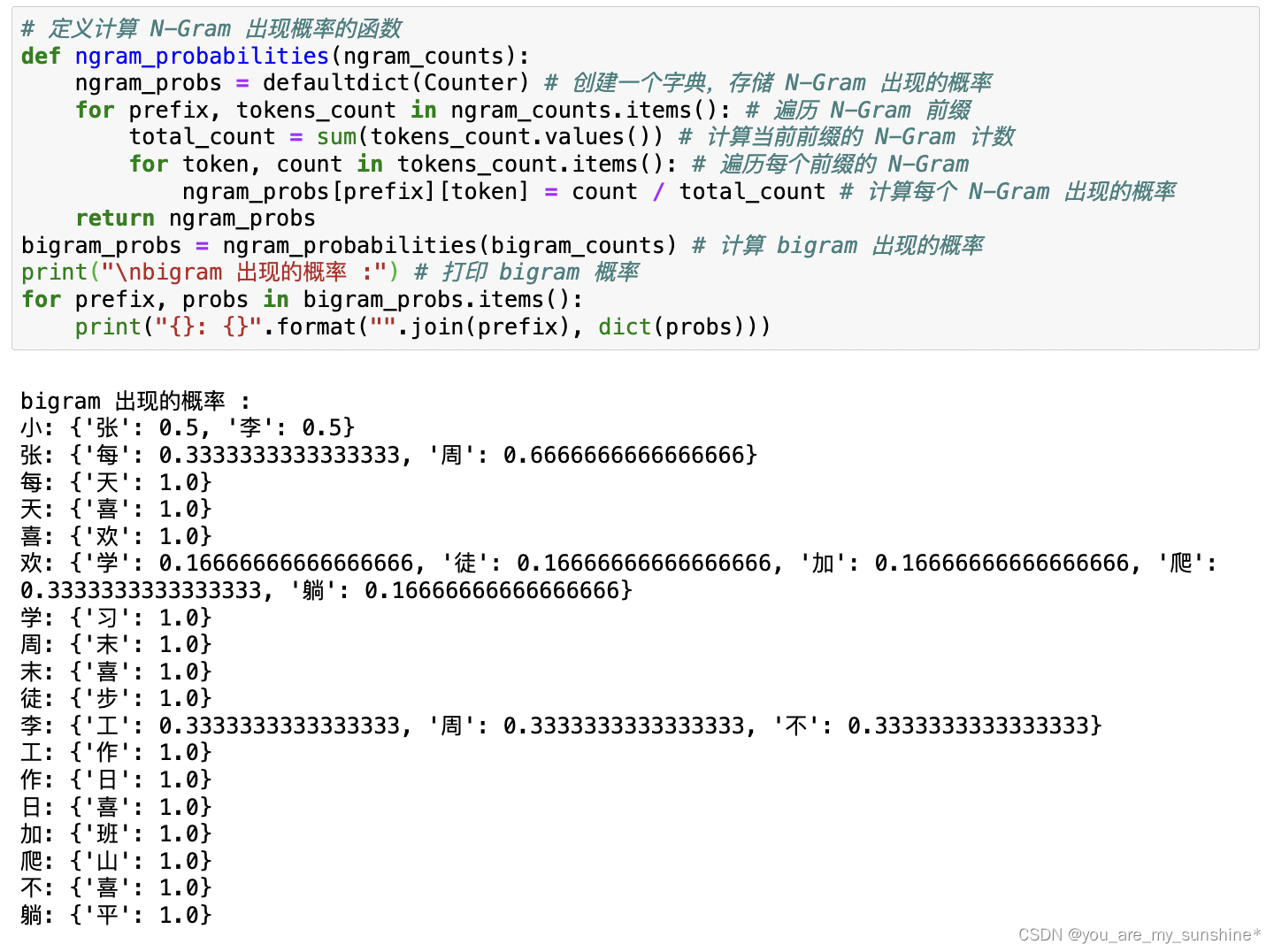
5.根据Bigram出现的概率，定义生成下一个词的函数

# 定义生成下一个词的函数
def generate_next_token(prefix, ngram_probs):
    if not prefix in ngram_probs: # 如果前缀不在 N-Gram 中，返回 None
        return None
    next_token_probs = ngram_probs[prefix] # 获取当前前缀的下一个词的概率
    next_token = max(next_token_probs, 
                    key=next_token_probs.get) # 选择概率最大的词作为下一个词
    return next_token

6.输入一个前缀，生成连续文本

# 定义生成连续文本的函数
def generate_text(prefix, ngram_probs, n, length=8):
    tokens = list(prefix) # 将前缀转换为字符列表
    for _ in range(length - len(prefix)): # 根据指定长度生成文本 
    # 获取当前前缀的下一个词
        next_token = generate_next_token(tuple(tokens[-(n-1):]), ngram_probs) 
        if not next_token: # 如果下一个词为 None，跳出循环
            break
        tokens.append(next_token) # 将下一个词添加到生成的文本中
    return "".join(tokens) # 将字符列表连接成字符串

# 输入一个前缀，生成文本
generated_text = generate_text("小", bigram_probs, 2)
print("\n 生成的文本：", generated_text) # 打印生成的文本

N-Gram 模型小结

N-Gram 是一种用于语言建模的技术，它用来估计文本中词序列的概率分布。 N-Gram 模型将文本看作一个由词序列构成的随机过程，根据已有的文本数据，计算出词序列出现的概率。因此，N-Gram主要用于语言建模、文本生成、语音识别等自然语言处理任务中。

• (1)N-Gram是一种基于连续词序列的文本表示方法。它将文本分割成由连续的 N个词组成的片段，从而捕捉局部语序信息。
• (2)N-Gram 可以根据不同的N值捕捉不同程度的上下文信息。例如，1-Gram(Unigram)仅关注单个词，而2-Gram(Bigram)关注相邻的两个词的组合，以此类推。
• (3)随着N的增加，模型可能会遇到数据稀疏性问题，导致模型性能下降。

---

学习的参考资料：
（1）书籍
利用Python进行数据分析
西瓜书
百面机器学习
机器学习实战
阿里云天池大赛赛题解析(机器学习篇)
白话机器学习中的数学
零基础学机器学习
图解机器学习算法

动手学深度学习（pytorch）

…

（2）机构
光环大数据
开课吧
极客时间
七月在线
深度之眼
贪心学院
拉勾教育
博学谷
慕课网
海贼宝藏
…