139.单词拆分

题目链接：139.单词拆分
文章讲解：代码随想录|139.单词拆分
视频讲解：139.单词拆分

思路

按照双指针思路直接想这题更好理解，用动态规划五部曲思考有点不好理解

代码

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
        vector<bool> dp(s.size() + 1, false);
        dp[0] = true;
        for(int i = 1; i <= s.size(); i++){
            for(int j = 0; j < i; j++){
                string word = s.substr(j, i - j);
                if(wordSet.find(word) != wordSet.end() && dp[j] == true){
                    dp[i] = true;
                }
            }
        }
        return dp[s.size()];
    }
};

多重背包

文章讲解：代码随想录|多重背包

思路

有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用，每件耗费的空间是Ci ，价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量，且价值总和最大。

多重背包和01背包是非常像的， 为什么和01背包像呢？

每件物品最多有Mi件可用，把Mi件摊开，其实就是一个01背包问题了。
例如：

背包最大重量为10。

物品为：

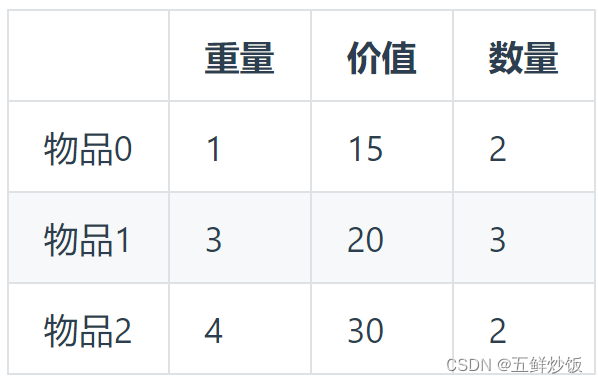
摊开：

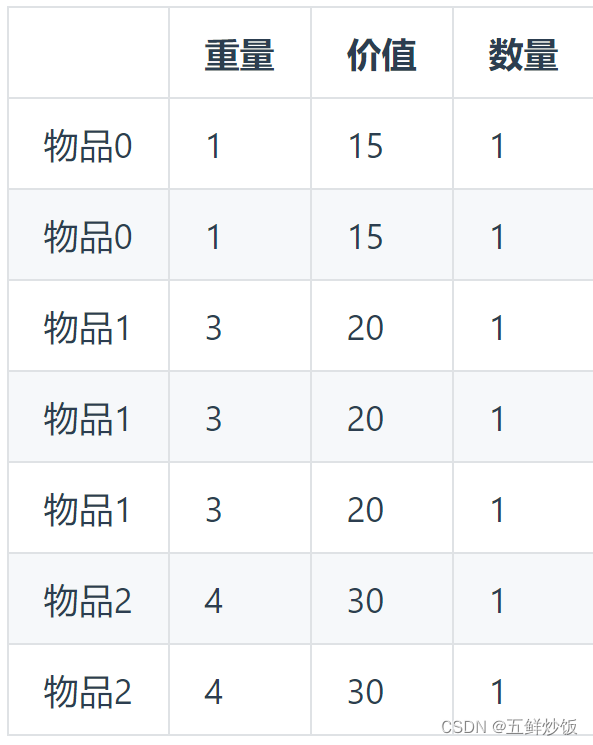
代码

#include<iostream>
#include<vector>
using namespace std;
int main() {
    int bagWeight,n;
    cin >> bagWeight >> n;
    vector<int> weight(n, 0);
    vector<int> value(n, 0);
    vector<int> nums(n, 0);
    for (int i = 0; i < n; i++) cin >> weight[i];
    for (int i = 0; i < n; i++) cin >> value[i];
    for (int i = 0; i < n; i++) cin >> nums[i];

    vector<int> dp(bagWeight + 1, 0);

    for(int i = 0; i < n; i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            // 以上为01背包，然后加一个遍历个数
            for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数
                dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);
            }
        }
    }

    cout << dp[bagWeight] << endl;
}

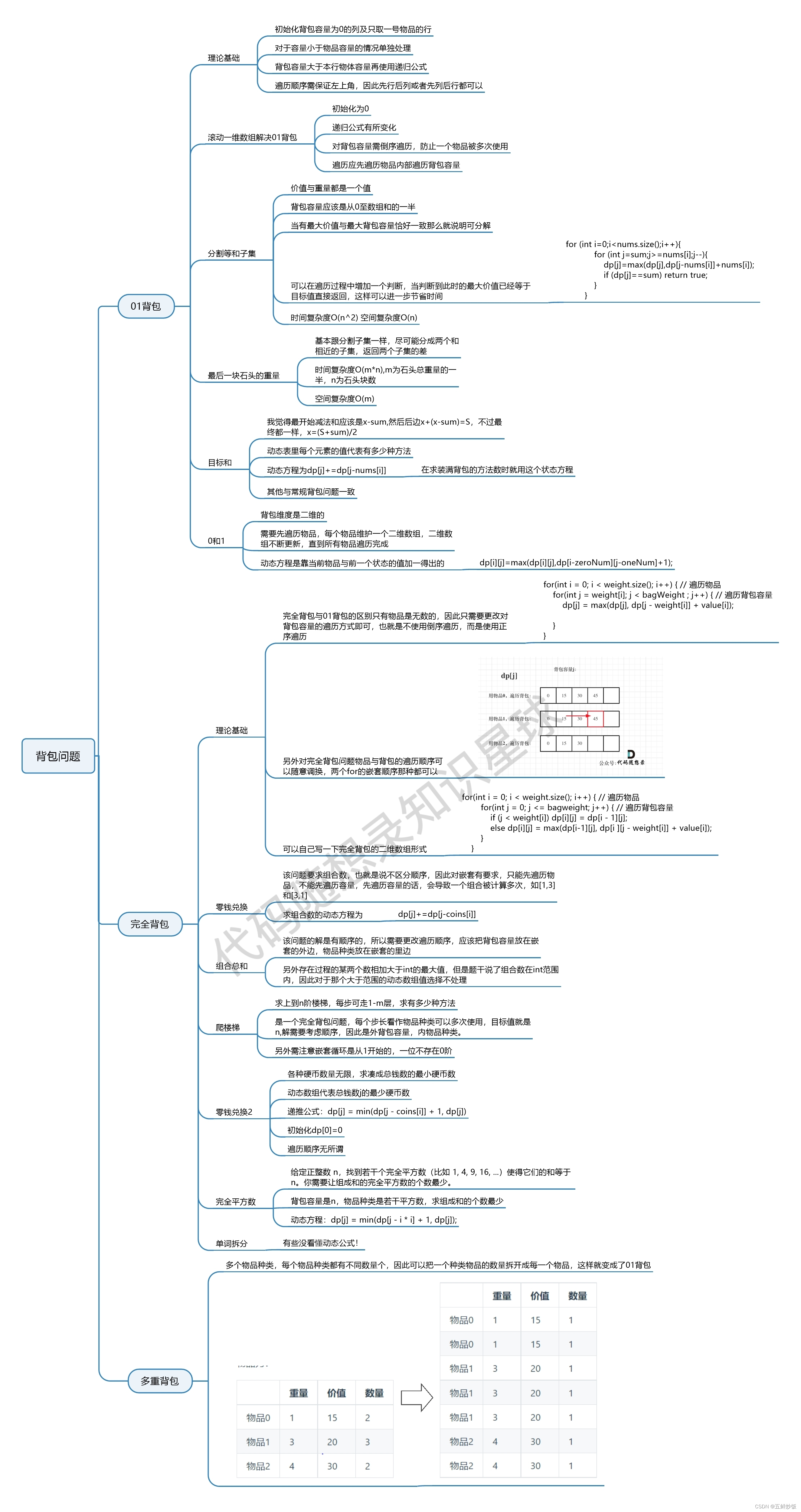
背包问题总结

文章讲解：代码随想录|背包问题总结

思路

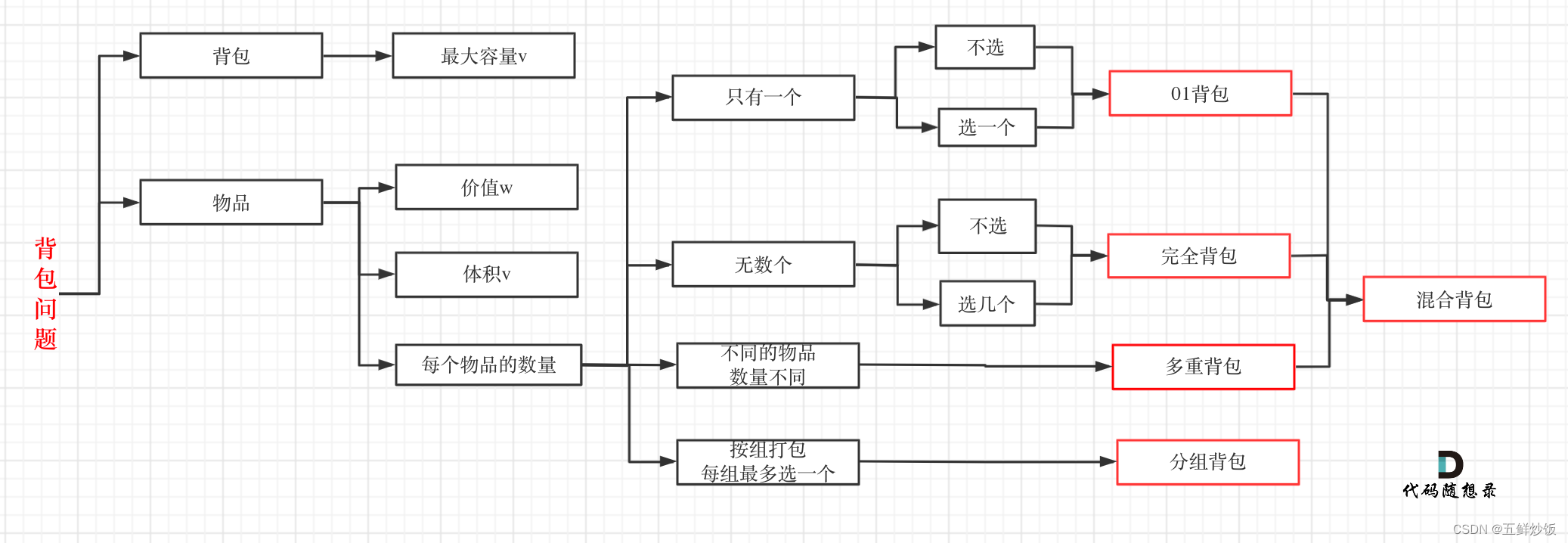
代码