目录
一、GM(1,1)模型预测原理
二、GM(1,1)模型预测步骤
2.1 数据的检验与处理
2.2 建立模型
2.3 检验预测值
三、案例
灰色预测应用场景:时间序列预测
灰色预测的主要特点是模型使用的不是原始数据序列,而是生成的数据序列。其核心体系是灰色模型,即对原始数据做累加生成得到近似的指数规律再进行建模的方法。
优点是不需要很多的数据,一般只需要4个数据就可以,能解决历史数据少、序列的完整性及可靠性低的问题;能利用微分方程来充分挖掘系统的本质,精度高;能将无规律的原始数据进行生成得到规律性较强的生成序列,运算简便,易于检验,具有不考虑分布规律,不考虑变化趋势。
缺点是只适用于中短期的预测,只适合指数增长的预测。
一、GM(1,1)模型预测原理

二、GM(1,1)模型预测步骤
2.1 数据的检验与处理

2.2 建立模型

2.3 检验预测值

三、案例
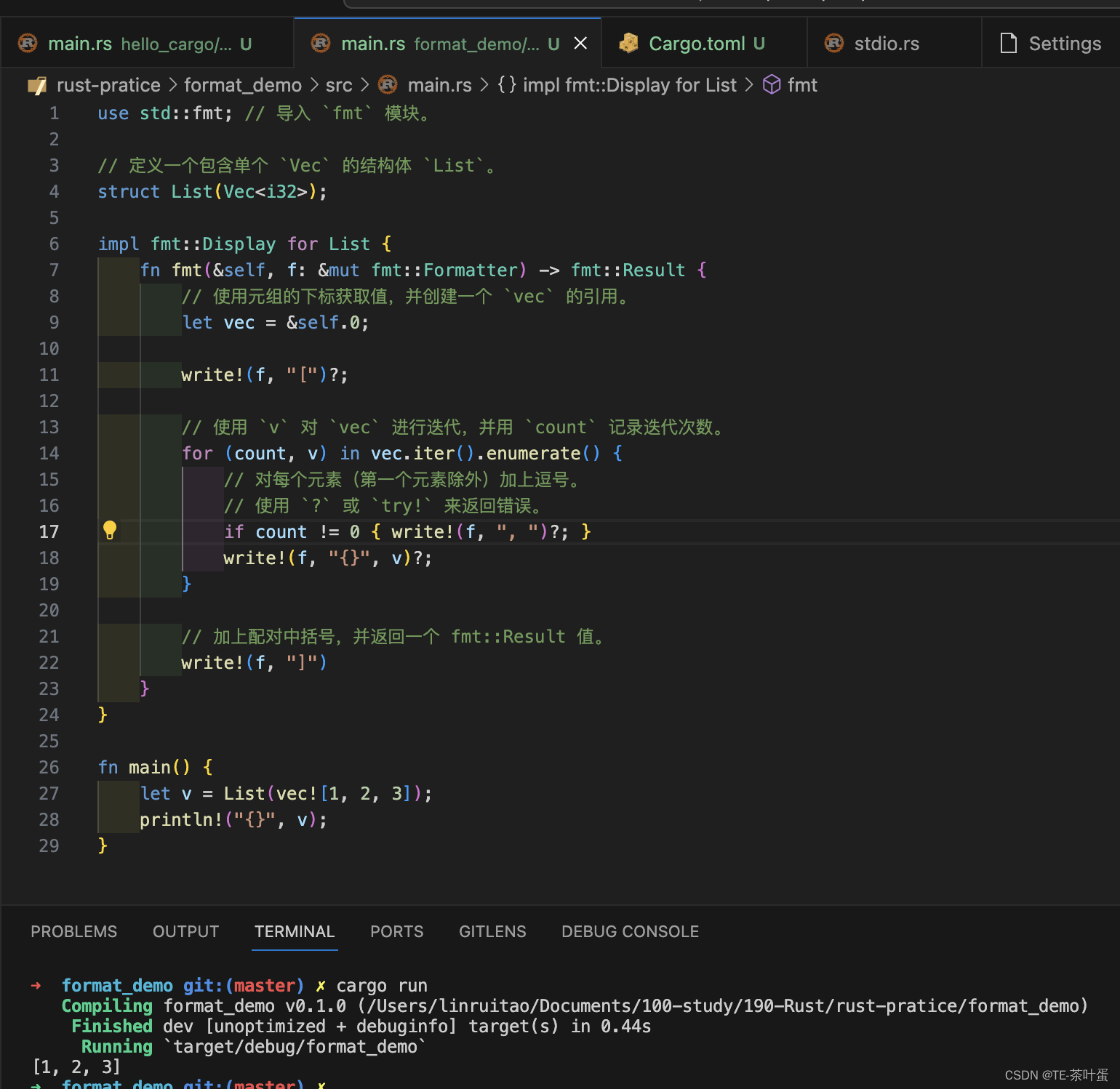
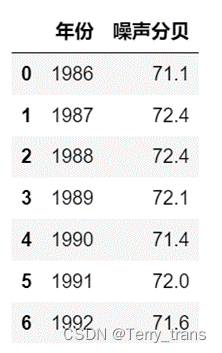
由北方某城市1986-1992年道路交通噪声平均值声级数据如表,进行未来10年的预测。
解:
级比检验
首先导入数据,做级比检验
import pandas as pd
import numpy as np
data = pd.read_excel(r"C:\Users\Terry\Desktop\城市交通噪声数据.xlsx")
x_0 = np.array(data["噪声分贝"].to_list()) # [1,2,3] ndarray
x_0# 级比检验
def level_ratio_test(x):
# 可容覆盖范围
n = len(x)
cover_range = [np.exp(-2/(n+1)), np.exp(2/(n+1))]
# 计算x[i]/x[i+1]的值,即计算级比
lambda_x = x[:-1] / x[1:]
for i in lambda_x:
if i < cover_range[0] or i > cover_range[1]:
print("不通过级比检验,无法使用GM(1,1)")
break
return
print("通过级比检验,可以使用GM(1,1)")
level_ratio_test(x_0)
![]()
注:这里直接写了一个函数,计算量可容覆盖范围,循环判断是每个数的级比是否满足要求,如果不满足,跳出循环,并输出无法使用GM(1,1),如果循环结束,仍然没有输出无法使用,则标明所有级比均通过检验可以输出“通过级比检验,可以使用GM(1,1)”
建模及预测
# 1.计算一次累加生成序列z_1
x_1 = x_0.cumsum()
# 2.计算均值生成序列z_1
z_1 = (x_1[:-1] + x_1[1:]) / 2.0
# 3.计算B矩阵
B = np.vstack([-z_1, np.ones(len(x_0)-1)]).T
# 4.计算Y矩阵
Y = x_0[1:].reshape((-1, 1))
# 5.计算a,b
# a为发展系数 b为灰色作用量
[[a], [b]] = np.linalg.inv(B.T @ B) @ B.T @ Y # 计算参数
# 6.原始年份的预测值
x_1_predict = []
n = len(x_0)
for k in range(n): # 如果预测k个未来年份 这里就n+k 假设预测未来5年就n+5
x_1_predict.append((x_0[0]-b/a)*np.exp(-a*k) + b/a)
# 7.还原数据
x_0_predict = np.hstack([x_0[0],np.diff(x_1_predict)])
结果检验
import pandas as pd
result = pd.DataFrame({"原始数据":x_0,
"预测数据":x_0_predict})
# 残差:真实值 - 预测值
result["残差"] = result["原始数据"] - result["预测数据"]
# 相对误差
result["相对误差"] = (abs(result["原始数据"] - result["预测数据"]) / result["原始数据"]).map('{:.2%}'.format)
# 级比偏差
lambda_x = x_0[:-1] / x_0[1:]
result["级比偏差值"] = np.append(np.nan, abs(1-(1-0.5*a)/(1+0.5*a)*lambda_x))
result

相对误差、级别偏差均小于0.1,达到较高要求。
结果描述及未来预测
通过绘制折线图来看真实值和预测值的比较
result = result.set_index(data.年份)
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 输出高清图像
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
#设定 seaborn 风格
sns.set()
with plt.xkcd():
#用 matplotlib 画出每个序列的折线
plt.figure(figsize=(10,6))
plt.plot(result['原始数据'], label='Original data',marker='o',color='g')
plt.plot(result['预测数据'], label='Predicted data',marker='X',color='r')
# 设定图例和标题
plt.legend()
plt.title('Comparison of Original Data and Predicted Data')
# 设置坐标轴范围
plt.ylim(60, 85)
# 显示图表
plt.show()
# 假设预测10年
x_1_predict = []
for k in range(n+10): # 如果预测k个未来年份 这里就n+k 假设预测未来5年就n+5
x_1_predict.append((x_0[0]-b/a)*np.exp(-a*k) + b/a) # 递推计算 第k+1个数 比如k=0的时候 就是第一个预测值
x_1_predict
# 7.还原数据
x_0_predict = np.hstack([x_0[0],np.diff(x_1_predict)])
x_0_predict
year = data["年份"].tolist()
for i in range(10):
year.append(year[-1]+1)
x_0_predict_more = pd.DataFrame({"未来预测":x_0_predict,"年份":year})
x_0_predict_more = x_0_predict_more.set_index("年份")
x_0_predict_more.iloc[0:n-1,:] = np.nan
with plt.xkcd():
#用 matplotlib 画出每个序列的折线
plt.figure(figsize=(10,6))
plt.plot(result['原始数据'], label='Original data',marker='o',color='g')
plt.plot(result['预测数据'], label='Predicted data',marker='X',color='r')
plt.plot(x_0_predict_more['未来预测'], label='Predicted Future data',marker='1',color='b',linestyle='--')
# 设定图例和标题
plt.legend()
plt.title('Comparison of Original Data and Predicted Data')
# 设置坐标轴范围
plt.ylim(60, 80)
# 显示图表
plt.show()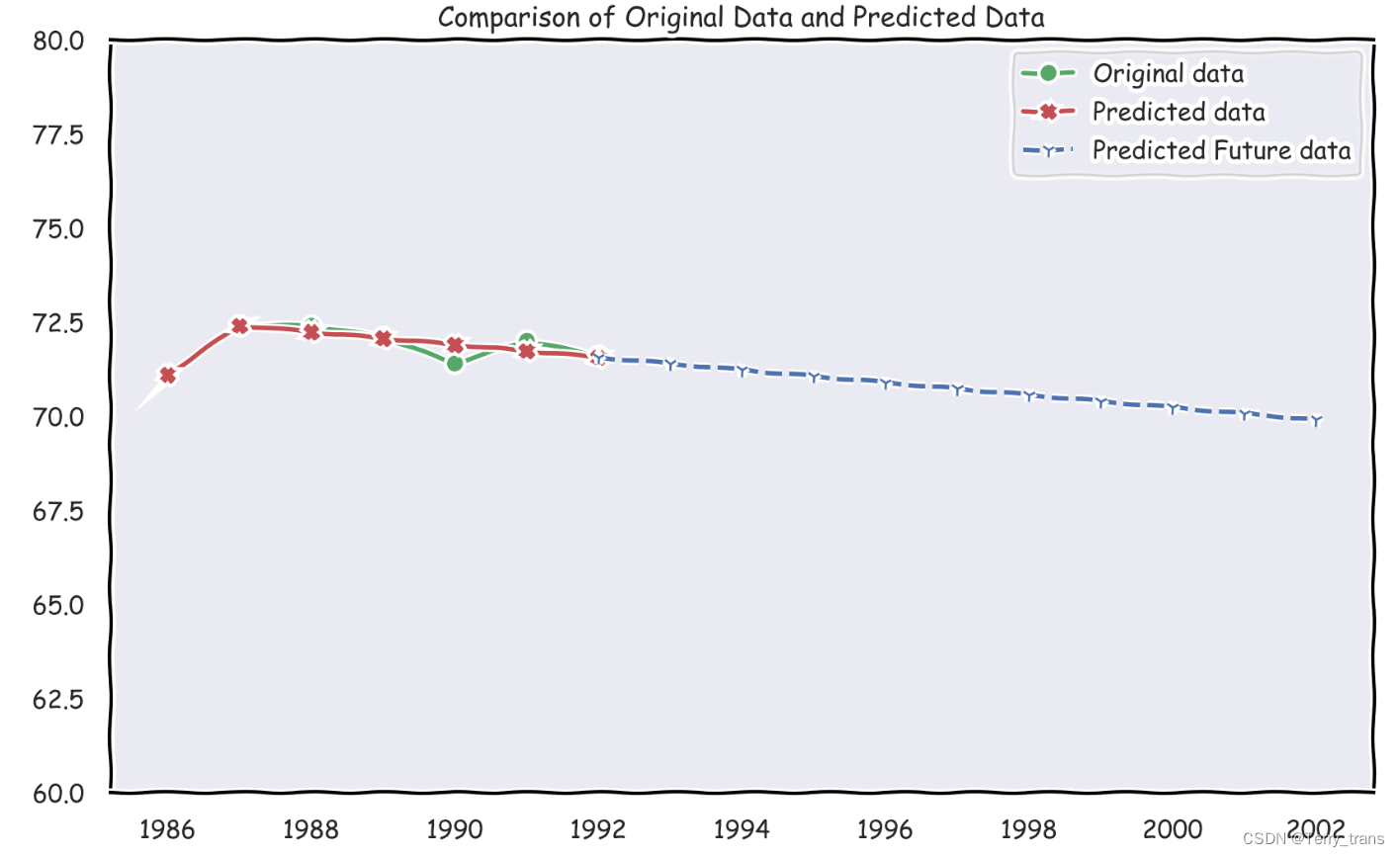





![C++ lambda [],[=] ,[],[this] 的使用](https://img-blog.csdnimg.cn/direct/19b17deddfa24d78a8ec746f65db9511.png)