【算法】{画决策树 + dfs + 递归 + 回溯 + 剪枝} 解决排列、子集问题（C++）

文章目录

1. 前言
2. 算法例题理解思路、代码
- 46.全排列
- 78.子集
3. 算法题练习
- 1863.找出所有子集的异或总和再求和
- 47.全排列II
- 17.电话号码的字母组合

1. 前言

dfs问题 我们已经学过，对于排列、子集类的问题，一般可以想到暴力枚举，但此类问题用暴力解法一般都会超时，时间开销过大。
对于该种问题，重点在于尽可能详细的画决策树，随后根据决策树分析题目所涉及的剪枝、回溯、递归等细节问题。
根据决策树的画法不同，题目会有不同的解法，只要保证决策树没有问题，保证细节问题下代码一定可以编写出来。

2. 算法例题理解思路、代码

46.全排列

思路

思路：求出数组中元素的所有排列顺序，并用数组输出。
解法一：暴力枚举
- 用n层for循环，每层循环依次固定一个数
- 超时，时间开销太大，n个元素就是O(n ^ n)
解法二： 根据决策树进行递归
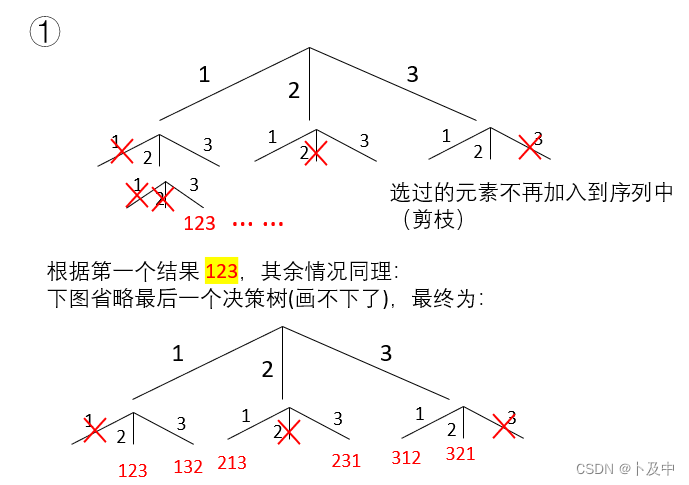
- 根据上图，我们需要创建下面三个全局变量.
- 结束条件：当我们遍历到叶子节点时（即path.size() == nums.size()），将path加入到ret中，并向上返回。
- 回溯：对当前元素dfs后，进行回溯，回溯即将之前加入到path 的元素删除，并将used重新置为false。

代码

class Solution {
public:
    vector<vector<int>> ret; // 用于存储最终结果
    bool used[7]; // 用于记录某个下标的元素是否在序列中
    vector<int> path; // 用于记录某个下标的元素是否已经加入到序列中
    vector<vector<int>> permute(vector<int>& nums) {
        dfs(nums);
        return ret;
    }

    void dfs(vector<int>& nums) {
        if(path.size() == nums.size())
        {
            ret.push_back(path);
            return;
        }

        // 遍历数组，对每一位都进行dfs && 排列
        for(int i = 0; i < nums.size(); ++i)
        {
            if(used[i] == false) // 如果该位置未加入到当前序列中
            {
                path.push_back(nums[i]);
                used[i] = true;
                dfs(nums);
                // dfs向上返回回来 -> 回溯
                path.pop_back();
                used[i] = false;
            }
        }
    }
};

78.子集

题目要求我们将数组的所有子集统计，并以数组形式返回（空集就是空数组）

解法一

解法： 根据选与不选画决策树
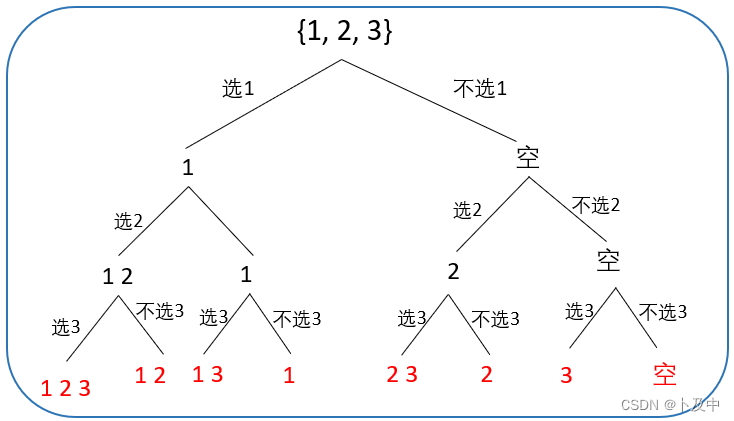
- 根据上图决策树，我们通过对一个元素的选择与否划分树，而当到达叶子节点的时候（i == nums.size()）向上返回即可。
- 函数头：首先需要的参数是数组本身，其次我们通过变量i来标记当前选择的元素所在层数，则 void dfs(vector<int>& nums, int i)
- 函数体：分别写出选择与不选择该元素时的代码即可
- 结束条件：如前面所说，当到叶子节点时返回。

代码

class Solution {
public:
    vector<vector<int>> ret;
    vector<int> path;
    vector<vector<int>> subsets(vector<int>& nums) {
        int i = 0;
        dfs(nums, i);
        return ret;
    }

    void dfs(vector<int>& nums, int i)
    {
        if(i == nums.size())
        {
            ret.push_back(path);
            return;
        }

        // 不选当前元素
        dfs(nums, i + 1);

        // 选当前元素
        path.push_back(nums[i]);
        dfs(nums, i + 1);
        path.pop_back();
    }
};

解法二

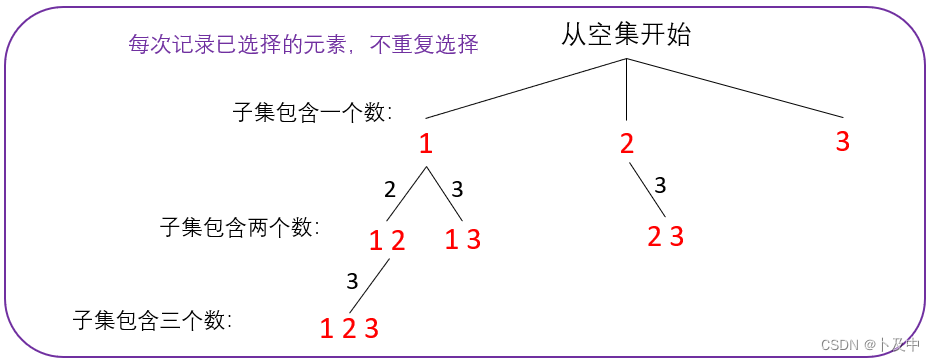
解法： 根据子集包含的元素个数画决策树
如上图所示，以此法画的决策树，每个节点的值都是有效值
- 函数头：第一个参数是数组本身，另外需要给出当前遍历到nums的第几个元素。void dfs(vector<int>& nums, int pos)
- 函数体：
  1. 在函数开始时先将当前子集加入到ret中
  2. 利用for循环，每次从pos开始遍历数组：每次将一个元素作为子集第一位的所有子集检索完毕后，再以下一个元素作为子集第一位，可以防止重复子集
    - for循环中每次将当前元素加入到path中，dfs下一位，最后回溯

代码

class Solution {
public:
    vector<vector<int>> ret;
    vector<int> path;
    vector<vector<int>> subsets(vector<int>& nums) {
        int pos = 0;
        dfs(nums, pos);
        return ret;
    }

    void dfs(vector<int>& nums, int pos)
    {
        ret.push_back(path);
        for(int i = pos; i < nums.size(); ++i)
        {
            path.push_back(nums[i]);
            dfs(nums, i + 1);
            path.pop_back(); // 回溯 - 恢复现场
        }
    }
};

3. 算法题练习

1863.找出所有子集的异或总和再求和

思路

题目分析：题目要求求出数组中所有子集的异或和的总和，我们只需要根据上图求子集的思路，在统计子集时，直接用变量计算异或值即可
- 解法： dfs + 决策树
  - 这道题的决策树与上题一致，只需要在执行方面进行更改。
  - 回溯：由于一个元素异或一个数两次，相当于没有异或，所以对于回溯操作，我们只需要再次进行异或即可。

代码

class Solution {
public:
    int ret = 0; // 最终结果
    int xorSum = 0; // 记录一个子集的异或和
    int subsetXORSum(vector<int>& nums) {
        dfs(nums, 0);
        return ret;
    }

    void dfs(vector<int>& nums, int pos)
    {
        ret += xorSum;

        for(int i = pos; i < nums.size(); ++i)
        {
            xorSum ^= nums[i];
            dfs(nums, i + 1);
            xorSum ^= nums[i]; // 回溯现场 / 异或同一个数两次相当于无异或
        }
    }
};

47.全排列II

思路

题目分析：
根据上图，制定决策树：
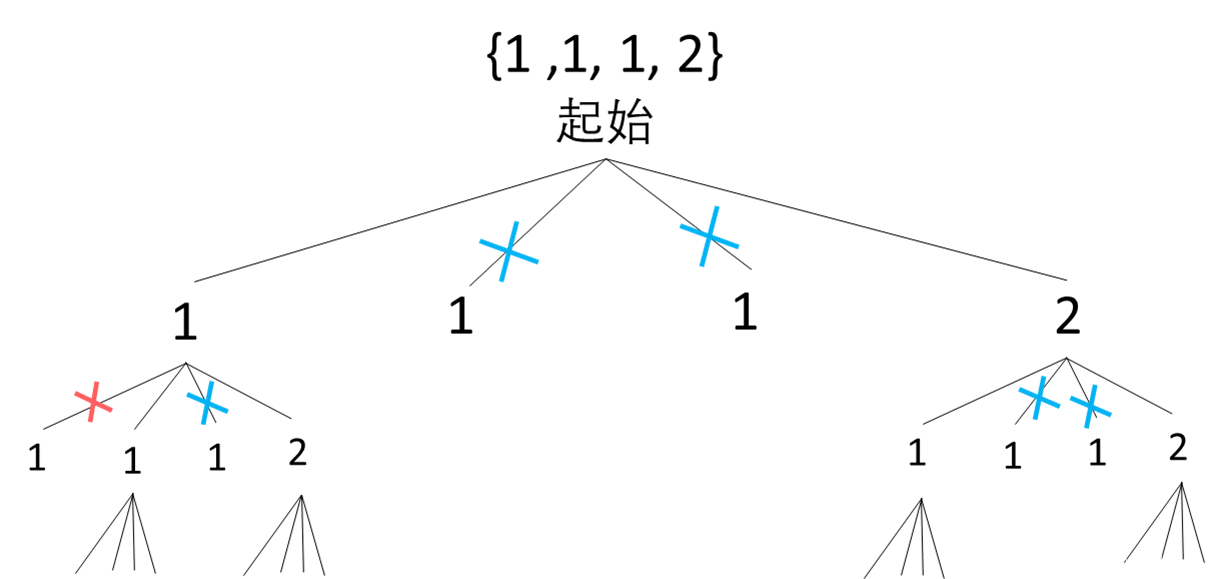
下面是对于上面决策树的解释，以及根据该决策树，我们如何设计代码：
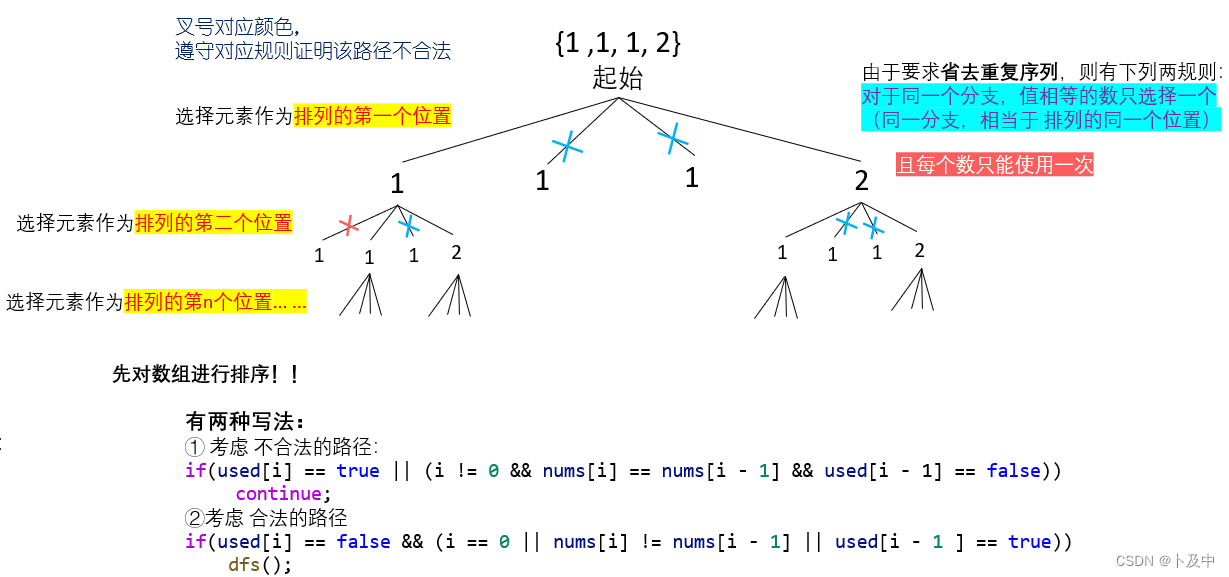
我们对上面探讨的两种解法进行解释：
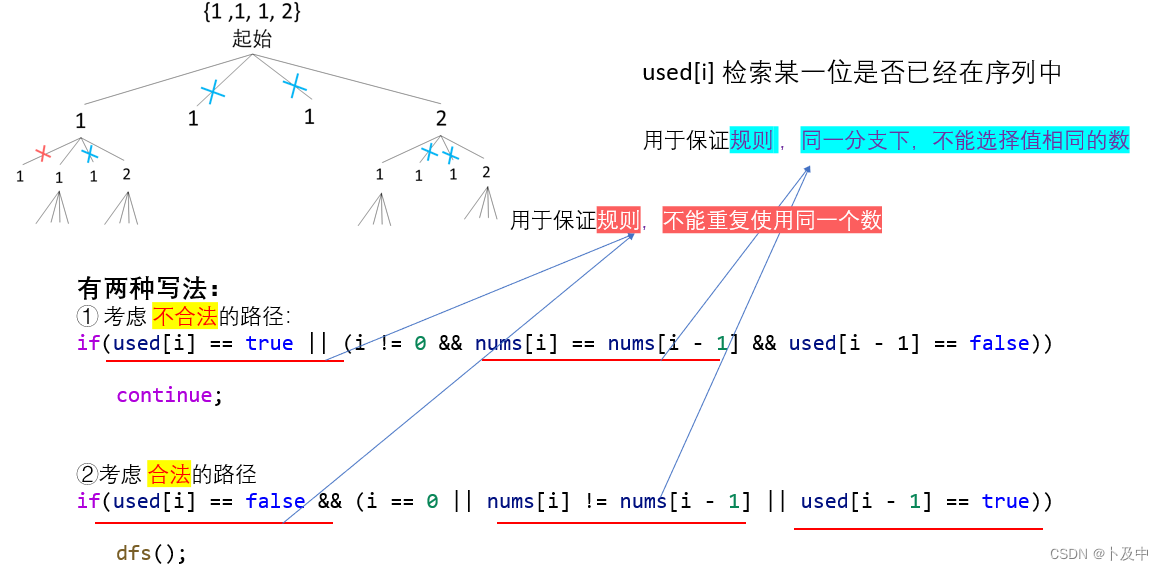
- 如图所示，如果用文字解释，对于不合法路径：
  - 当【当前元素A已经使用了 && 该分支下已有与当前元素值相同的B && B已经在序列中】时不合法。
编写代码方面，本道题与前面的题非常类似，主要在于主逻辑的差别：

代码

class Solution {
public:
    vector<vector<int>> ret;
    vector<int> path;
    bool used[9];

    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end()); // 先排序数组
        dfs(nums, 0);
        return ret;
    }

    void dfs(vector<int> nums, int pos)
    {
        if(path.size() == nums.size())
        {
            ret.push_back(path);
            return;
        }

        for(int i = 0; i < nums.size(); ++i)
        {
            // 剪枝 - 考虑合法路径
            if(used[i] == false && (i == 0 || nums[i] != nums[i - 1] || used[i - 1] == true))
	        {
                path.push_back(nums[i]);
                used[i] = true;
                dfs(nums, pos + 1);
                path.pop_back();
                used[i] =  false;
            }
        }
    }
};

17.电话号码的字母组合

思路

解法： dfs + 决策树
- 决策树：如下图所示

本体决策树画出来后，递归回溯等部分相对于前面简单一些
- 细节问题：
  - 我们需要由数字与字符串一一对应来进行号码的模拟，这里可以用哈希表 ——> 优化：数组作为哈希表hash
  - 主逻辑：关于for循环，我们需要从digits中依次提取数字字符，并找到相对应的字符串，即hash[digits[pos] - '0']

代码

class Solution {
public:
    // 数组作哈希，下标对应字符串
    string hash[10] = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
    string path;
    vector<string> ret;
    vector<string> letterCombinations(string digits) {
        // 特殊情况
        if(digits.size() == 0) return ret;

        dfs(digits, 0);
        return ret;
    }

    void dfs(string& digits, int pos) {
        if(path.size() == digits.size())
        {
            ret.push_back(path);
            return;
        }

        for(char ch : hash[digits[pos] - '0']) // 提取数字字符
        {
            path.push_back(ch);
            dfs(digits, pos + 1);
            path.pop_back();
        }
    }
};