引言
在机器学习领域,回归模型是一种预测连续数值输出的重要工具。无论是预测房价、股票价格还是天气温度,回归模型都扮演着不可或缺的角色。然而,构建模型只是第一步,评估模型的性能是确保模型准确性和泛化能力的关键环节。本文将详细介绍几种常用的回归模型评估方法。
一、 均方误差(Mean Squared Error, MSE)
均方误差是最常用的回归评估指标之一,它计算了预测值与真实值之间差异的平方的平均值。公式如下:
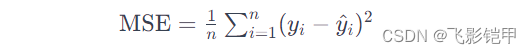
其中,yi 是第 i 个观察到的真实值,y^i 是第 i 个预测值,n 是样本数量。MSE 的值越小,表示模型的预测能力越强。
二、均方根误差(Root Mean Squared Error, RMSE)
均方根误差是均方误差的平方根,提供了与原始数据相同单位的误差大小评估。其公式为:

RMSE 对于较大的误差会给予更大的惩罚,因此它在某种程度上能更好地反映模型预测的准确性。
三、平均绝对误差(Mean Absolute Error, MAE)
平均绝对误差是另一种衡量预测值与真实值之间差异的方法,它计算了这些差异绝对值的平均数。其公式为:

MAE 相比 MSE 和 RMSE,对异常值的敏感度较低,因此在存在异常值的数据集上可能是更好的选择。
四、R²(决定系数)
R²,也称为决定系数,是衡量模型解释变量变异性的一种指标。它表示模型预测值与真实值之间的相关程度。R² 的值范围从 0 到 1,接近 1 表示模型能够很好地解释目标变量的变异性。其公式为:

其中,yˉ 是真实值的平均值。R² 越高,表明模型的拟合度越好。
五、调整 R²
调整 R² 是对 R² 的改进,考虑了模型中自变量的数量。它解决了传统 R² 随着模型中变量数量增加而自动增加的问题,提供了一个更加公正的评估指标。其公式为:
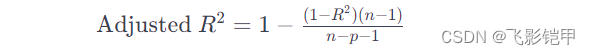
其中,(n) 是样本数量,(p) 是模型中预测变量的数量。调整 R² 更适合于比较包含不同数量自变量的模型。
结语
回归模型的评估是一个复杂但至关重要的过程。通过理解和应用上述几种评估方法,我们可以更准确地衡量模型的性能,从而构建出更加强大和准确的预测模型。在实践中,选择哪种评估方法取决于具体任务的需求以及数据的特性,有时甚至需要结合使用多种方法来获得最全面的评估。