快乐数原题地址
方法一:哈希集合
定义函数 getNext(n) ,返回 n 的所有位的平方和。一直执行 n=getNext(n) ,最终只有 2 种可能:
- n 停留在 1 。
- 无限循环且不为 1 。
证明:情况 1 是存在的,如力扣的示例一:

接下来只需证明,反复执行 getNext 操作,最终一定会无限循环(停留在 1 可以理解为无限的 1→1 循环)。
分类讨论:
- n 的位数 ≤3 ,那么 getNext(n)<=getNext(999)=243 ,那么反复执行 getNext(n) ,执行 244 次以上,根据抽屉原理,一定会出现循环。
- n 的位数 >3 ,如 n 为 4 位数,执行 getNext(n) 后, n 的位数会减小,直到变为情况 1 。
所以,我们可以使用如下算法:反复执行 n=getNext(n) ,会出现下面 3 种情况:
- n=1 ,说明原来的 n 是快乐数。
- n 不在哈希表中,则把 n 插入哈希表。
- n 在哈希表中,且 n≠1 ,说明 n 已经进入循环,原来的 n 不是快乐数。
// 方法一:哈希集合
class Solution
{
public:
bool isHappy(int n)
{
unordered_set<int> hashtable;
while (n != 1)
{
// 若哈希表中没有 n ,就添加 n ,否则不是快乐数
if (!hashtable.count(n))
{
hashtable.insert(n);
}
else
{
return false;
}
n = getNext(n);
}
return true;
}
private:
// 计算 n 的所有位的平方和
int getNext(int n)
{
int sum = 0;
while (n)
{
int digit = n % 10;
n /= 10;
sum += (digit * digit);
}
return sum;
}
};方法二:快慢指针(龟兔赛跑、弗洛伊德循环查找算法)
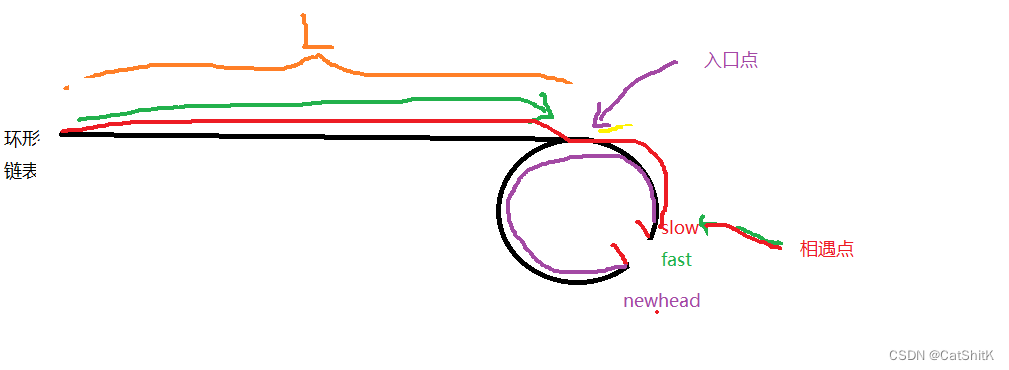
考虑到反复执行 n=getNext(n) ,一定会进入循环,参考判断链表是否带环的思路,定义 fast 和 slow , slow 每次执行 slow=getNext(slow) 一次, fast 每次执行 fast=getNext(fast) 两次,那么 slow 和 fast 最终一定会在循环内相遇。若相遇时 slow=fast=1 ,则 n 为快乐数,否则不是快乐数。
这是因为若链表带环,最终 fast 和 slow 一定会入环,且每次 fast 比 slow 多走一步, fast 和 slow 的距离缩短一步,最终距离一定会减为 0 ,两者相遇。
// 方法二:快慢指针法
class Solution
{
public:
bool isHappy(int n)
{
int slow = n;
int fast = getNext(slow);
while (slow != fast)
{
// 慢指针一次走一步
slow = getNext(slow);
// 快指针一次走两步
fast = getNext(getNext(fast));
}
return slow == 1;
}
private:
// 计算 n 的所有位的平方和
int getNext(int n)
{
int sum = 0;
while (n)
{
int digit = n % 10;
n /= 10;
sum += (digit * digit);
}
return sum;
}
};方法三:数学
根据方法一所述,反复执行 n=getNext(n) , n 一定会跌为三位数以下,且进入循环。使用硬编码穷举,最终的循环一定是 ...,4,16,37,58,89,145,42,20,4,... 或者 ...,1,1,...
所以只需要提前把循环中的数存储在哈希表中,反复执行 n=getNext(n) ,会出现 3 种情况:
- n 在哈希表中,说明已经进入循环,原来的 n 不是快乐数。
- n=1 ,说明原来的 n 是快乐数。
- n 不在哈希表中。
// 方法三:数学
class Solution
{
public:
bool isHappy(int n)
{
while (1)
{
// 最终要么为 1 ,要么进入循环
if (n == 1)
{
return true;
}
else if (cycleMembers.count(n))
{
return false;
}
n = getNext(n);
}
}
private:
// 计算 n 的所有位的平方和
int getNext(int n)
{
int sum = 0;
while (n)
{
int digit = n % 10;
n /= 10;
sum += (digit * digit);
}
return sum;
}
static unordered_set<int> cycleMembers;
};
unordered_set<int> Solution::cycleMembers = { 4,16,37,58,89,145,42,20 };