1.前言 

前五题在这http://t.csdnimg.cn/UeggB

后三题在这http://t.csdnimg.cn/gbohQ

给定一个链表，判断链表中是否有环。http://t.csdnimg.cn/Rcdyc 

记录每天的刷题，继续坚持！

2.OJ题目训练

10. 给定一个链表，返回链表开始入环的第一个结点。 如果链表无环，则返回 NULL

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

本题是上一题（链接在上）的延续，不清楚的小码喵可以去上一篇博客观看一下。

方法一

思路

为了方便分析，我们把示例图简化一下涉及一点数学思维，大家做好准备。

我们依然按照上题来定义两个快慢指针，fast一次前进两步，slow一步

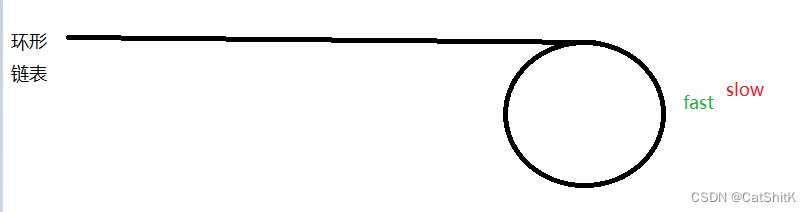
如果为环，那么fast和slow终会在环中相遇，这里假设已经相遇了。

注意以下的单位为节点数

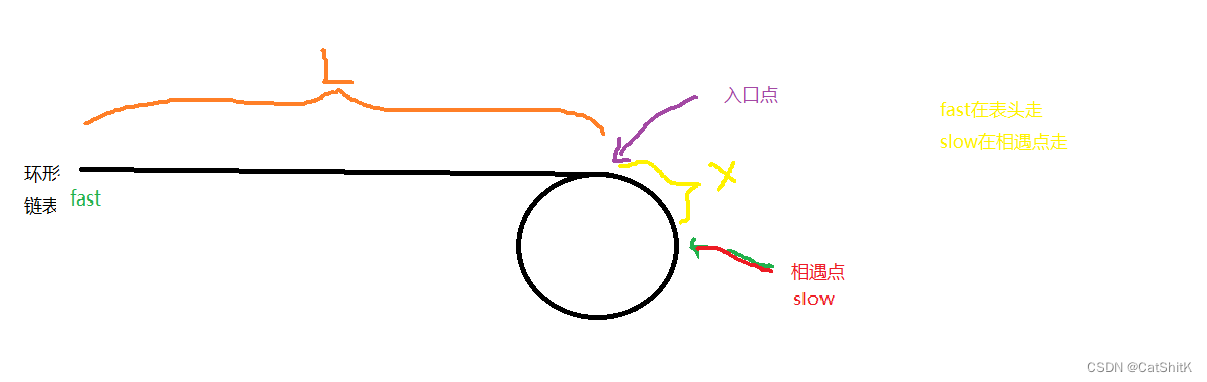
入口点：链表开始入环的第一个节点

相遇点：fast和slow相遇的节点

假设起点到入口点长度:L
假设环的周长是:C
假设入口点到相遇点的长度是:X

由于fast走过的距离是链表起点>>入口点 + 在环中移动的圈数（必须转圈才能做到跟slow相遇）+ 入口点到相遇点的距离

slow是链表起点>>入口点 + 入口点到相遇点的距离

fast走的距离是slow的两倍，那么我们可以得出：

fast移动的距离：L+C+X

slow移动的距离：L+X

两倍关系：L+C+X=2(L+X)

但是上面fast公式的C我们要画上一个问号，因为fast可能在环中不止会转一圈，可能会转很多圈（环足够小），所以我们再改进公式得到：

fast移动的距离：L+n*C+X         n为fast在环中循环的圈数

slow移动的距离：L+X

两倍关系：L+n*C+X=2(L+X)

                ↓

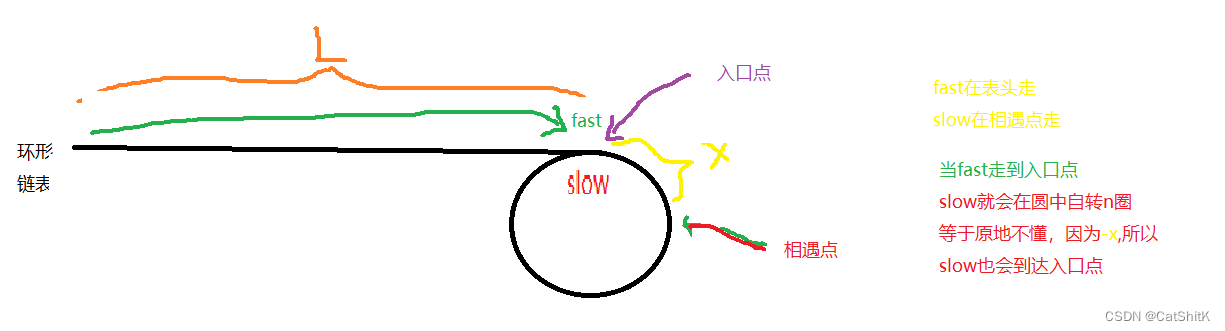
        L = n*C - X

得出关系：链表头走到起点的距离 = n倍的周长再减去相遇点到起点的距离

进而得出：一个指针从表头走，一个指针从相遇点走，那么他们会在入口点相遇!

附源代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode *fast;
    struct ListNode *slow;
    fast = slow = head;
    while(fast&&fast->next&&slow->next)
    {
        fast=fast->next->next;
        slow=slow->next;
        if(fast == slow)    //相遇
        {
            struct ListNode *tou = fast;    //相遇点,相遇时再创建节约空间
            while(head!=tou)    //向下继续走，直到他们相遇就是起点
            {
                head = head ->next;
                tou = tou -> next;
            }
            return tou; 
        }
        
    }

    return NULL;    //无法相遇则不为环形链表
}

方法二

本题还有一个极为简单的解法，但是相对繁琐，我们要用到之前刷过的一题。（CV一下）

这里给大家一个链接看看大家能不能自己想出方法：160. 相交链表 - 力扣（LeetCode）

思路

我们可以利用更新奇的办法：分割链表，来把一个链表变为两个，再利用相交链表的方法来求出他们的起点。

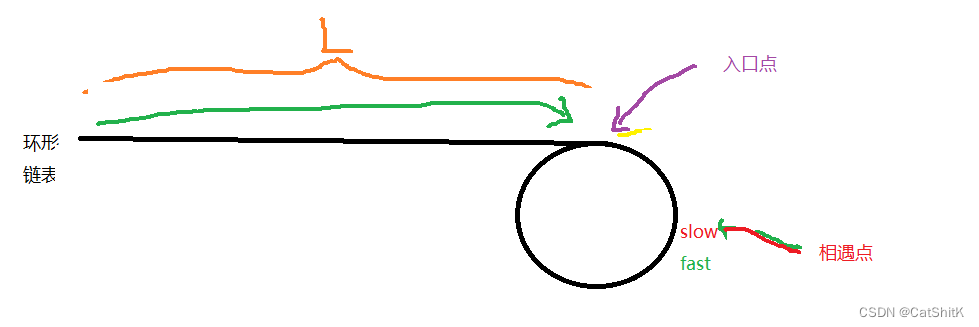
当fast和slow相遇时，我们记录这个相遇点

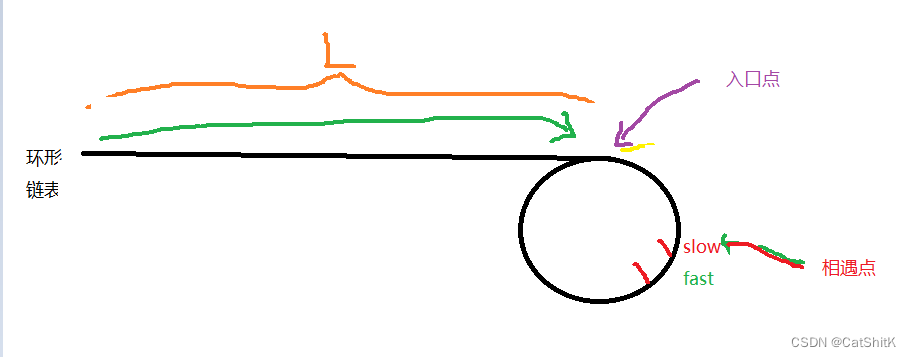
之后再记录下一个点，我们就可以把相遇点断开，称为newhead

这样，环形链表，和newhead组成的表，就可以运用相交链表的方法，达到入口点既交点的节点了

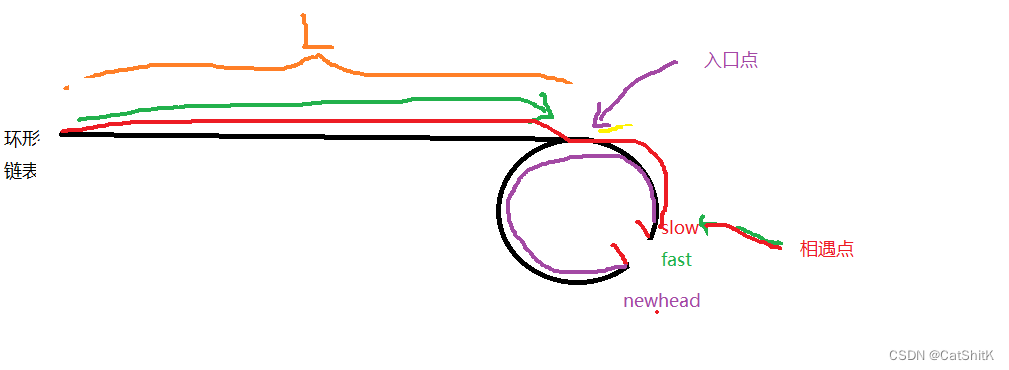
如图，红色和紫色，既两个相交链表

注意事项

• 相交链表那块要足够清楚，我们是将问题牵线搭桥到那里去的，所以要足够理解
• 直接CV

附源代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */

//返回相交链表相交节点的函数

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    struct ListNode *curA=headA;
    struct ListNode *curB=headB;
    int lenA=1,lenB=1;  //链表的长度至少为1
    while(curA->next)   //计算链表A的长度及尾节点
    {
        lenA++; //顺便计算表长
        curA=curA->next;
    }
    while(curB->next)
    {
        lenB++;
        curB=curB->next;
    }
    if(curA!=curB)
    {
        return NULL;    //两边的为节点不相同，那根本不是相交链表
    }

    int gap=abs(lenA-lenB); //abs为取绝对值
    struct ListNode *longlist=headA;    //假设A为长节点，这里我们利用替身来表示长表
    struct ListNode *shortlist=headB;   //就可以节省很多判断语句
    if(lenB>lenA)                       //若B长，侧替换
    {
        longlist=headB;
        shortlist=headA;
    }
    while(gap--)
    {
        longlist=longlist->next;    //先走差值步
    }
    while(longlist!=shortlist)  //不等于则同时向前遍历，直到相等
    {
        longlist=longlist->next;
        shortlist=shortlist->next;
    }
    return longlist;    //返回第一个相等值
}

//此题函数
struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode *fast;
    struct ListNode *slow;
    fast = slow = head;
    while(fast&&fast->next&&slow->next)
    {
        fast=fast->next->next;
        slow=slow->next;
        if(fast == slow)    //相遇
        {
            struct ListNode *tou = fast;    //相遇点,相遇时再创建节约空间
            struct ListNode *newhead = tou->next; //新表头为相遇的下一个节点
            tou->next = NULL;   //将相遇点断开
            return getIntersectionNode(newhead, head);
        }
    }
    return NULL;    //无法相遇则不为环形链表
}