A. A+B?

给出长度为3的字符串,计算字符串表示的表达式的值。
思路:。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 2e5 + 5;
int t;
std::string s;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> t;
while(t --) {
std::cin >> s;
std::cout << s[0] - '0' + (s[2] - '0') << '\n';
}
return 0;
}B. Matrix Rotation

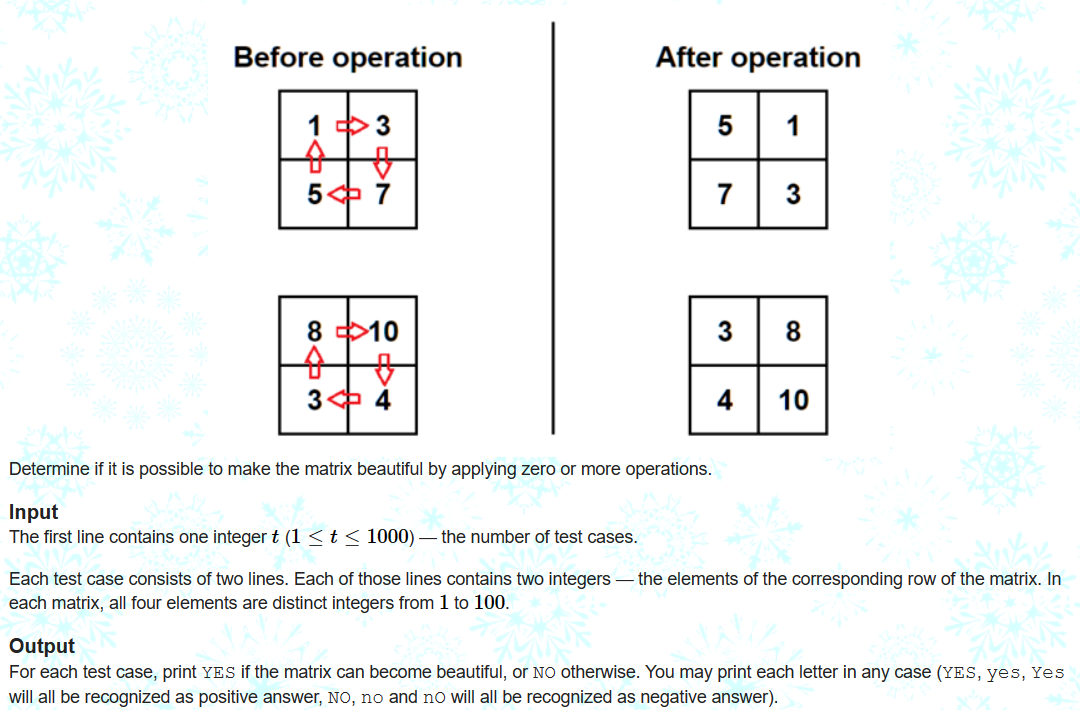
给出2*2的矩阵,每次可以将其旋转变化,问是否能通过旋转变化使得满足每一行每一列第一个数小于第二个数。
思路:保存旋转后的数组,挨个判断即可。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 2e5 + 5;
int t;
int a[5][5], b[5][5], c[5][5], d[5][5];
bool check(int a[5][5]) {
if(a[1][1] < a[1][2] &&a[2][1] < a[2][2] && a[1][1] < a[2][1] && a[1][2] < a[2][2])
return true;
else
return false;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> t;
while(t --) {
for(int i = 1; i <= 2; i ++) {
for(int j = 1; j <= 2; j ++) {
std::cin >> a[i][j];
}
}
b[1][1] = a[2][1], b[1][2] = a[1][1],
b[2][1] = a[2][2], b[2][2] = a[1][2];
c[1][1] = b[2][1], c[1][2] = b[1][1],
c[2][1] = b[2][2], c[2][2] = b[1][2];
d[1][1] = c[2][1], d[1][2] = c[1][1],
d[2][1] = c[2][2], d[2][2] = c[1][2];
if(check(a) || check(b) || check(c) || check(d))
std::cout << "YES" << '\n';
else
std::cout << "NO" << '\n';
}
return 0;
}os:学习了一波函数中二维数组的引用,,乐了,之前从来没用过
C. Different Differences

定义一个递增数组的characteristic为该数组相邻两数之差不同数字的个数。给出最大值和需要组成数组的长度,构造一个characteristic最大的递增数组。
思路:最大值很小,直接列举差递增的数字,然后遍历查找最大的满足条件的即可。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 2e5 + 5;
int t, n, k;
int a[] = {0, 1, 2, 4, 7, 11, 16, 22, 29, 37, 46};
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> t;
while(t --) {
std::cin >> k >> n;
std::vector<int> vec;
int pos;
for(int i = 9; i >= 1; i --) {
if(a[i] <= n && i + n - a[i] >= k) {
pos = i;
break;
}
}
pos = std::min(k, pos);
for(int i = 1; i <= pos; i ++) {
vec.push_back(a[i]);
}
int cnt = k - pos;
for(int i = a[pos] + 1; i <= a[pos] + cnt; i ++) {
vec.push_back(i);
}
for(auto u : vec)
std::cout << u << ' ';
std::cout << '\n';
}
return 0;
}D. Absolute Sorting

给出数组,是否存在一个数,使得数组中所有数变为与该数差的绝对值后,数组为非递减序列。
思路:比较简单的思路可以这样想,每相邻两个数比较都可以给这个数提供一个范围,取所有范围的交集即可。分情况讨论,当a[i] > a[i - 1]时,左边界x为-INF,右边界为(a[i] + a[i - 1]) / 2;当a[i] < a[i - 1]时,右边界为INF,左边界为(a[i] + a[i - 1] + 1) / 2,对于每次得出的范围,用l和r取一下极值即可,注意l和r一开始是[-INF, INF]。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
#define INF 0x3f3f3f3f
const int N = 2e5 + 5;
int t, n;
int a[N];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> t;
while(t --) {
std::cin >> n;
for(int i = 1; i <= n; i ++) {
std::cin >> a[i];
}
int l = 0, r = INF;
for(int i = 2; i <= n; i ++) {
int x = 0, y = INF;
if(a[i] > a[i - 1])
y = (a[i] + a[i - 1]) / 2;
else if(a[i] < a[i - 1])
x = (a[i] + a[i - 1] + 1) / 2;
l = std::max(l, x);
r = std::min(r, y);
}
if(l > r)
std::cout << -1 << '\n';
else
std::cout << l << '\n';
}
return 0;
}E. Permutation Game

给出一个长度为n的排列,初始情况每个数都是红色,先手先进行操作,每次操作可以选择一项进行:(1)将一个数染成蓝色;(2)选择一些蓝色的数将其重新排序;(3)什么也不做。若排列按照升序排列,则先手胜,若按照降序排列,则后手胜,否则平局,给出序列,判断胜负情况。
思路:学习大佬令cnt1记录的是a[i] = i的个数,即先手不需要染色的部分,cnt2记录的是a[i] = n - i + 1的个数,即后手不需要染色的部分;cnt记录的是不满足前面两种情况的个数,即两人都需要染色的部分。对于先手需要染色的cnt2 + cnt部分,根据策略,先手必定先染色cnt2部分;后手则会先染色cnt1部分。根据这个我们可以直接判断:若cnt2 + cnt <= cnt1,则先手一定先比后手染色完,先手胜;若cnt1 + cnt < cnt2,则后手比先手先染色完成,后手胜,没有等号是因为先后手原因;其他情况则是平局。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 5e5 + 5;
int t, n;
int a[N];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> t;
while(t --) {
std::cin >> n;
for(int i = 1; i <= n; i ++) {
std::cin >> a[i];
}
int cnt1 = 0, cnt2 = 0, cnt = 0;
for(int i = 1; i <= n; i ++) {
if(a[i] == i)
cnt1 ++;
else if(a[i] == n - i + 1)
cnt2 ++;
else
cnt ++;
}
if(cnt2 + cnt <= cnt1)
std::cout << "First" << '\n';
else if(cnt1 + cnt < cnt2)
std::cout << "Second" << '\n';
else
std::cout << "Tie" << '\n';
}
return 0;
}
os:妙啊!
F. Copy of a Copy of a Copy


给出一个n*m的01矩阵,每次可以进行如下操作:选择一个位置,该位置四个方向的01情况与该位置不同,将该位置01变换,创建改变后的拷贝矩阵。现在给出k个拷贝矩阵和原矩阵,但是顺序并不是按照操作顺序的,现在需要找出初始矩阵,并输出操作方案。
思路:对于k个矩阵,我们需要找出满足条件可以修改的位置个数,按照这个个数排序,我们就可以得到k+1个矩阵的原始顺序。相邻两个矩阵比较,哪个位置不同,则是修改了哪个位置。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
typedef std::pair<int, int> PII;
const int N = 35;
int t, n, m, k;
struct node {
char mp[N][N];
int id, cnt;
} e[105];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> n >> m >> k;
k ++;
for (int l = 1; l <= k; l ++) {
e[l].id = l;
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= m; j ++) {
std::cin >> e[l].mp[i][j];
}
}
for (int i = 2; i < n; i ++) {
for (int j = 2; j < m; j ++) {
if (e[l].mp[i][j] != e[l].mp[i - 1][j] && e[l].mp[i][j] != e[l].mp[i + 1][j]
&& e[l].mp[i][j] != e[l].mp[i][j + 1] && e[l].mp[i][j] != e[l].mp[i][j - 1])
e[l].cnt ++;
}
}
}
std::sort(e + 1, e + 1 + k, [](node & a, node & b) {
return a.cnt > b.cnt;
});
std::vector<PII> ans;
for (int l = 2; l <= k; l ++) {
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= m; j ++) {
if (e[l].mp[i][j] != e[l - 1].mp[i][j])
ans.push_back({i, j});
}
}
ans.push_back({-1, e[l].id});
}
std::cout << e[1].id << '\n';
std::cout << ans.size() << '\n';
for (auto u : ans) {
if (u.first == -1)
std::cout << 2 << ' ' << u.second << '\n';
else
std::cout << 1 << ' ' << u.first << ' ' << u.second << '\n';
}
return 0;
}