书籍信息

书名：《我是个怪圈》
作者：(美)侯世达
资源：https://download.csdn.net/download/zhiyuan411/87367224，密码：book

论灵魂及其尺寸

一只羔羊是否也拥有不容轻视的灵魂呢？
一条鳟鱼咬上了钩，它有逃过此劫而幸存下来的理由吗？
蟋蟀、蚊子乃及细菌是否也拥有微弱的内在“亮光”？
用力咀嚼的是哪一个西红柿？
应该砍倒前院那株枝繁叶茂的榆树吗？
拔掉疯长的那些野草呢？

那一条定命而致命的线，该画在何处？

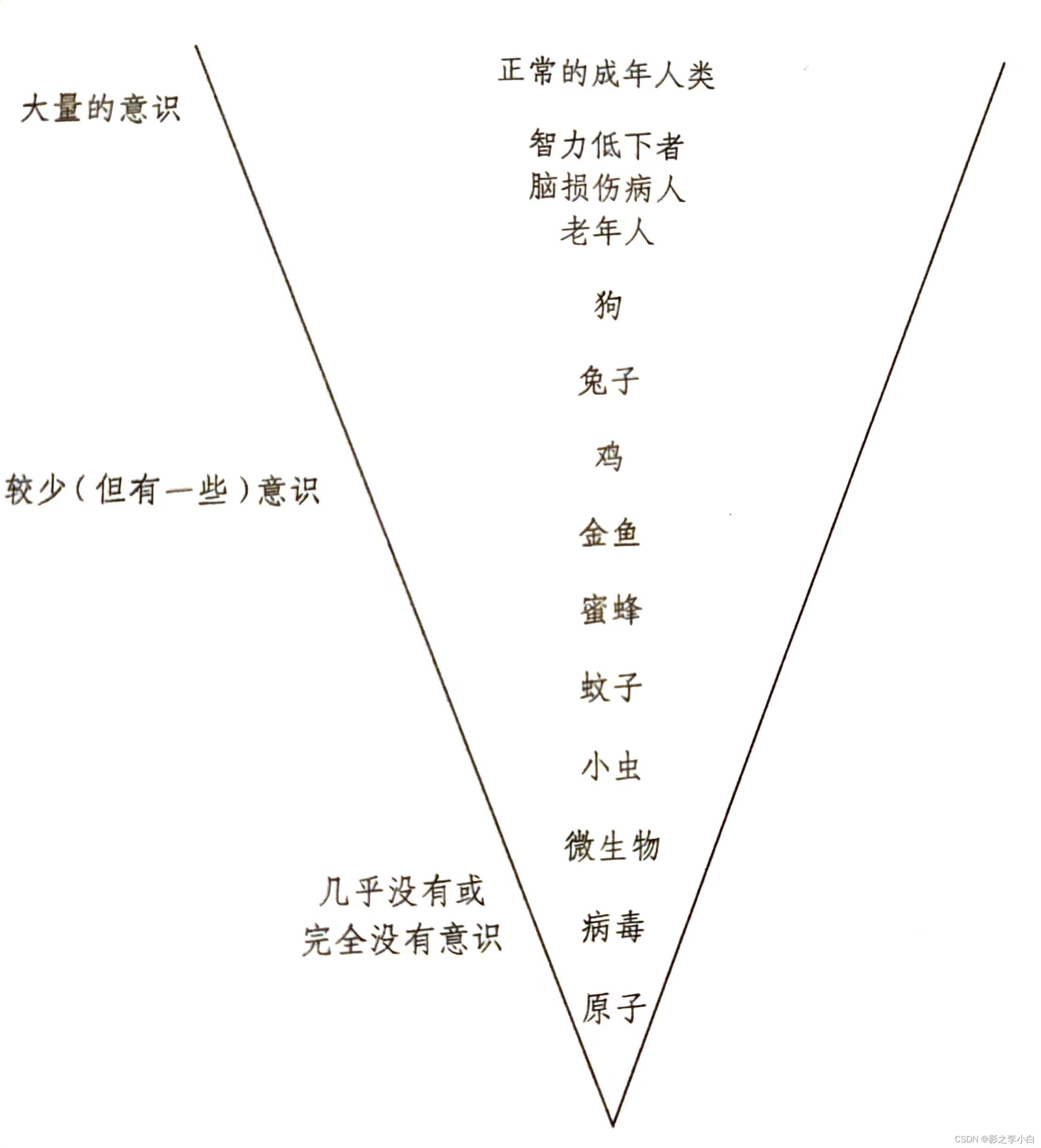
所谓“灵魂”或“我”之物，也可以说成是“内在有光”、“拥有内在性”或者作为万年备胎的“有意识”，差别都不大。所有这些术语都必须被理解为滑动在一个标尺上的“程度”，而不是或开或关、非黑即白、是非分明的开关。

摇曳在恐惧与梦想之间的那只电灯泡（取自拉塞尔·埃德森的诗）

热力学可由统计力学来解释。在热力学层面进行讨论时，统计力学可以被绕过不提。

思考力学可由统计思维学来解释。在思考力学层面进行讨论时，统计思维学可以被绕过不提。

思考力学，专注于脑中大规模的结构与模式：人们如何做出决策、如何犯下错误、如何感知到模式、如何体验新奇的提醒，诸如此类。

“思维学”指的是小规模的现象：神经递质如何在突触之间传播、细胞如何连接在一起、细胞集群如何共振，诸如此类。“统计思维学”指那些非常小的实体经过平均化以后的集体行为。

模式的因果潜力

多米诺链阵：

规定每张多米诺牌中都以一种巧妙的方式装载着弹簧（我们不关心具体的细节），经过一段“顽固”期后，它会弹回原来的竖直状态。
我们可以用这样一种系统实现一种机械计算机，把信号沿着多米诺骨牌传递下去，那些牌可以分叉，也可以交汇；如此一来，信号既可以在环路中扩增，也可以联合引发其他的信号，执行诸如此类的行为。
这是一个经过了精确时间调配的多米诺骨牌链阵网络，而其相当于执行某种特定运算的计算机程序，比如判断一个输入的数字是否为质数。

设想在多米诺链阵中输入641这个数字之时，一位观察者正站在旁边。这位观察者事先并不知道排出这个链阵的意图何在，于是在用心观察一段时间之后，他指着因数分支中的一张多米诺骨牌充满好奇地发问：“为什么那里的那张多米诺骨牌从来都不倒呢？”

第一种答复：“因为它前面那张牌从来不倒”。采取了一种微观的视角。
第二种答复：“因为641是一个质数”。没有提及任何具有物理性质的东西，聚焦点向上移动到了链阵的集体属性之上，而且那些属性以某种方式超越了物理层面，而与纯粹的抽象概念相关。

虽然在较低层级上发生之事是造成在较高层级上发生之事的根由，但是却仍然与较高层级不相关。
更高的层级可以无牵无挂地忽视更低层级上的过程。

闹壳：

想象一个没有摩擦力的台球桌（称为“闹壳”），桌面上有不止16个台球，还摆放着数不清的极小的弹子，我们将它们命名为“小交弹”（“交互作用的小弹子”的缩写）。
在一个绝对扁平的世界中，这些小交弹彼此相互碰撞，还在四壁间来回反弹，永无停歇。
这些小交弹还是具有磁性的（所以让我们把它们的名字改成“小磁交弹”）。当它们以较低的速率撞到彼此时，它们可以黏在一起，形成聚团；将其命名为“小磁交弹球”。
一个小磁交弹球由数目巨大的小磁交弹构成，并且在边缘处频繁地损失一些小磁交弹，同时收获另外的一些。
这个系统里存在着两种极端不同的居民种类：微小、轻盈、飞速移动的小磁交弹，和庞大、沉重、近乎不动的小磁交弹球。

大的小磁交弹球仅仅是一种副现象（epiphenomena）。意思就是说，虽然不可否认它们在那里，但它们对于理解那个系统却并非关键，因为它们是由小磁交弹组成的。

毕竟，我们本身也是相当巨大的副现象，这个事实已经判定我们必须通过与我们的尺寸差不多级别的其他副现象（例如，我们的父母，我们的猫、车和蛋糕，我们的帆船、萨克斯管和檫树）来谈论世界。

站在较高层级的视角上看待闹壳：那些聚团拥有属于自己的生命，它们在桌面上来来回回地移动，彼此交互作用，仿佛桌面上除了它们之外没有任何其他的东西，我们已经不再能看到那些小磁交弹了。

关于自我与符号

拍摄自身画面的电视系统总是欠缺一个关键的方面：与单纯的接收或图像接收相对的感知的能力。
感知的起点是某种由大量微信号组成的输入（可能是二维的图像，但并不一定如此），但是它随后会更进一步，最终在庞大的休眠符号集合中选择性地触发一个小的子集。
符号，即拥有表征品质的离散结构。也就是说，大脑内的一个符号，就像那个假设性的闹壳里的小磁交弹球一样，应该被视作一个可触发的物理结构，并构成了大脑执行一种特定范畴或概念的方式。

进化在人类这一点上裂开了一道惊人的鸿沟，而又渐渐地与其他灵长类动物越隔越远：它们的范畴系统变得可以任意扩展，其在根本上是一种没有限制的可扩展性，与其他物种十分常见的有限性形成了鲜明的对比。

情景记忆是我们私人的情景仓库，而这些情景都曾发生在我们自己、我们的朋友、我们看过的小说、电影、新闻故事或者电视新闻片段中人物的身上，形成了长时记忆的一个主要部分，并令我们如此具有人情味。
显而易见，关于情景的记忆可以被我们目睹的外部事件或者其他已被触发的情景所触发，而且同样显而易见的是，几乎所有关于特别情景的记忆在绝大多数的时间里都处于休眠状态（不然的话，我们会彻底疯掉）。
我们人类与其他的动物不一样，拥有所有这些种类的记忆。

副现象

副现象的玻璃球：

有一天，我想把装在书房地板上那个小纸箱里的信封都拽出来，叠成一组塞到我书桌的一个抽屉里。
于是，我打开了纸箱，把手伸进去，用右手扣住里面那叠信封（大约有100封），然后用力紧压，好把它们一鼓作气地全部拽出箱子。
但是突然之间，我在拇指和其他手指之间感受到了一样让我惊奇的东西。在那只摇摇欲坠的小小硬纸箱的正中心，竟然坐着（或浮着）一颗玻璃球！
我把所有的信封都从盒子里拿了出来，然后试图把它从信封间抖落出来，空空如也。
最终，我还是意识到，这里面本来就没有什么玻璃球，只有某种在感觉里同玻璃球一模一样的东西。它是一种副现象；而引发它的事实是，每个信封在其折叠出“V”字形的顶点处，都叠着三层纸和一层薄薄的胶。当你挤压100张对齐叠在一起的信封时，你不能像挤压其他部位一样压紧那片小小的区域，它能抗压，手感就像玻璃球。

关于闹壳，这个系统可以在两个相距甚远的层级上分别被观察到，两种视角都是合理有效的。

1. 从更高层级的“思考动力学”视角出发，这里发生的是一种符号化的活动，小磁交弹球彼此之间交互作用，而它们所利用的“热能”则来自那些肉眼不可见的小磁交弹的翻滚蒸腾。（可能看起来更加基础，不遗漏任何细节）
2. 从更低层级的“思维统计学”视角出发，则有且只有小磁交弹是真正存在之物，它们的交互作用是以基础性的彼此冲撞和击打的动态完成的。（丢掉了大量信息，完成了高度浓缩的简化，因为它更有效率，所以看起来可能对于我们这些凡人而言也更加有用）

模式与可证性

PM：在《数学原理》（作者：罗素和怀特海）中用于推理集合的形式系统（formal system of Principia Mathematica）。PM是一套精准的符号操作法则。

哥德尔的典型怪圈

奇迹般步调划一的同步

哥德尔想象出了一套自然数，它们像斐波那契的F数一样，经由数字运算，从彼此之间有机地生长出来，但同时也能与PM定理的集合形成一对一的精准映射。

如果你使用排印式的规则R5，从定理X和Y中推导出定理Z，与此同时，如果你运用计算的法则，利用数字x和y算出数字z，那么二者之间就是完全匹配的。
也就是说，如果x是对应定理X的数字而y是对应定理Y的数字，那么z就会“奇迹般地”也成为与定理Z对应的数字。

在公式与大整数之间翻转

一串PM符号（不论其所言是真还是假，甚或只是一堆随机凑在一处的符号团）如何能够系统地转化为一个正整数，反过来，这样一个正整数又如何能够“解码”还原出它所由来的那一串符号。

哥德尔为PM符号中的每一个都指派了一个不同的小整数。遇到多重符号的公式时，就要从左到右，把符号一个一个地替换成它们的编码数字，然后再把所有那些单个的编码数字组合在一起（方法是把它们按顺序作为连续质数的指数，进行乘方运算），形成一个独一无二的大整数。

设（任意）指派给符号“0”的编码数字是2，而符号“=”的编码数字是6，那么对于简单公式“0=0”中的三个符号而言，编码数字就是2，6，2。把这三个数字作为前三个质数（2，3，5）的指数，得到如下数字：2²·3⁶·5²=72 900。

解码的过程，就是对大整数进行质数因子的分解（这是个唯一解），然后按顺序逐一读出每个质数底数的质数。

很大的整数与公式步调一致的移动

wff数（Well-formed formula）：以递归方式定义的特殊整数的集合，这些整数经由哥德尔的算法，代表了“形式良好”或“有意义”的PM定理，而不是那些无意义的或不合语法的符号串。

因为PM中较长的wff都是根据一些简单而标准化的排印并置规则从较短的wff中搭建起来的，所以与它们对应的较大的编码数字也同样可以根据简单而标准化的数字运算法则，从较小的编码数字中求得。

在罗素和怀特海眼中看起来精妙而复杂的符号调度，在库尔特·哥德尔的眼中看来则是大量的直白的数字运算处理。它们只不过是对于同一事件的不同看法而已，这两种看法完全是对等的，可以互相替换。

质雅数

有一类以递归方式定义的自然数，其中的数字对应的是PM的可证公式（即定理），在此将称它们为质雅数。

在罗素和怀特海的形式系统中，每一个可证公式都有一个相应的质雅数。每一个属于质雅数的整数都可以解码出符号，而你得到的符号串便是一个在PM中可证的公式。

PM的推演规则有时候会产生比输入串更短的输出串，这就意味着，定义质雅数的相应算术法则，有时会允许在输入一个大的质雅数后，输出的是一个更小的质雅数。

格鲁大师：

制造一台机器（给它起名叫“格鲁大师”），它总能正确回答任何以“n是一个质雅数吗？”的形式提出的问题。

那么，这位格鲁大师，可以凭一己之力，回答出你感兴趣的任何一个数论问题。
假设你想知道，陈述X是真的还是假的。你只需要把陈述X用PM的形式符号写下来，然后把得到的公式转换成它的哥德尔配数x，再把那个数字递给格鲁大师，询问x是否为一个质雅数。

怪圈

公式：“某个特定的整数g不是质雅数”。其中，g是这个公式的编码数字。
又可以直白地表达为：“我不可证”。

这个环路的怪异来自一个系统“吞食自我”的方式，即通过一种意料之外的回路扭转，粗暴地违反被我们认定为不可侵犯的等级秩序。

同样怪异和扭曲的（有真有假的）关于自己的论断：

• 我和我的否定命题都不是PM的定理；
• 如果我在PM内部有一个证明，那么我的否定命题便有一个比我更短的证明；
• 等等。

论向下的因果性

库尔特·哥德尔的那个怪圈公式，揭示出了一个令人咂舌的事实，即一个公式隐藏的意义也许拥有一种“向下”的因果力量来决定这个公式的真假。
如此，则人们不需要再以故有的方式推导公式的真假，即按章守法地从公理出发，“自下而上”地艰苦跋涉，而是仅仅通过了解公式的意义，就可以推断出它的真假了。

我的“我”，捉摸不定的心头肉

在人类本性的最深处，有一个由抽象模式构成的世界这些模式包括：“快餐”和“番茄蛤汁”、“黏性”和“古怪”、“反馈”和“公平竞争”、“目标”和“谎言”、“恐惧”和“梦想”、“你”和“我”。这些词汇在你我心中所指示的概念，乃是在我们各自大脑中所对应的符号。

你认为这些词汇确实表达了精确的定义，那么请深思一下：“雪”究竟是什么意思？它是如“将军”或“质数”一样清晰的范畴吗？比诸如“电子有1/2自旋”更加真实吗？

我们是相对宏观的存在，因此绝大多数人都从不会直接看见或应对电子或电磁感应定律。我们的感知聚焦在更大、更模糊的事物之上。我们内心深处更加信任宏观事物以及表面观察到的因果关系，而不是微观世界的电子作用。

“我”是我的大脑的最复杂的符号：一个大脑同一个闹壳（以及PM）一样，也可以（至少）在两个层面上接受观察：一个包括了很小的物理过程（可能是包括了粒子，也可能是包括了神经元——随你任选）的低级层面，和一个包括了由感知选择性触发的宏大结构的高级层面。后者在本书中被称为符号，其在我们的大脑中构成了“我”的范畴的结构。

大量被我们称为“我”的东西，在某个特定的时间，共同引发了某个特定的外部动作。
很快，我们的行动带来的数不清的后果开始向我们反弹回来，上百万的微小反射信号从外部冲击着我们，不论是在视觉上、听觉上、触觉上或者是任何感知层面，当它们在我们的大脑内落地时，都能激发起二级、三级的内部波纹。
最终，从这一簇凌乱的符号中筛选出一小把激活的符号（很小的一套精挑细选出来的范畴），便构成了对于我们刚刚所做之事的粗线条的理解。
这些反馈一旦以符号激活的形式被吸收，就会引发“我”的一次极小的修订。
由此一轮接着一轮，日日不息，年年不止。作为我们最内部的实质而发挥作用的这一抽象结构，正是以此方式，经由符号激发行动并反过来触发符号的环路，才得以缓慢而笃定地发生进化，并由此把自己比以往更严格地锁定在了我们的思维之中。

正是从原始刺激到符号的向上跃迁，为这个环路注入了“怪性”。由怪圈构成一个人的“我”的“稳定涡旋”。

“我”是一个真实的东西吗？一个类比是，我在装信封的箱子里发现的“玻璃球”是真实的吗？因为它囊括了我们在这个世界上感知到的因果性的真正重要的方面，并且如此整洁与高效，所以我们没办法不为我们的“我”以及其他人的“我”赋予真实性。

观者的“我”中的怪性

怪圈的第一种关键成分：一个视频系统，不管其具有多少像素或色彩，都绝不可能生成任何符号，因为视频系统不会感知。我们则可以。

怪圈的第二种关键成分：我们都无法以任何方式看到、感知到或察觉到构成我们思维底部的那些微观物质激烈狂热的蒸腾与翻滚。

缠结

大脑中的多重怪圈：
在每个人类的大脑中，都有一个怪圈，那个怪圈构成了我们的“我”，这只不过是粗糙的第一步假设。
既然我们在自己的大脑中都在以水平迥异的细节和忠实度来感知并表征着数百个其他的人类，既然所有那些人类最重要的面向就是他们自己对于自身的认识，那么我也无可避免地要在我们的头脑中反映并容纳数量巨大的其他怪圈。
而且，每一个人的头脑都是多重的“我”。涉及到熟悉的其他的人类时，会为我们自己的怪圈搭配了成千上万独特成分的装饰，新形成了一个结构非常丰富的“怪圈”。

我们如何活在彼此之中

概念是大脑中活跃的符号，跟其他认知对象一样，人在大脑中也是通过符号得到表征的。一个自我也是一个概念，只不过是一个更加复杂的概念。你的大脑也在不同的程度上容纳了其他的“我”、其他的灵魂，其程度取决于你对它的表征有多么忠实，以及你与目标个体形成了多么深刻的共鸣。

意识=思考

意识是闹壳内部的符号之舞。或者，甚至还可以更加简洁扼要地说，意识就是思考。

论宽宏与友谊

关于“我”的认识，且仅当与这个自我存在情感联系的其他自我伴随这个自我存在时，它才会存在。简言之，有宽容，才有自我。

困境

我们的困境如下：
我们要么相信，我们的意识是某种有别于物理法则产物的东西；
要么相信，它就是物理法则的产物。
但是，无论做出哪种选择，我们都会被引向令人困扰的，也许甚至难以接受的结论。

二元论观点认为，在由物理法则支配的物理实体之上，还存在一种名为“意识”的实体，它在宇宙中是隐形的、无法测量的、难以察觉的。这个概念颇具吸引力，因为它符合我们的日常经验，把世界一分为二，划分出有生命的和无生命的两种事物。
二元论是会引出一长串无法回答的问题。这些问题表明，二元论充斥着武断和不连贯性，看起来其自己的重量就足以把自己压垮了。

反过来，相信意识是物理法则的产物。这对于拥有科学头脑的人来说是很有吸引力的，因为它远比二元论简单得多。
它摆脱了平凡的物理实体和超凡的非物理实体之间令人迷惑的二分法，而那个围绕非物理性实体的本性而提出的绵长的问题清单也因此一笔勾销了。

自我和灵魂也从由无生命物质组成的基底上奇迹般地现身：
在最高的、最具集合性的层级上看，一个大脑是绝对有生命和有意识的。
当视角逐渐降低，结构逐层下降，从大脑到皮层、从神经柱到神经元，从细胞质到蛋白质，再从肽到粒子，生命的感觉逐渐消失，直到最低的层级，生命的痕迹已经完全不见了。
生命力的在场或缺席取决于人们在何种层级上观看一个结构。

有生命的实体是那些在某个描述层级上表现出特定类型的环路模式：
而当一个系统拥有通过知觉把世界过滤成不同范畴的内在能力，并精力十足地不断向抽象的层面扩大它的范畴库时，这种环路模式将不可避免地开始生成。
当根深蒂固的自我表征“实体给自己讲的故事”出现时，这种模式也就完全成熟了，由实体的“我”在其中担任主角，在一系列欲望的驱动下形成一个统一的因果主体。
一个实体拥有生命的程度，取决于这种环路“我”的模式的存在性，这不是一件有或无的事。

我们相信那些玻璃球，虽然当我们搜寻它们的时候，它们会消解不在，但是当我们不去寻找它们时，它们却和任何一颗真正的玻璃球一样真实。
我们人类静静地安处于非可视化的宇宙尺度的曲线时空与含糊不清、影影绰绰的带电粒子之间的某个中间地带，更像彩虹和海市蜃楼，而不是雨滴或岩石。