二分答案
首先我们看这个图:
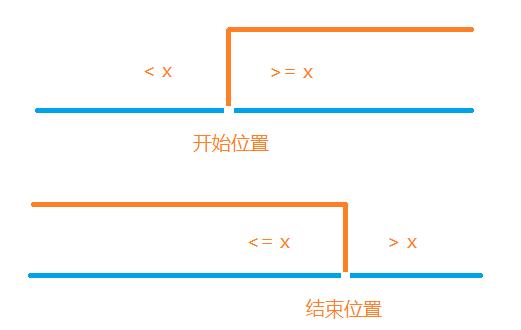
我们需要二分的答案就是这个临界点x。
什么情况下可以使用二分呢:
具有单调性(单调递增,单调递减),二段性(整个区间一分为二,一段区间满足,一段区间不满足),那个点x就是我们需要二分寻找的点。
二分的模板:
1. 图中第一种情况:
mid=(l+r)/ 2;,if ( check(mid ) )r=mid,l=mid+1;
2.图中第二种情况:
mid=(l+r+1) / 2, if ( check(mid ) )l=mid,r=mid-1;
//写check ,满足与不满足分别更新哪个区间;
// 二分一定可以二分出满足性质的数,但是结果需要判断是否符合性质;
例题:点击跳转例题
代码:#include <bits/stdc++.h> #define int long long //(有超时风险) #define PII pair<int,int> #define endl '\n' #define LL __int128 using namespace std; const int N=2e5+10,M=1e3+10,mod=998244353,INF=0x3f3f3f3f; int a[N],b[N],c[N],pre[N]; signed main() { std::ios::sync_with_stdio(false); std::cin.tie(nullptr); int n,q;cin>>n>>q; for(int i=0;i<n;i++) cin>>a[i]; while(q--) { int x;cin>>x; //注意r不能开大了,不然会超出数组的值,这样check数组外的值为0就会出错 int l=0,r=n-1; while(l<r) { //二段性:这个点后面的部分都满足 //用图一第一套模板 int mid=(l+r)/2; if(a[mid]>=x)r=mid; else l=mid+1; } if(a[l]!=x) cout<<"-1 -1"<<endl; else { cout<<l<<' '; int l=1,r=n-1; while (l<r) { //二段性:这个点前面的部分都满足 //用图一第二套模板 int mid=(l+r+1)/2; if(a[mid]<=x)l=mid; else r=mid-1; } cout<<l<<endl; } } return 0; }
二分算法--模板及原理总结
news2026/2/13 16:46:47
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1439181.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
嵌入式学习之Linux入门篇笔记——7,Linux常用命令第二部分
配套视频学习链接:http://【【北京迅为】嵌入式学习之Linux入门篇】 https://www.bilibili.com/video/BV1M7411m7wT/?p4&share_sourcecopy_web&vd_sourcea0ef2c4953d33a9260910aaea45eaec8
目录 1.mkdir 命令
2.rmdir
3.rm 命令
4.touch 命令
5.clear…
【Git教程】(一)基本概念 ——工作流、分布式版本控制、版本库 ~
Git教程 基本概念 1️⃣ 为什么要用 Git2️⃣ 为什么要用工作流3️⃣ 分布式版本控制4️⃣ 版本库5️⃣ 简单的分支创建与合并🌾 总结 在本章中,将介绍一个分布式版本控制系统的设计思路,以及它与集中式版本控制系统的不同之处。除此之外&am…
服务器运存使用率多少正常?
服务器运存使用率多少正常,这是一个相对主观的问题,因为服务器的正常运行不仅取决于运存使用率,还与服务器的工作负载、应用程序的特性和需求、服务器的配置和用途等多种因素有关。然而,一般来说,大多数服务器在运存使…
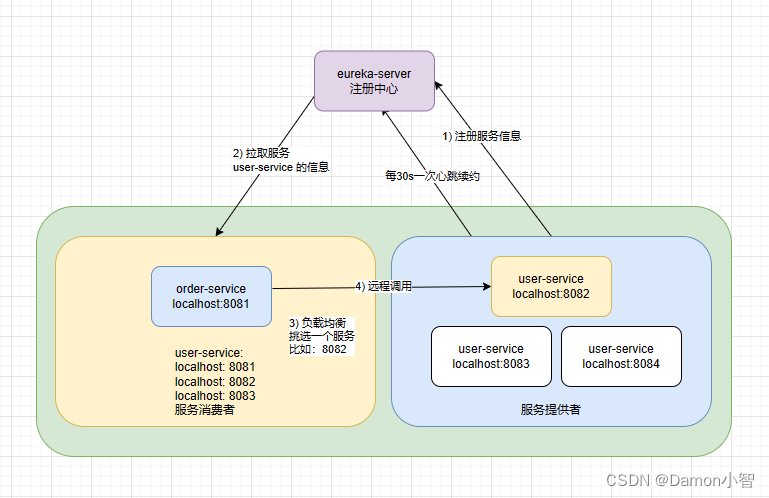
SpringCloud-Eureka原理分析
Eureka是Netflix开源的一款用于实现服务注册与发现的工具。在微服务架构中,服务的动态注册和发现是必不可少的组成部分,而Eureka正是为了解决这一问题而诞生的。
一、为何需要Eureka
在微服务架构中,服务之间的协同合作和高效通信是至关重要…
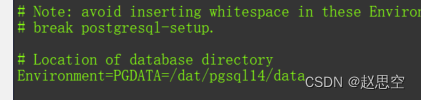
PostgreSql与Postgis安装
POstgresql安装
1.登录官网 PostgreSQL: Linux downloads (Red Hat family)
2.选择版本
3.安装
### 源
yum install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-7-x86_64/pgdg-redhat-repo-latest.noarch.rpm
### 客户端
yum install postgresql14
###…
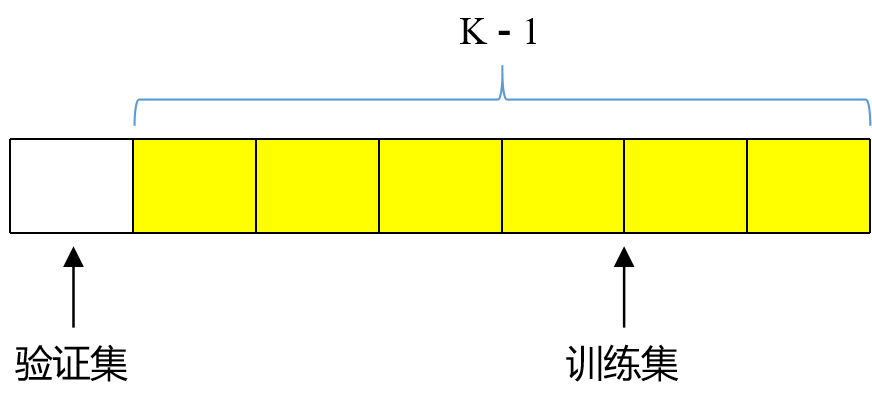
机器学习:数据集划分笔记
数据集划分是机器学习中非常关键的步骤,能直接影响模型的训练效果和泛化能力。它的主要目的是为了评估模型对新数据的泛化能力,即模型在未见过的数据上能表现良好。 数据集通常被划分为三个部分:训练集(Training set)、…
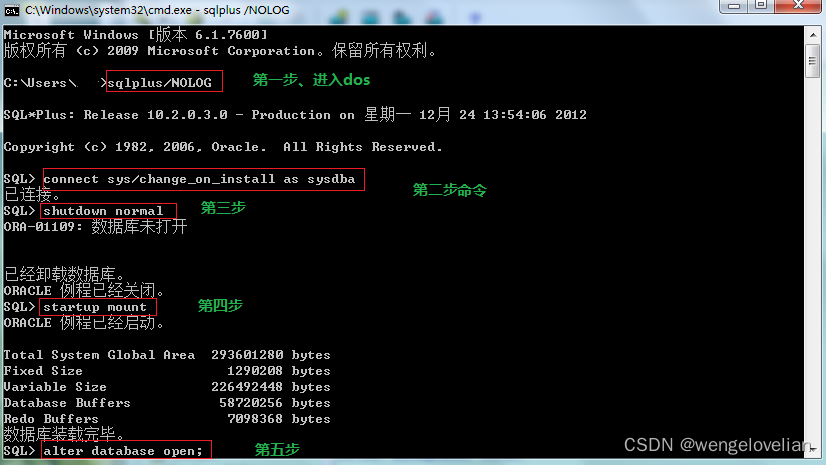
oracle 启动命令以及ORA-01033问题处理、删除归档日志
1 启动数据库:startup
2 关闭数据库:Shutdown immediate
3 查看监听状态:lsnrctl status
4 启动监听:lsnrctl start
5 停止监听:lsnrctl stop
常见问题
1、在服务器重启后会出现,Oracle ORA-01033: ORAC…
CPP项目:Boost搜索引擎
1.项目背景
对于Boost库来说,它是没有搜索功能的,所以我们可以实现一个Boost搜索引擎来实现一个简单的搜索功能,可以更快速的实现Boost库的查找,在这里,我们实现的是站内搜索,而不是全网搜索。
2.对于搜索…
单片机接收PC发出的数据
#include<reg51.h> //包含单片机寄存器的头文件 /***************************************************** 函数功能:接收一个字节数据 ***************************************************/ unsigned char Receive(void) { unsigned char dat; …
Hadoop搭建(完全分布式)
节点分布:
bigdata-masterbigdata-slave1bigdata-salve2 NameNode NodeManager NodeManager SecondaryNameNodeDataNodeDataNodeResourceManagerNodeManagerDataNode
目录
一、jdk安装:
二、hadoop安装 一、jdk安装:
jdk-8u212链接&am…
03-抓包_封包_协议_APP_小程序_PC应用_WEB应用
抓包_封包_协议_APP_小程序_PC应用_WEB应用 一、参考工具二、演示案例:2.1、WEB应用站点操作数据抓包-浏览器审查查看元素网络监听2.2、APP&小程序&PC抓包HTTP/S数据-Charles&Fiddler&Burpsuite2.3、程序进程&网络接口&其他协议抓包-WireSh…
Logback - 日志框架
引言 在当今的企业级应用开发中,日志管理是一个不可或缺的部分。它不仅帮助我们进行错误跟踪,还能有效监控应用程序的运行状态,为性能优化提供数据支撑。Spring Boot作为一个简化Spring应用开发的框架,自带了强大的日志管理功能。…
pytorch训练指标记录之tensoboard,wandb
详解Tensorboard及使用教程_tensorboard怎么用-CSDN博客文章浏览阅读5.1w次,点赞109次,收藏456次。目录一、什么是Tensorboard二、配置Tensorboard环境要求安装三、Tensorboard的使用使用各种add方法记录数据单条曲线(scalar)多条曲线(scalars)直方图(hi…
如何找准用户真实需求,建立情感连接?
品牌如果想要长久发展,除了独特的理念以及过硬的产品质量外还需要一点,那就在于它能持续、正确的为用户创造生活幸福感。这满足了用户的真实需求,并与其产生了情感连接,从而让品牌有机会逐渐融入、改善用户的生活实现长期价值与口…
ctfshow——命令执行
文章目录 web 29——通配符*绕过web30——调用其他命令执行函数web 31——参数逃逸web 32-web 36——配合文件包含伪协议web 37-web 39——文件包含web 40—— web 29——通配符*绕过 i不区分大小写,直接?csystem(tac fl*.php); web30——调用其他命令执行函数 调用…
三天学会MySQL(十)数据库范式与表关系
目录
一.范式
1.简介
2.第一范式
3.第二范式
4.第四范式
5.范式总结
二.表关系
1.简介
2.一对多关系
3.一对一关系
4.多对多关系 一.范式
1.简介 什么是范式( NF NormalForm ) 范式是符合某一种设计要求的总结。 在数据库中表的设计&#…
休斯顿NASA太空机器人进入最后测试阶段,或可模拟人类执行外星任务!
美国宇航局开发研制的太空智能机器人目前正在德州休斯顿的约翰逊航天中心接受最后的运行测试,距离太空智能化时代又要更进一步了! NASA表示,日前在德州休斯顿附近的约翰逊航天中心进行测试的机器人名为Valkyrie,是以北欧神话中的一…
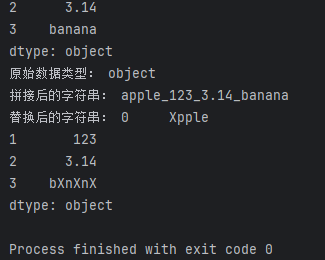
Pandas文本数据处理大全:类型判断、空白字符处理、拆分与连接【第67篇—python:文本数据】
文章目录 Pandas文本数据处理大全:类型判断、空白字符处理、拆分与连接1. 判断文本数据类型2. 去除空白字符3. 文本数据拆分4. 文本数据连接5. 文本数据替换6. 文本数据匹配与提取7. 文本数据的大小写转换8. 文本数据的长度计算9. 文本数据的排序10. 文本数据的分组…