数据集划分是机器学习中非常关键的步骤,能直接影响模型的训练效果和泛化能力。它的主要目的是为了评估模型对新数据的泛化能力,即模型在未见过的数据上能表现良好。
数据集通常被划分为三个部分:训练集(Training set)、验证集(Validation set)和测试集(Test set)。

目录
原因
1.避免过拟合
2.模型评估
3.模型选择和调参
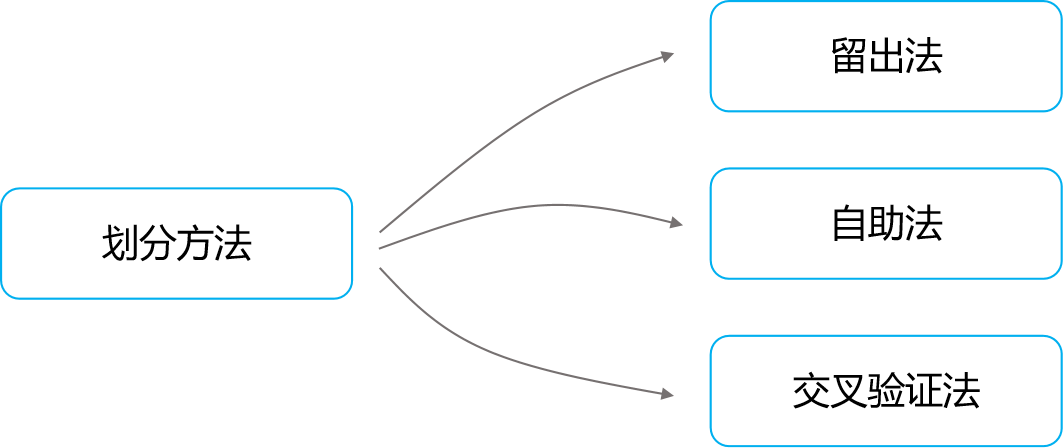
方法
1.留出法(Hold-out Method)
2.自助法(Bootstrap Method)
3.交叉验证法(Cross-Validation Method)
3.1 K-Fold 交叉验证(K-Fold Cross-Validation)
3.2 留一法交叉验证(Leave-One-Out Cross-Validation)
3.3 分层K-Fold 交叉验证(Stratified K-Fold Cross-Validation)
3.4 分组交叉验证(Group K-Fold Cross-Validation)
应用
1.留出法——train_test_split函数
2.自助法——resample函数
3.交叉验证法——KFold或StratifiedKFold类
注意事项
1.数据泄露
2.数据不平衡
3.数据的代表性
原因
1.避免过拟合
过拟合(Overfitting)是机器学习和统计学中的常见问题,表现为模型在训练集上的正确率显著高于验证集。通常是模型过于复杂或训练数据量太少,导致捕捉到了数据中的噪声和异常值,而不仅仅是底层的数据分布规律。
2.模型评估
机器学习需要一种可靠的方法来评估模型的预测能力和泛化能力。其中验证集用于初步评估模型的性能,而测试集用于最终评估模型的泛化能力(即模拟真实世界的应用场景)。
3.模型选择和调参
训练集和验证集能帮助研究者在机器学习项目的开发过程中选择最佳模型和调整参数,以提高模型的性能。
方法
1.留出法(Hold-out Method)
一种简单直观的数据集划分方法,它将数据集分为两个互斥的集合,即训练集和测试集。有时候,为了进行模型选择和调参,还会从训练集中进一步留出一部分数据作为验证集。这种方法的关键在于保持数据的独立性和分布的一致性,避免信息泄露和过拟合。
优点:
- 操作简单,易于实现。
- 分离的测试集可以提供对模型性能的无偏估计。
缺点:
- 数据的划分可能会导致训练集和测试集的分布不一致。
- 在数据量较少的情况下,留出大部分数据作为训练集可能会导致测试集较小,评估结果的方差较大。
- 模型的评估结果极度依赖于数据的划分方式。
2.自助法(Bootstrap Method)
一种有放回的抽样方法,用于从原始数据集中生成多个训练集的技术,适用于样本量不足时的模型评估。在自助法中,我们从原始数据集中随机选择一个样本加入到训练集中,然后再把这个样本放回原始数据集,允许它被再次选中。这个过程重复n次,n是原始数据集中的样本数量。这样,一些样本在训练集中会被重复选择,而有些则可能一次也不被选中。未被选中的样本通常用作测试集。
优点:
- 在数据量有限的情况下,自助法可以有效地增加训练数据的多样性。
- 对于小样本数据集,自助法可以提供更加稳定和准确的模型评估。
- 可以用来估计样本的分布和参数的置信区间。
缺点:
- 由于采样是有放回的,可能导致训练集中的某些样本被多次选择,而有些样本则从未被选择,这可能会引入额外的方差。
- 对于足够大的数据集,自助法可能不如其他方法,如 K-Fold 交叉验证,因为重复的样本可能导致评估效果不是很好。
3.交叉验证法(Cross-Validation Method)
通过将数据集分成多个小子集,反复地进行训练和验证过程,以此来减少评估结果因数据划分方式不同而带来的偶然性和不确定性。以下是几种常见的交叉验证方法:
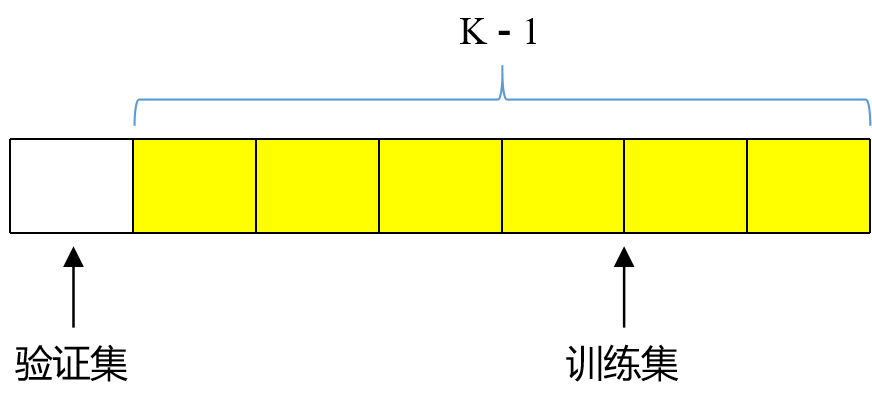
3.1 K-Fold 交叉验证(K-Fold Cross-Validation)
把数据集平均划分成 K个大小相等的子集,对于每一次验证,选取其中一个子集作为验证集,而其余的 K-1个子集合并作为训练集。这个过程会重复K次,每次选择不同的子集作为验证集。最后,通常取这K次验证结果的平均值作为最终的性能评估。适用于数据集不是非常大的情况。
- 优点:减少了评估结果因数据划分不同而产生的偶然性,提高了评估的准确性和稳定性。
- 缺点:计算成本高,尤其是当K值较大或数据集较大时。
3.2 留一法交叉验证(Leave-One-Out Cross-Validation)
留一法是 K-Fold 交叉验证的一个特例,其中K等于样本总数。这意味着每次只留下一个样本作为验证集,其余的样本作为训练集。这个过程重复进行,直到每个样本都被用作过一次验证集。
- 优点:可以最大限度地利用数据,每次训练都使用了几乎所有的样本,这在样本量较少时尤其有价值。
- 缺点:计算成本非常高,尤其是对于大数据集来说,几乎是不可行的。
3.3 分层K-Fold 交叉验证(Stratified K-Fold Cross-Validation)
分层K-Fold 交叉验证是对 K-Fold 交叉验证的一个改进,特别适用于处理类别不平衡的数据集。在这种方法中,每次划分数据时都会保持每个类别的样本比例,确保在每个训练集和验证集中各类的比例与整个数据集中的比例大致相同。
- 优点:对于分类问题,可以保持类别比例,提高模型的泛化能力。
- 缺点:实现相对复杂,需要根据数据的具体类别分布来进行样本的分层抽样。
3.4 分组交叉验证(Group K-Fold Cross-Validation)
分组交叉验证是处理具有明显组结构数据的交叉验证策略。该方法的关键在于确保来自同一组的数据在分割过程中不会被分散到不同的训练集或测试集中。特别适用于数据中存在自然分组的情况,如医学领域(按病人分组)、
原理:
假设我们的数据集中有若干个组,每个组包含多个观察(或样本)。在分组交叉验证中,数据不是随机分成K个子集,而是根据组的标识来分。整个数据集被分为K个子集,但划分的依据是组而不是单个样本。每一次迭代中,选定的一个或多个组整体作为测试集,其余的组作为训练集。这个过程重复进行,直到每个组都有机会作为测试集。
示例:
假设我们有一个医疗影像数据集,这个数据集包含来自100个不同病人的MRI扫描图像。每个病人的图像数量不同,但我们知道哪些图像属于同一个病人。如果我们的目标是开发一个模型,用于根据新病人的MRI图像预测某种疾病的存在,那么在训练和验证模型时,我们需要确保来自同一病人的图像要么全部在训练集中,要么全部在测试集中。这样做的原因是避免模型仅仅因为学习了某个病人图像的特定特征(而不是疾病的普遍特征)而表现出看似良好的性能。
在分组交叉验证中,我们首先将数据按病人分组(即每个组是一个病人的所有图像)。如果我们选择进行 5-fold 交叉验证,那么数据集将被分为5个子集,每个子集包含大约20个病人的所有图像。在验证过程的每一步中,我们选择其中一个子集作为测试集(包含20个病人的图像),剩余的子集(包含其余80个病人的图像)合并作为训练集。这个过程重复5次,每次都更换测试集,以确保每个病人的图像都有机会用于验证模型。
优点:
- 避免数据泄露:确保模型评估不会受到来自同一组但不同样本的数据相似性的影响。
- 更准确的泛化能力评估:通过模拟真实场景(即,对未见过的组进行预测)的方式,更准确地评估模型对新数据的处理能力。
缺点:
- 实现复杂性:需要有明确的组标识,且在数据划分时要根据这些组标识来进行。
- 可能的样本不均衡:如果各组的大小差异很大,可能导致训练和测试集的样本分布不均。
应用
在Python中,主要通过 scikit-learn库 来实现数据划分,该库提供了一系列的函数和类来支持不同的数据划分方法。以下是几种常用的数据集划分方法的Python实现:
1.留出法——train_test_split函数
from sklearn.model_selection import train_test_split
# 假设X是特征,y是标签
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=2024)测试集:训练集 = 2:8。
2.自助法——resample函数
from sklearn.utils import resample
# 假设X是特征,y是标签
X_bootstrap, y_bootstrap = resample(X, y, replace=True, n_samples=len(X), random_state=2024)通过有放回的抽样,创建了一个新的 训练集X_bootstrap 和对应的 标签y_bootstrap。
3.交叉验证法——KFold或StratifiedKFold类
from sklearn.model_selection import KFold
kf = KFold(n_splits=5, shuffle=True, random_state=2024)
for train_index, test_index in kf.split(X):
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]n_splits=5表示分成5份,shuffle=True确保了数据在分割前会被随机打乱。
注意事项
1.数据泄露
在划分数据集时,要确保测试集(有时也包括验证集)中的信息在训练阶段对模型完全不可见,避免数据泄露导致评估结果不准确。
2.数据不平衡
对于不平衡的数据集,需要特别注意采用分层抽样等技术,确保每个类别的样本在各个子集中都有合理的分布。
3.数据的代表性
数据集划分后,需要确保训练集、验证集和测试集在统计特性上都能代表整个数据集,避免由于数据划分导致的偏差。







![最大子数组和[中等]](https://img-blog.csdnimg.cn/direct/054d660177f04abab28f0fc0af6ae8bc.png)