题目描述

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

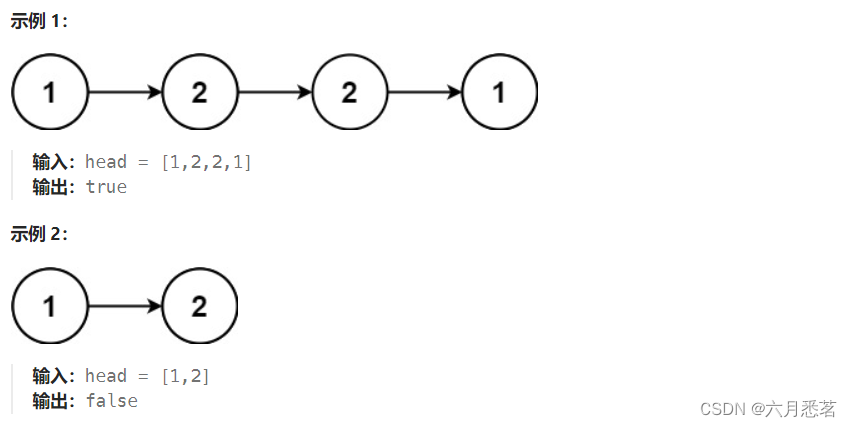
提示：
链表中节点数目在范围[1, 100000] 内
0 <= Node.val <= 9

方法一：将值复制到数组中后用双指针法

思路

如果你还不太熟悉链表，下面有关于列表的概要讲述。

有两种常用的列表实现，分别为数组列表和链表。如果我们想在列表中存储值，它们是如何实现的呢？

数组列表底层是使用数组存储值，我们可以通过索引在 O(1) 的时间访问列表任何位置的值，这是由基于内存寻址的方式。
链表存储的是称为节点的对象，每个节点保存一个值和指向下一个节点的指针。访问某个特定索引的节点需要 O(n) 的时间，因为要通过指针获取到下一个位置的节点。
确定数组列表是否回文很简单，我们可以使用双指针法来比较两端的元素，并向中间移动。一个指针从起点向中间移动，另一个指针从终点向中间移动。这需要 O(n) 的时间，因为访问每个元素的时间是 O(1)，而有 n 个元素要访问。

然而同样的方法在链表上操作并不简单，因为不论是正向访问还是反向访问都不是 O(1)。而将链表的值复制到数组列表中是 O(n))，因此最简单的方法就是将链表的值复制到数组列表中，再使用双指针法判断。

算法

一共为两个步骤：

复制链表值到数组列表中。
使用双指针法判断是否为回文。
第一步，我们需要遍历链表将值复制到数组列表中。我们用 currentNode 指向当前节点。每次迭代向数组添加 currentNode.val，并更新 currentNode = currentNode.next，当 currentNode = null 时停止循环。

执行第二步的最佳方法取决于你使用的语言。在 Python 中，很容易构造一个列表的反向副本，也很容易比较两个列表。而在其他语言中，就没有那么简单。因此最好使用双指针法来检查是否为回文。我们在起点放置一个指针，在结尾放置一个指针，每一次迭代判断两个指针指向的元素是否相同，若不同，返回 false；相同则将两个指针向内移动，并继续判断，直到两个指针相遇。

在编码的过程中，注意我们比较的是节点值的大小，而不是节点本身。正确的比较方式是：node_1.val == node_2.val，而 node_1 == node_2 是错误的。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
// 判断给定的单链表是否为回文链表的函数
bool isPalindrome(struct ListNode* head) {
    // 定义一个数组 vals 用于存储链表节点的值，数组大小为 50001
    int vals[50001];
    // 定义一个变量 vals_num 用于记录数组中元素的个数，初始化为 0
    int vals_num = 0;

    // 遍历链表，将链表节点的值存储到数组 vals 中
    while (head != NULL) {
        // 将当前链表节点的值存储到数组 vals 中，并更新 vals_num
        vals[vals_num++] = head->val;
        // 移动到链表的下一个节点
        head = head->next;
    }

    // 使用双指针从数组 vals 的两端向中间遍历，比较对应位置的值是否相等
    // 注意这里只用了一个循环，本来想用双循环，但是双循环的话没有办法首尾对应
    for (int i = 0, j = vals_num - 1; i < j; ++i, --j) {
        // 如果对应位置的值不相等，则链表不是回文链表，返回 false
        if (vals[i] != vals[j]) {
            return false;
        }
    }
    // 如果双指针都遍历到了中间，且对应位置的值都相等，则链表是回文链表，返回 true
    return true;
}

复杂度分析

时间复杂度： O(n)，其中 n 指的是链表的元素个数。
第一步： 遍历链表并将值复制到数组中，O(n)。
第二步：双指针判断是否为回文，执行了 O(n/2) 次的判断，即 O(n)。
总的时间复杂度：O(2n)=O(n)。
空间复杂度：O(n)，其中 n 指的是链表的元素个数，我们使用了一个数组列表存放链表的元素值。

方法二：递归

思路

为了想出使用空间复杂度为 O(1) 的算法，你可能想过使用递归来解决，但是这仍然需要 O(n) 的空间复杂度。

递归为我们提供了一种优雅的方式来方向遍历节点。

function print_values_in_reverse(ListNode head)
    if head is NOT null
        print_values_in_reverse(head.next)
        print head.val

如果使用递归反向迭代节点，同时使用递归函数外的变量向前迭代，就可以判断链表是否为回文。

算法

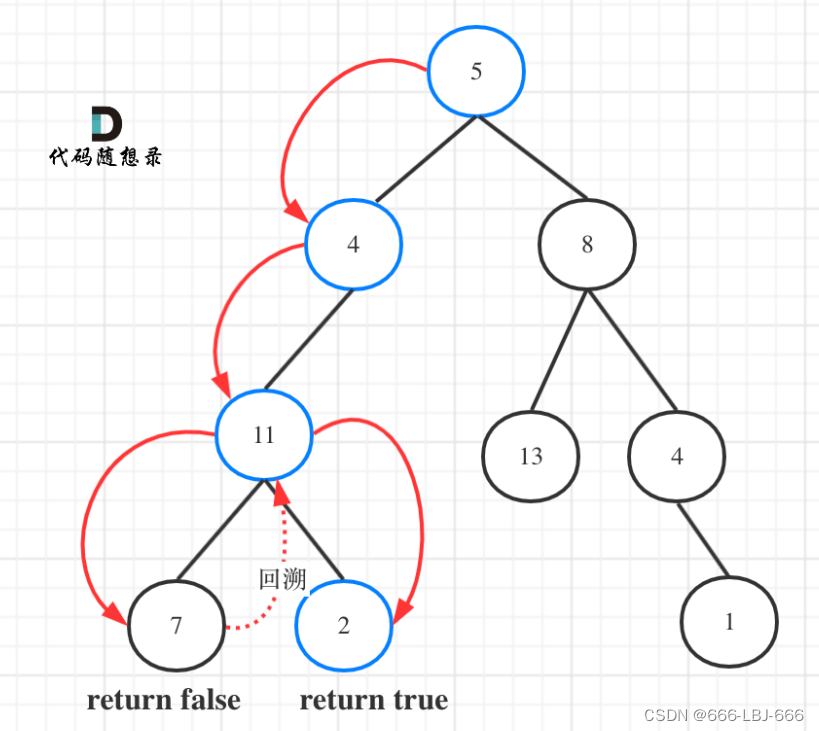
currentNode 指针是先到尾节点，由于递归的特性再从后往前进行比较。frontPointer 是递归函数外的指针。若 currentNode.val != frontPointer.val 则返回 false。反之，frontPointer 向前移动并返回 true。

算法的正确性在于递归处理节点的顺序是相反的（回顾上面打印的算法），而我们在函数外又记录了一个变量，因此从本质上，我们同时在正向和逆向迭代匹配。

计算机在递归的过程中将使用堆栈的空间，这就是为什么递归并不是 O(1) 的空间复杂度。

// 定义一个全局变量 frontPointer，用于记录当前链表节点的指针位置
struct ListNode* frontPointer;

// 递归检查函数，用于检查给定的单链表是否为回文链表
bool recursivelyCheck(struct ListNode* currentNode) {
    // 如果当前节点不为空
    if (currentNode != NULL) {
        // 递归调用 recursivelyCheck 函数，传入当前节点的下一个节点，检查链表后半部分是否为回文
        if (!recursivelyCheck(currentNode->next)) {
            return false; // 如果不是回文，则返回 false
        }
        // 如果当前节点的值与 frontPointer 所指向的节点的值不相等，则链表不是回文，返回 false
        if (currentNode->val != frontPointer->val) {
            return false;
        }
        // 将 frontPointer 指向下一个节点，继续向后比较
        frontPointer = frontPointer->next;
    }
    // 如果链表遍历完成且没有发现不同，则链表是回文，返回 true
    return true;
}

// 判断给定的单链表是否为回文链表的函数
bool isPalindrome(struct ListNode* head) {
    // 将全局变量 frontPointer 指向头节点，表示开始比较链表的头部
    frontPointer = head;
    // 调用递归检查函数，传入头节点，检查整个链表是否为回文
    return recursivelyCheck(head);
}

这段代码使用了一个全局变量 frontPointer，它指向当前需要比较的节点。函数 recursivelyCheck 通过递归的方式从链表的尾部开始向前比较节点的值，同时从链表的头部开始向后移动 frontPointer 指针，实现了对单链表的回文性质进行检查。函数 isPalindrome 是入口函数，用于调用递归检查函数并返回结果。

假设有一个单链表的结构如下所示：

1 -> 2 -> 3 -> 2 -> 1

这个链表是一个回文链表，因为正着读和倒着读都是相同的。

现在我们来看看代码是如何检查这个链表是否为回文链表的：

1. 初始化：

   • 首先，我们调用 isPalindrome(head) 函数，其中 head 指向链表的头部。
   • frontPointer 全局变量被初始化为指向链表的头部，表示我们从链表的头部开始比较。

2. 递归检查：

   • 递归调用 recursivelyCheck(head) 函数，其中 currentNode 为当前节点，开始时指向链表的头部。
   • 我们进入递归函数，先判断当前节点是否为 NULL，如果不是则继续执行。
   • 递归调用 recursivelyCheck(currentNode->next)，传入下一个节点，即 2 -> 3 -> 2 -> 1。
   • 递归调用继续，直到 currentNode 指向链表的最后一个节点 1。
   • 然后我们开始回溯，从链表的尾部向头部逐个比较节点的值，同时 frontPointer 从链表的头部向后移动。
   • 当 currentNode 指向 1 时，我们开始比较最后一个节点的值 1 和 frontPointer 指向的节点的值 1，它们相等，继续。
   • currentNode 指向 2，frontPointer 指向链表的头部，比较节点的值 2 和 1，不相等，返回 false。
   • 回溯过程中，如果有不相等的节点值，则直接返回 false。

复杂度分析

时间复杂度：O(n)，其中 n 指的是链表的大小。
空间复杂度：O(n)，其中 nnn 指的是链表的大小。我们要理解计算机如何运行递归函数，在一个函数中调用一个函数时，计算机需要在进入被调用函数之前跟踪它在当前函数中的位置（以及任何局部变量的值），通过运行时存放在堆栈中来实现（堆栈帧）。在堆栈中存放好了数据后就可以进入被调用的函数。在完成被调用函数之后，他会弹出堆栈顶部元素，以恢复在进行函数调用之前所在的函数。在进行回文检查之前，递归函数将在堆栈中创建 n 个堆栈帧，计算机会逐个弹出进行处理。所以在使用递归时空间复杂度要考虑堆栈的使用情况。
这种方法不仅使用了 O(n) 的空间，且比第一种方法更差，因为在许多语言中，堆栈帧的开销很大（如 Python），并且最大的运行时堆栈深度为 1000（可以增加，但是有可能导致底层解释程序内存出错）。为每个节点创建堆栈帧极大的限制了算法能够处理的最大链表大小。

方法三：快慢指针

思路

避免使用 O(n) 额外空间的方法就是改变输入。

我们可以将链表的后半部分反转（修改链表结构），然后将前半部分和后半部分进行比较。比较完成后我们应该将链表恢复原样。虽然不需要恢复也能通过测试用例，但是使用该函数的人通常不希望链表结构被更改。

该方法虽然可以将空间复杂度降到 O(1)，但是在并发环境下，该方法也有缺点。在并发环境下，函数运行时需要锁定其他线程或进程对链表的访问，因为在函数执行过程中链表会被修改。

算法

整个流程可以分为以下五个步骤：

1. 找到前半部分链表的尾节点。
2. 反转后半部分链表。
3. 判断是否回文。
4. 恢复链表。
5. 返回结果。

执行步骤一，我们可以计算链表节点的数量，然后遍历链表找到前半部分的尾节点。

我们也可以使用快慢指针在一次遍历中找到：慢指针一次走一步，快指针一次走两步，快慢指针同时出发。当快指针移动到链表的末尾时，慢指针恰好到链表的中间。通过慢指针将链表分为两部分。

若链表有奇数个节点，则中间的节点应该看作是前半部分。

步骤二可以使用「反转链表」问题中的解决方法来反转链表的后半部分。

步骤三比较两个部分的值，当后半部分到达末尾则比较完成，可以忽略计数情况中的中间节点。

步骤四与步骤二使用的函数相同，再反转一次恢复链表本身。

代码

// 反转单链表
struct ListNode* reverseList(struct ListNode* head) {
    // 初始化前一个节点指针为 NULL
    struct ListNode* prev = NULL;
    // 当前节点指针指向头节点
    struct ListNode* curr = head;
    // 遍历链表
    while (curr != NULL) {
        // 保存当前节点的下一个节点
        struct ListNode* nextTemp = curr->next;
        // 当前节点的 next 指针指向前一个节点
        curr->next = prev;
        // 更新 prev 指针为当前节点
        prev = curr;
        // 更新 curr 指针为下一个节点
        curr = nextTemp;
    }
    // 返回反转后的链表头节点
    return prev;
}

// 找到链表的前半部分的尾节点
struct ListNode* endOfFirstHalf(struct ListNode* head) {
    // 初始化快慢指针都指向头节点
    struct ListNode* fast = head;
    struct ListNode* slow = head;
    // 快指针每次移动两步，慢指针每次移动一步，直到快指针到达链表末尾
    while (fast->next != NULL && fast->next->next != NULL) {
        fast = fast->next->next;
        slow = slow->next;
    }
    // 返回慢指针指向的节点，即前半部分链表的尾节点
    return slow;
}

// 判断链表是否为回文链表
bool isPalindrome(struct ListNode* head) {
    // 如果链表为空，则是回文链表
    if (head == NULL) {
        return true;
    }

    // 找到前半部分链表的尾节点并反转后半部分链表
    struct ListNode* firstHalfEnd = endOfFirstHalf(head);
    struct ListNode* secondHalfStart = reverseList(firstHalfEnd->next);

    // 判断是否回文
    struct ListNode* p1 = head;
    struct ListNode* p2 = secondHalfStart;
    bool result = true;
    // 依次比较前半部分和后半部分链表的节点值
    while (result && p2 != NULL) {
        if (p1->val != p2->val) {
            result = false;
        }
        p1 = p1->next;
        p2 = p2->next;
    }

    // 还原链表并返回结果
    firstHalfEnd->next = reverseList(secondHalfStart);
    return result;
}

复杂度分析

时间复杂度：O(n)，其中 n 指的是链表的大小。

空间复杂度：O(1)。我们只会修改原本链表中节点的指向，而在堆栈上的堆栈帧不超过 O(1)。

作者：力扣官方题解
链接：https://leetcode.cn/problems/palindrome-linked-list/solutions/457059/hui-wen-lian-biao-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。