每日一练：LeeCode-112、路径总和【二叉树+DFS+回溯】

news2024/9/25 17:15:25

本文是力扣LeeCode-112、路径总和学习与理解过程，本文仅做学习之用，对本题感兴趣的小伙伴可以出门左拐LeeCode。

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点是指没有子节点的节点。

示例 1：
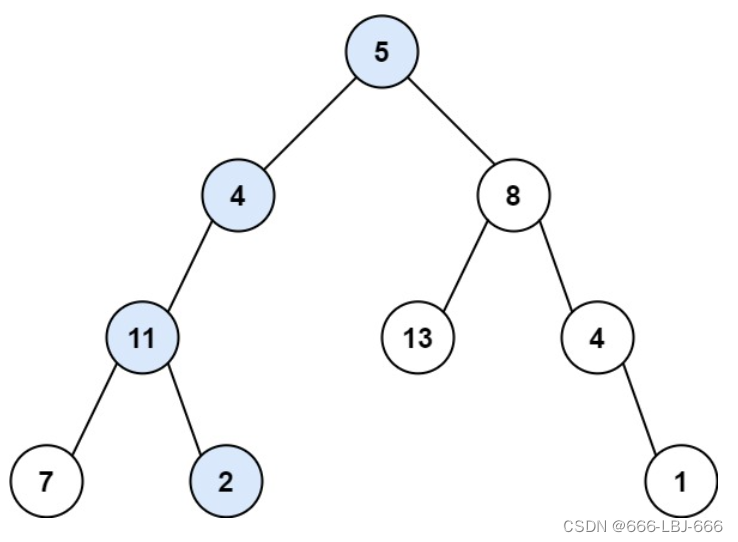
在这里插入图片描述

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：
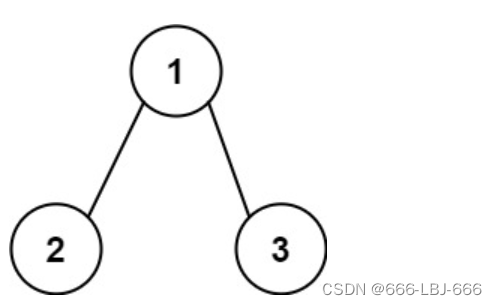
在这里插入图片描述

输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

思路

递归法

可以使⽤深度优先遍历的⽅式（本题前中后序都可以，⽆所谓，因为中节点也没有处理逻辑）来遍历⼆叉树

1. 确定递归函数的参数和返回类型

boolean bianLi(TreeNode root, int count)	//需要⼆叉树的根节点，还需要⼀个计数器

递归函数什么时候需要返回值？
如果需要搜索整棵⼆叉树且不⽤处理递归返回值，递归函数就不要返回值。
如果需要搜索整棵⼆叉树且需要处理递归返回值，递归函数就需要返回值。
如果要搜索其中⼀条符合条件的路径，那么递归⼀定需要返回值，因为遇到符合条件的路径了就要及时返回。

⽽本题我们要找⼀条符合条件的路径，所以递归函数需要返回值，及时返回，那么返回类型是什么呢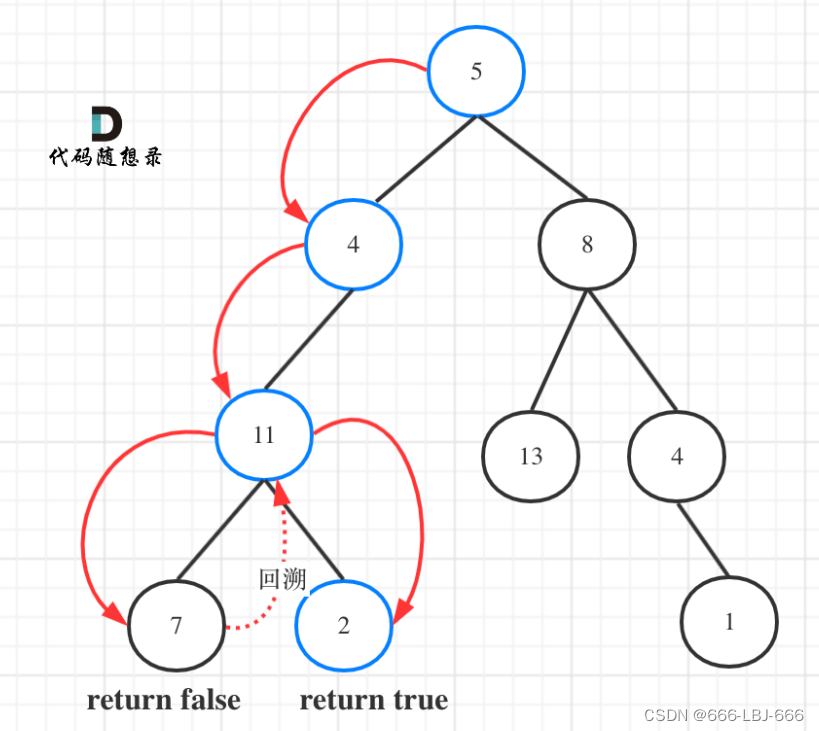？在这里插入图片描述
图中可以看出，遍历的路线，并不要遍历整棵树，所以递归函数需要返回值，可以⽤bool类型表示

2. 确定终⽌条件
⾸先计数器如何统计这⼀条路径的和呢？
不要去累加然后判断是否等于⽬标和，那么代码⽐较麻烦，可以⽤递减，让计数器count初始为⽬标和，然后每次减去遍历路径节点上的数值。
如果最后count == 0，同时到了叶⼦节点的话，说明找到了⽬标和。
如果遍历到了叶⼦节点，count不为0，就是没找到

 if(root.left==null&&root.right==null&&count==0)return true; // 遇到叶⼦节点，并且计数为0
 if(root.left==null&&root.right==null)return false; //遇到叶⼦节点⽽没有找到合适的边，直接返回

3. 确定单层递归的逻辑
因为终⽌条件是判断叶⼦节点，所以递归的过程中就不要让空节点进⼊递归了。
递归函数是有返回值的，如果递归函数返回true，说明找到了合适的路径，应该⽴刻返回。

        if(root.left!=null){
            count-=root.left.val;	// 递归，处理节点;
            if(bianLi(root.left,count))return true;// 遇到叶⼦节点返回true，则直接返回true
            count+=root.left.val;	// 回溯，撤销处理结果
        }
        if(root.right!=null){
            count-=root.right.val;	// 递归，处理节点;
            if(bianLi(root.right,count))return true;	// 遇到叶⼦节点返回true，则直接返回true
            count+=root.right.val;	// 回溯，撤销处理结果
        }

完整代码

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root==null)return false;
        return bianLi(root,targetSum-root.val);
    }

    boolean bianLi(TreeNode root, int count){
        if(root.left==null&&root.right==null&&count==0)return true;
        if(root.left==null&&root.right==null)return false;
        if(root.left!=null){
            count-=root.left.val;
            if(bianLi(root.left,count))return true;
            count+=root.left.val;
        }
        if(root.right!=null){
            count-=root.right.val;
            if(bianLi(root.right,count))return true;
            count+=root.right.val;
        }
        return false;
    }
}