1. 什么是前缀和算法

前缀和算法（Prefix Sum）是一种用于快速计算数组元素之和的技术。它通过预先计算数组中每个位置前所有元素的累加和，将这些部分和存储在一个新的数组中，从而在需要计算某个区间的和时，可以通过简单的减法操作得到结果，而不必重新遍历整个区间。

2. 一维前缀和

在这里我们通过一个例题来讲解：【模板】前缀和_牛客题霸_牛客网 (nowcoder.com)

题目描述如下

我们在一个数组中想要q次访问一段下标为 [l, r] 的数据和即

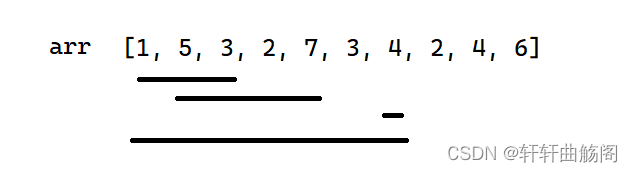
我们稍加分析可以发现，如果我们使用暴力解法（将区间内所有数字相加）时间复杂度为O(q*N)，在这里我们可以使用前缀和的算法，来使每次访问的时间复杂度降低到O(1)，在这里我们要提前预备好一个dp数组，dp[i]表示从下标1开始到下标i的数值和，dp[i] = dp[i-1] + arr[i]，这样填完dp表后，[l, r]的数值和sum = dp[r] - dp[l-1]，此外在这里有一个细节需要我们注意：下标为什么是从1开始的？——假如要计算[0, 2]的话，我们需要使用dp[2] - dp[-1]，这样就会带来不便。

我们可以得到这道题的代码

#include <iostream>
#include <vector>
using namespace std;

int main() 
{
    int n = 0, q = 0;
    cin >> n >> q;
    vector<int> arr(n + 1);
    for (int i = 1; i <= n; i++) cin >> arr[i];

    // 使用long long 避免整型溢出
    vector<long long> dp(n + 1);
    for (int i = 1; i <= n; i++) dp[i] = dp[i-1] + arr[i];

    int l = 0, r = 0;
    while (q--)
    {
        cin >> l >> r;
        cout << dp[r] - dp[l-1] << endl;
    }

    return 0;
}

3. 二维前缀和

在这里我们使用另一个例题：【模板】二维前缀和_牛客题霸_牛客网 (nowcoder.com)

在这里，我们需要得到从下标(x1, y1)->(x2, y2)所有数值和，我们同样可以使用前缀和来解决。二维的前缀和与一维的相似，我们可以规定dp[i][j]表示从下标(1, 1)->(i, j)所有数值和，我们要计算的dp[i][j]可以按如下方式计算

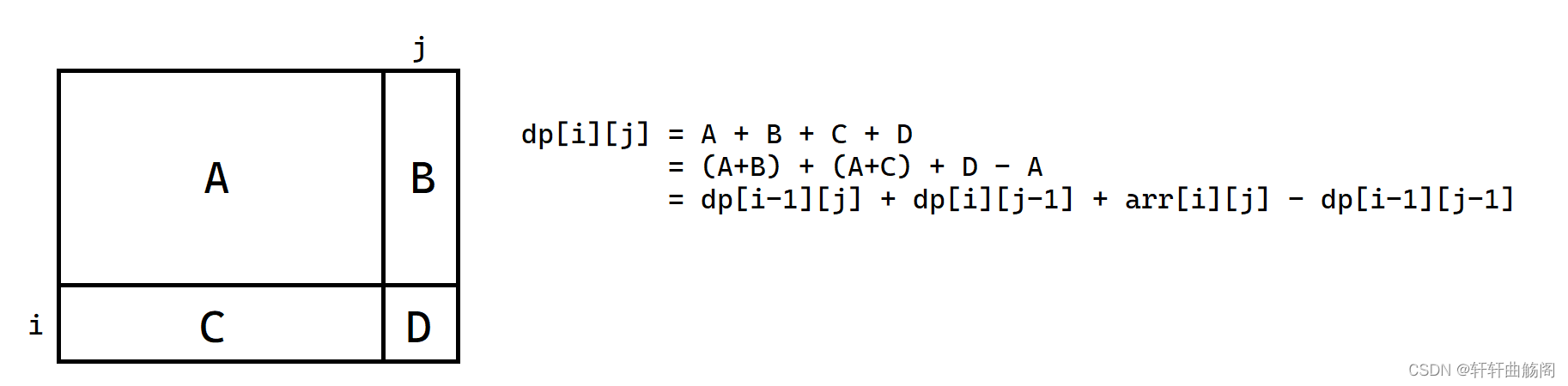
即dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1]，在预备好了dp数组过后，我们如何来使用它呢？图解如下

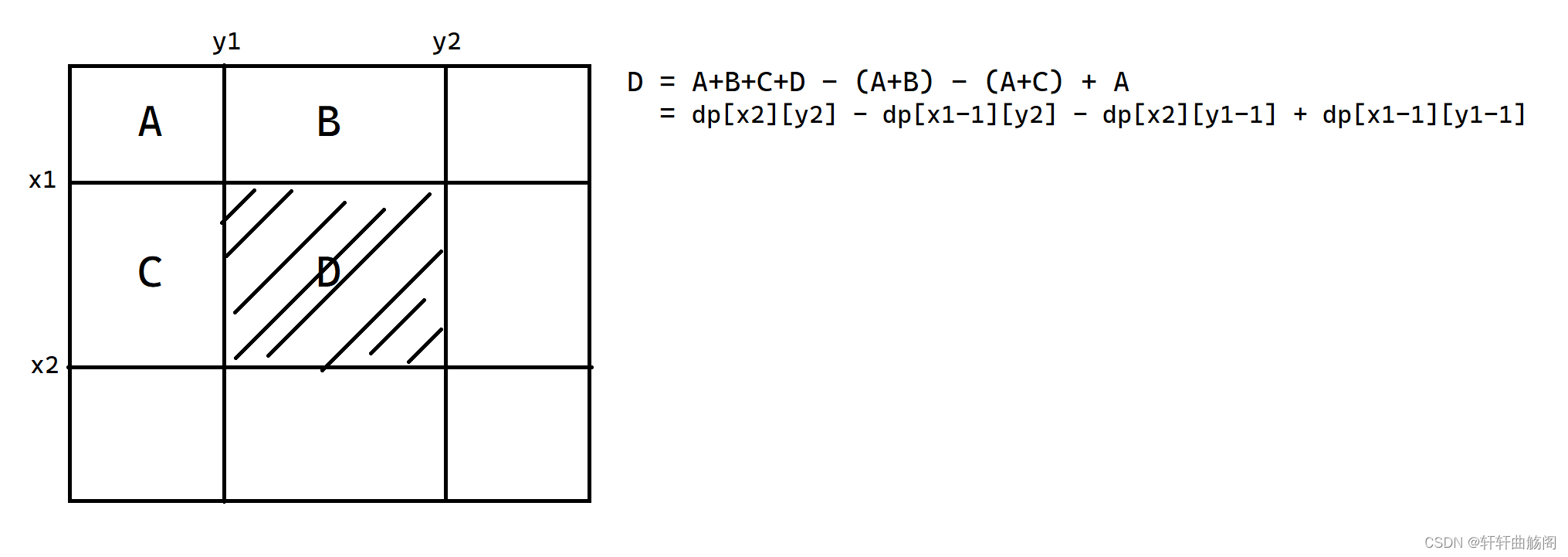
我们可以使用如下代码解决此问题

#include <iostream>
#include <vector>
using namespace std;

int main() 
{
    int n = 0, m = 0, q = 0;
    cin >> n >> m >> q;
    vector<vector<int>> arr(n + 1, vector<int>(m + 1));
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> arr[i][j];

    vector<vector<long long>> dp(n + 1, vector<long long>(m + 1));
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1];

    int x1 = 0, y1 = 0, x2 = 0, y2 = 0;
    while (q--)
    {
        cin >> x1 >> y1 >> x2 >> y2;
        cout << dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1] << endl;
    }

    return 0;
}