相关推荐：堆（Heap） / 堆排序（HeapSort） / TopK

1.树

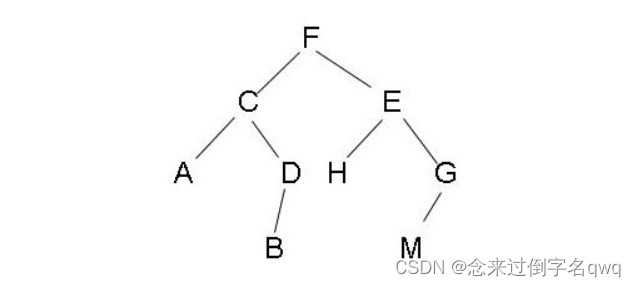
树是一种非线性的数据结构，它看起来像一棵倒挂的树，根朝上而叶子朝下。下图是一棵二叉树，每个节点最多只有两个孩子节点。

1.1 树相关概念

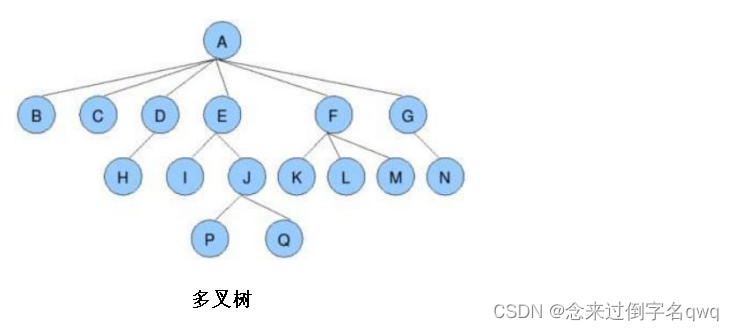
1. 根节点：如上图A节点就是根节点。
2. 节点的度：一个节点含有的子树的个数，如上图A节点的度为6，F节点的度为3。
3. 叶节点：度为0的节点，如上图B、C、H、I…等节点为叶节点。
4. 父节点：也叫双亲节点，如上图E是I和J的父节点，其它节点同理。
5. 子节点：也叫孩子节点，如上图B、C、D、E等是A的孩子节点。
6. 兄弟节点：具有相同父节点的节点，如上图P、Q是兄弟节点。
7. 树的度：最大的节点的度称为树的度，如上图树的度为6。
8. 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推。
9. 树的高度或深度：树中节点的最大层次，如上图树的高度为4。
10. 森林：由m（m>0）棵互不相交的树的集合称为森林。
    

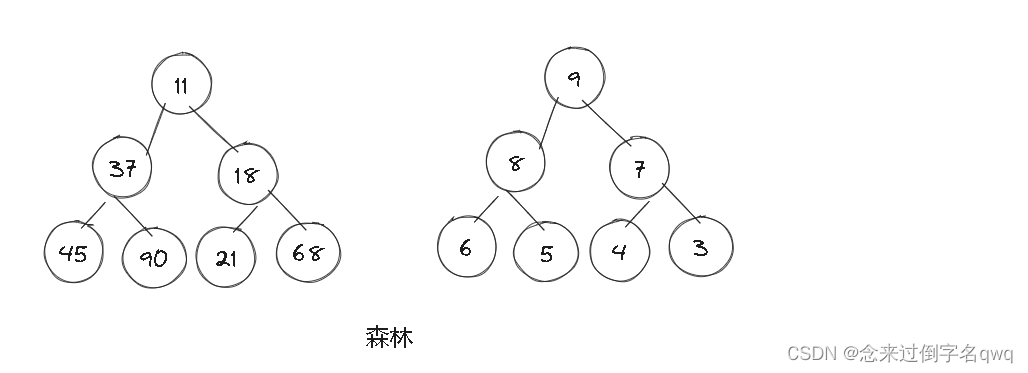
1.2 举例树的应用

Linux的文件系统：

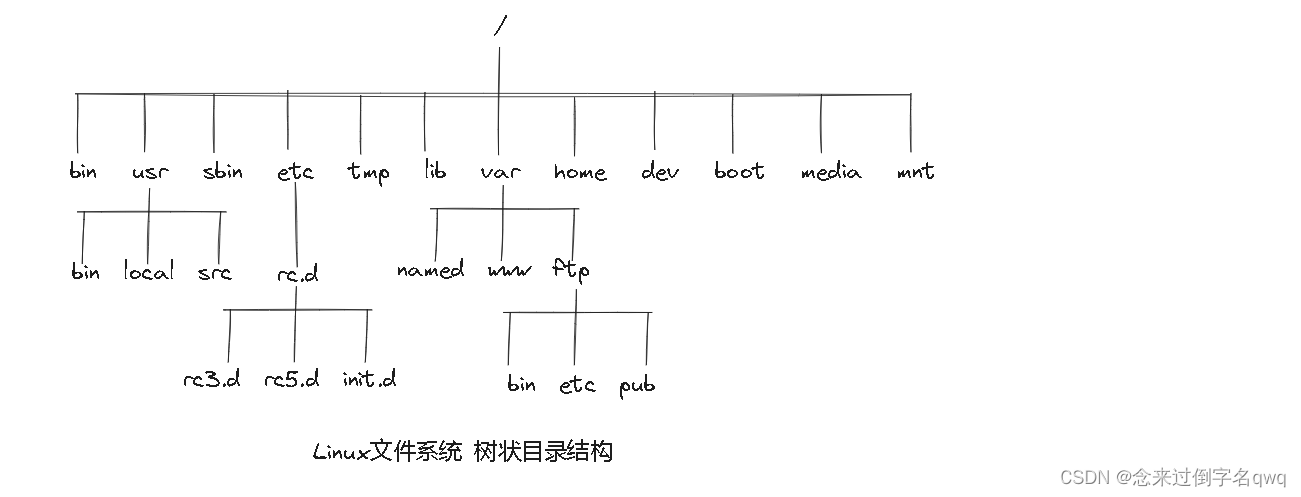
Windows的文件系统也是多叉树，和Linux文件系统不同的是Windows的文件系统可以是森林（至少分了两个盘）。

2. 二叉树

2.1 二叉树分类

普通的二叉树是没有意义的，存储数据并不比链表或数组好，真正让二叉树有意义的是二叉搜索树（又称二叉排序树或二叉查找树）、AVL树（平衡二叉树）、B树和红黑树。

二叉搜索树：简单地说就是左孩子节点比父节点小、右孩子节点比父节点大的树，二叉树的好处是遍历很快，从名字也能得出它是干嘛的。

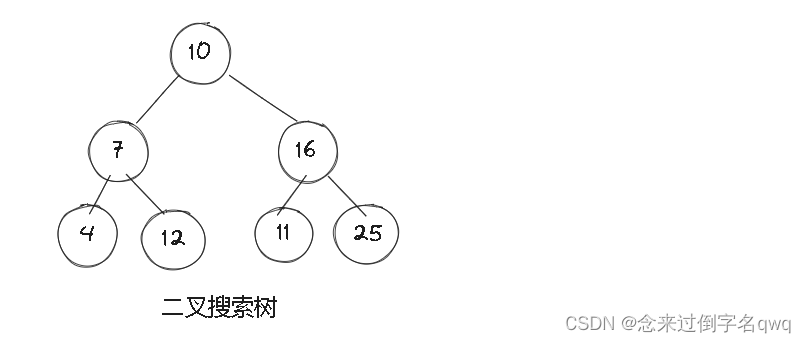
不过极端的二叉搜索树则会造成很多浪费，不仅树另一边节点存储无效的NULL值，最要命的是遍历的时间复杂度增高。

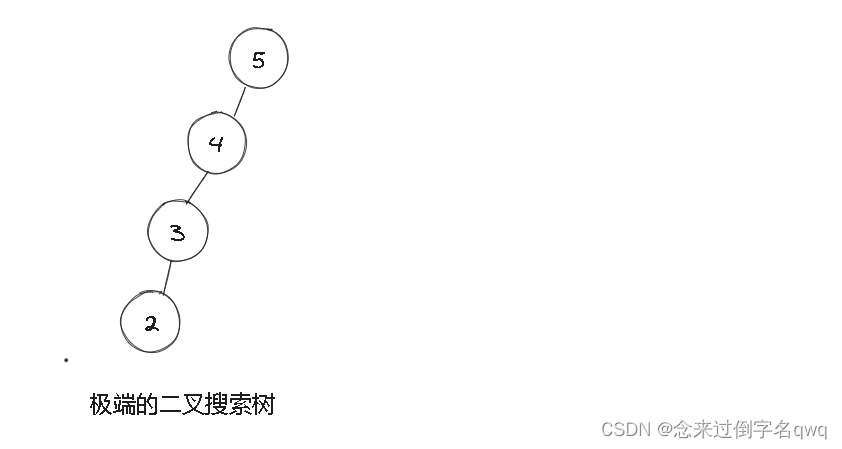
平衡二叉树二叉树可以解决二叉搜索树的缺点，是其升级版，另外还有B树、红黑树等，感兴趣的小伙伴自行了解或看我其它相关文章，否则本篇文章会占用大量篇幅。

2.2 特殊的二叉树

1. 满二叉树：每层的节点都是满的。
2. 完全二叉树：假设树的高度是h，前h-1层的节点都是满的，最后一层也就是h层的节点不一定满，但一定要是有序。满二叉树也是一种特殊的完全二叉树，另外 堆（heap）也是完全二叉树，想了解的可以看这篇文章：堆（Heap）。
   

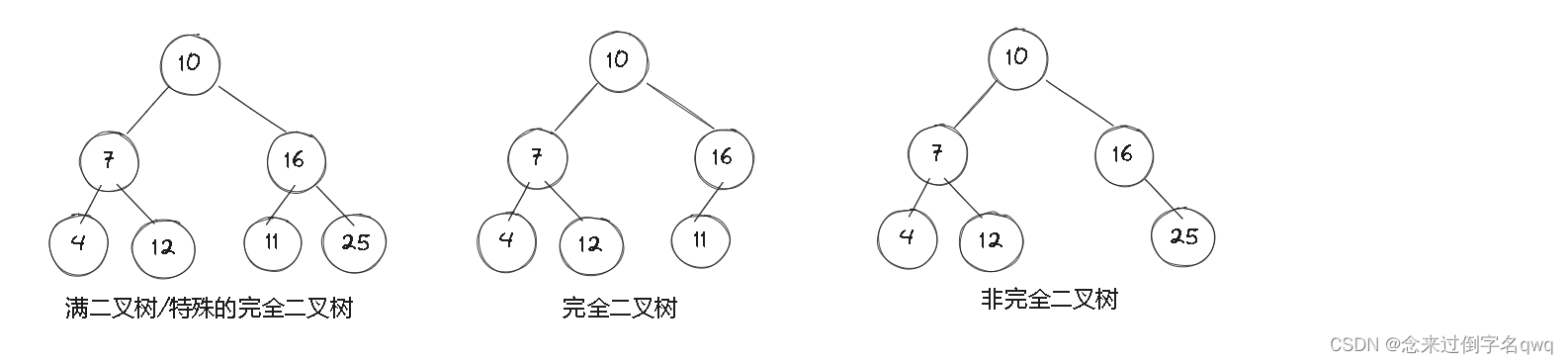
2.3 二叉树的存储结构

二叉树可以使用两种结构存储：顺序结构或链式结构，说白了就是数组或链表。

不过对于二叉树而言基本都是用链表存储，因为用数组存储二叉树会浪费很多空间，而极端的二叉树搜索树更甚。

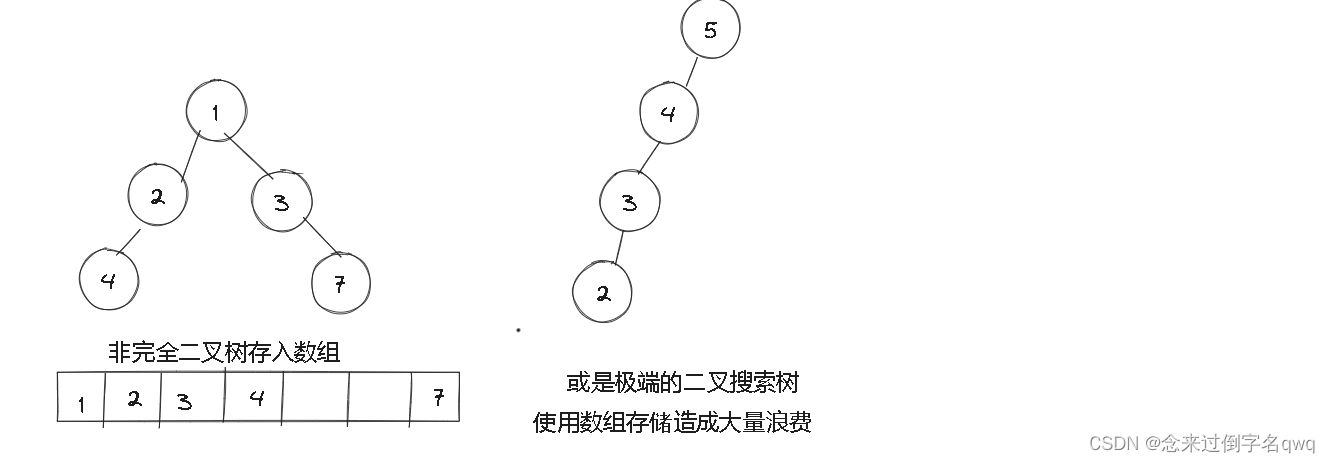
只有完全二叉树/完全二叉树/堆才适合用数组存储，其特性就决定了不会浪费数组空间，为什么非完全二叉树用数组存储会浪费内存空间，而完全二叉树不会，具体了解请看 文章：堆（Heap）。

C语言表示二叉树的结构：

typedef int valtype;
typedef struct TreeNode {
	valtype val;
	struct TreeNode* left;
	struct TreeNode* right;
} TreeNode;

3. 二叉树实现与热门问题

由于普通的二叉树插入删除操作都是没有意义的，所以这里不实现这种操作；另外由于二叉树通常使用链式存储，所以很多操作都是通过递归实现。

申明：

#pragma once

#include <stdio.h>
#include <stdlib.h>

typedef int valtype;
typedef struct TreeNode {
	valtype val;
	struct TreeNode* left;
	struct TreeNode* right;
} TreeNode;

TreeNode* NewNode(valtype val);

// 前、中、后序遍历
void PreOrder(TreeNode* root);
void InOrder(TreeNode* root);
void PostOrder(TreeNode* root);

// 树节点个数
size_t TreeSize(TreeNode* root);
// 叶子节点个数
size_t TreeLeafSize(TreeNode* root);
// 树高度/深度
size_t TreeHeight(TreeNode* root);
// 第k层节点个数
size_t TreeKthSize(TreeNode* root, int k);

实现：

#define _CRT_SECURE_NO_WARNINGS 1

#include "BinaryTree.h"

TreeNode* NewNode(valtype val) {
	TreeNode* treeNode = (TreeNode*)malloc(sizeof(TreeNode));
	if (treeNode == NULL) {
		perror("BuyNode malloc failed.\n");
		exit(-1);
	}
	treeNode->val = val;
	treeNode->left = NULL;
	treeNode->right = NULL;
	return treeNode;
}

void PreOrder(TreeNode* root) {
	if (root != NULL) {
		printf("%d ", root->val);
		PreOrder(root->left);
		PreOrder(root->right);
	}
}

void InOrder(TreeNode* root) {
	if (root != NULL) {
		InOrder(root->left);
		printf("%d ", root->val);
		InOrder(root->right);
	}
}

void PostOrder(TreeNode* root) {
	if (root != NULL) {
		PostOrder(root->left);
		PostOrder(root->right);
		printf("%d ", root->val);
	}
}

size_t TreeSize(TreeNode* root) {
	return root == NULL // 本身 + 左子树 + 右子树节点之和
		? 0 : 1 + TreeSize(root->left) + TreeSize(root->right);
}

size_t TreeLeafSize(TreeNode* root) {
	if (root == NULL) {
		return 0;
	}
	// 非叶子结点的左子树和右子树的叶子节点之和
	return root->left == NULL && root->right == NULL
		? 1 : TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

size_t TreeHeight(TreeNode* root) {
	if (root == NULL) {
		return 0;
	}
	// 选出左子树和右子树中较高的树 + 根节点本身高度
	return max(TreeHeight(root->left), TreeHeight(root->right)) + 1;

	//size_t left = TreeHeight(root->left);
	//size_t right = TreeHeight(root->right);
	//return (left > right ? left : right) + 1; 
}

size_t TreeKthSize(TreeNode* root, int k) {
	if (root == NULL || k < 1) {
		return 0;
	}
	else if (k == 1) { 
		return 1; // 第k层
	}
	else { // k > 1 向下走直到来到第k层
		return TreeKthSize(root->left, k-1) + TreeKthSize(root->right, k-1);
	}
}

测试：

#define _CRT_SECURE_NO_WARNINGS 1

#include "BinaryTree.h"

static void BuildTree(TreeNode* root);

int main() {
	TreeNode root; 
	BuildTree(&root);

	PreOrder(&root);
	printf("\n");
	InOrder(&root);
	printf("\n");
	PostOrder(&root);
	printf("\n");

	printf("TreeSize = %zd\n", TreeSize(&root));
	printf("TreeLeafSize = %zd\n", TreeLeafSize(&root));
	printf("TreeHeight = %zd\n", TreeHeight(&root));
	printf("TreeKthSize = %zd\n", TreeKthSize(&root, 3));
	return 0;
}

static void BuildTree(TreeNode* root) {
	TreeNode* node2 = NewNode(2);
	TreeNode* node3 = NewNode(3);
	TreeNode* node4 = NewNode(4);
	TreeNode* node5 = NewNode(5);
	TreeNode* node6 = NewNode(6);
	TreeNode* node7 = NewNode(7);
	root->val = 1;
	root->left = node2;
	root->right = node4;
	node2->left = node3;
	node2->right = node7;
	node4->left = node5;
	node4->right = node6;
}