难度参考
难度:中等
分类:数组
难度与分类由我所参与的培训课程提供,但需要注意的是,难度与分类仅供参考。且所在课程未提供测试平台,故实现代码主要为自行测试的那种,以下内容均为个人笔记,旨在督促自己认真学习。
题目
给定一个包含n个整数的数组nums和一个目标值target,判断nums中是否存在四个元素a,b,c和d,使得a+b+c+d的值与target相等?找出所有满足条件且不重复的四元组。
示例1:
输入:nums=[1,0,-1,0,-2,2]和target=0
输出:[[-1,0,0,1],[-2,-1,1,2],[-2,0,0,2]]
额外要求:
·答案中不可以包含重复的四元组
思路
-
排序: 首先将数组
nums排序。排序是为了后面能够方便地跳过重复的元素。 -
循环遍历: 使用两层嵌套循环遍历数组,外层循环选择第一个数字
a,内层循环选择第二个数字b。 -
双指针寻找: 内层循环固定了
a和b之后,使用一对双指针left和right(分别初始化为b之后的下一个元素和数组末尾的元素)来查找剩下的两个数字。 -
移动双指针: 如果
a + b + nums[left] + nums[right]的和小于target,则移动left指针;如果和大于target,则移动right指针;如果和等于target,则将这四个元素作为一组加入结果集。 -
跳过重复元素: 在循环和双指针移动的过程中,每当我们要移动某个指针时,如果下一个数字与当前数字相同,那么我们就继续移动指针,直到遇到一个不同的数字为止。这样可以避免重复的组合加入结果集。
-
返回结果: 最后返回存放所有四元组的结果集。
示例
假设我们得到的输入是nums = [1, 0, -1, 0, -2, 2],并且target = 0。
-
排序:
排序后的nums数组将是[-2, -1, 0, 0, 1, 2]。 -
循环遍历与双指针寻找:
a. 在最外层循环中,我们首先选择
-2作为a。此时i=0。b. 在第二层循环中,我们选择
-1作为b。此时j=1。c. 现在我们将
left设为j+1,即2的位置,right设为数组的最后一个元素的位置,即2的位置。d. 进行双指针查找,我们开始检查
sum = a + b + nums[left] + nums[right]是否等于target。 -
移动双指针:
a. 第一次计算得到
sum = -2 + (-1) + 0 + 2 = -1,这比target小,所以我们移动左指针left向右一位。b. 现在left在第三个0的位置上,我们再次计算得到
sum = -2 + (-1) + 0 + 2 = -1,依然比target小,所以我们再次移动左指针。c. 左指针不断右移,直到
left和right指向同一个元素或者left在right左边时停止。 -
找到合适的组合:
a. 如果在移动指针的过程中找到
sum = target,例如我们发现nums[0] + nums[1] + nums[3] + nums[5] = -2 + (-1) + 0 + 2 = 0,我们加入这个组合[-2, -1, 0, 2]到结果集中。 -
跳过重复元素:
如果有重复的元素,例如在
nums = [1, 0, -1, 0, -2, 2]排序后的数组中从第三个元素开始到第四个元素是0,我们在寻找组合[-1, 0, 0, 1]之后,需要跳过所有接下来的相同的数字(这里是0),以避免重复的组合被加入结果集。
梳理
这种解法有效地解决了四数之和的问题,它使用了以下几个关键的处理方式:
-
排序: 这是双指针方法能够工作的前提。通过对原数组进行排序,我们能够以线性的方式(通过移动指针)来改变所选元素组合的和(sum)。如果和小了,我们可以通过移动左指针向右方向增大;如果和大了,可以通过移动右指针向左方向减小。
-
双指针寻找: 这是减少算法复杂度的关键。对于已排序的数组,固定两个数后,可以在
O(n)的时间内通过双指针找到符合条件的其他两个数,该策略避免了简单粗暴的四层循环(O(n^4))。 -
跳过重复元素: 这种处理方式利用了数组已排序的性质。当固定住一个或多个数字时,为了避免重复出现解,需要跳过数组中接下来的相同数字。这种去重是通过在循环和双指针移动的过程中检测相邻数字是否相同来实现的。
这个解法借鉴了三数之和问题(3Sum)的经典解法,扩展到了四个数字,使得该问题的时间复杂度从O(n^4)降低到了O(n^3)。它有效地运用了双指针技巧来减少对时间复杂度的需求,同时也利用了排序以及跳过重复元素来确保找到所有可能的唯一结果。这种方法在解决类似的求和问题中是相当常见和高效的。
三数之和:算法练习-三数之和(思路+流程图+代码)-CSDN博客

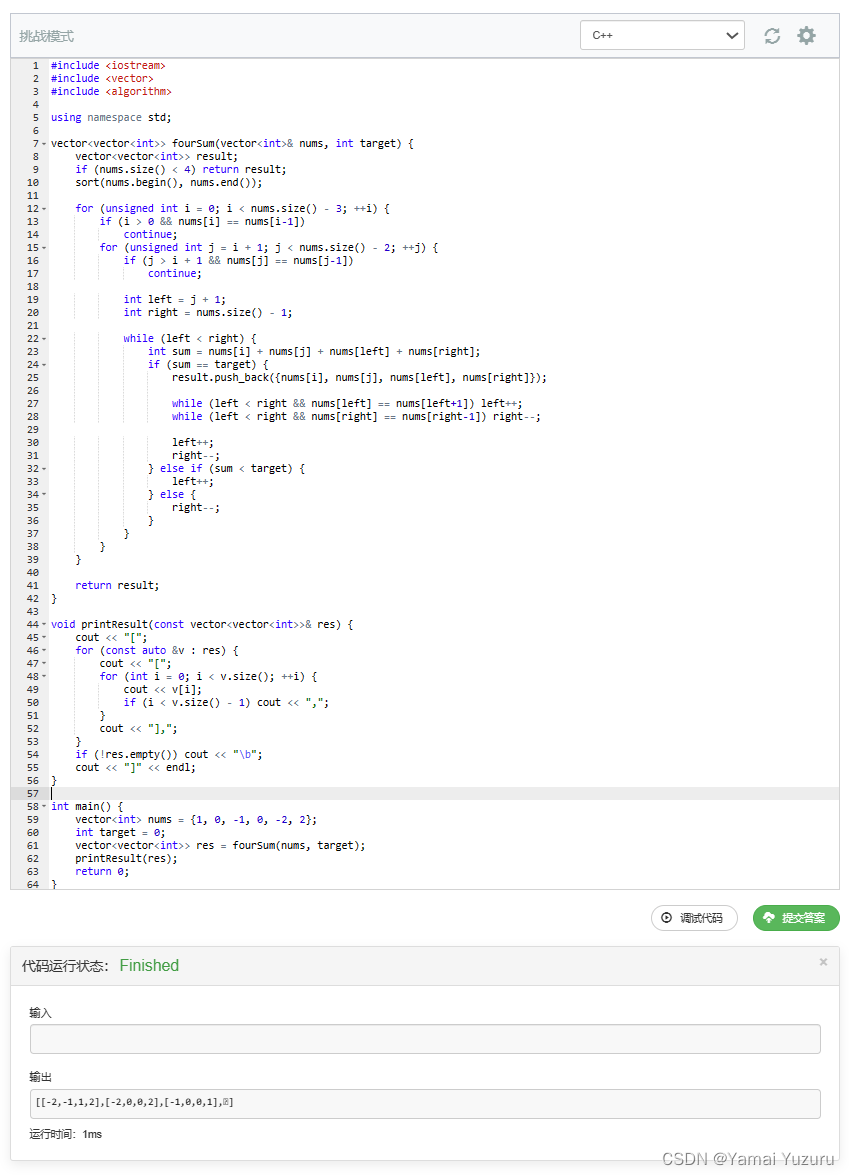
代码
#include <iostream> // 导入输入输出流的库
#include <vector> // 导入向量容器的库
#include <algorithm> // 导入算法库(包括sort)
using namespace std; // 使用标准命名空间以简化代码
// fourSum函数,找出所有和为target的四元组合
vector<vector<int>> fourSum(vector<int>& nums, int target) {
// 初始化返回的结果集
vector<vector<int>> result;
// 当输入向量的大小小于4时,不可能有四个数的组合,直接返回空的结果集
if (nums.size() < 4) return result;
// 对输入向量进行排序,为了后续操作可以采用双指针的方法
sort(nums.begin(), nums.end());
// 第一层循环,确定第一个数
for (unsigned int i = 0; i < nums.size() - 3; ++i) {
// 如果当前数字和之前的数字相同,则跳过,以避免产生重复结果
if (i > 0 && nums[i] == nums[i-1])
continue;
// 第二层循环,确定第二个数
for (unsigned int j = i + 1; j < nums.size() - 2; ++j) {
// 如果当前数字和之前的数字相同,则跳过,以避免产生重复结果
if (j > i + 1 && nums[j] == nums[j-1])
continue;
// 第三层循环采用双指针方法,确定剩下的两个数
int left = j + 1; // 左指针初始化
int right = nums.size() - 1; // 右指针初始化
// 使用双指针在剩余数组中寻找合适的两个数字,使得这四个数字之和为target
while (left < right) {
// 计算当前四个数的和
int sum = nums[i] + nums[j] + nums[left] + nums[right];
// 如果四数之和等于目标和,则将它们作为一个四元组添加到结果集中
if (sum == target) {
// 添加到结果集
result.push_back({nums[i], nums[j], nums[left], nums[right]});
// 为了避免添加重复的四元组,需要将左指针移到下一个不同的数
while (left < right && nums[left] == nums[left+1]) left++;
// 同样的,将右指针移到上一个不同的数
while (left < right && nums[right] == nums[right-1]) right--;
// 将左、右指针各自移到下一个位置
left++;
right--;
// 如果四数之和小于目标和,则将左指针右移,增加总和
} else if (sum < target) {
left++;
// 如果四数之和大于目标和,则将右指针左移,减少总和
} else {
right--;
}
}
}
}
// 返回最终结果集
return result;
}
// 辅助函数,用于打印四数之和的结果
void printResult(const vector<vector<int>>& res) {
cout << "["; // 开始打印输出结果
// 遍历所有的四元组并打印它们
for (const auto &v : res) {
cout << "[";
for (int i = 0; i < v.size(); ++i) {
cout << v[i];
if (i < v.size() - 1) cout << ","; // 用逗号分隔同一个四元组的数
}
cout << "],"; // 结束四元组的打印
}
if (!res.empty()) cout << "\b"; // 如果结果集不为空,则去掉最后一个多余的逗号
cout << "]" << endl; // 结束打印输出结果
}
int main() {
// 创建一个示例向量
vector<int> nums = {1, 0, -1, 0, -2, 2};
// 定义目标和
int target = 0;
// 调用函数并保存结果
vector<vector<int>> res = fourSum(nums, target);
// 打印结果
printResult(res);
// main函数正常退出
return 0;
}打卡