目录
求和
0求和 - 蓝桥云课 (lanqiao.cn)
可获得的最小取值
0可获得的最小取值 - 蓝桥云课 (lanqiao.cn)
领地选择
P2004 领地选择 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
求和
0求和 - 蓝桥云课 (lanqiao.cn)
思路:先对公式进行合并同类相,然后用前缀和
完整代码:
#include <bits/stdc++.h>
#define int long long
const int N = 2e6 + 10;
int a[N], sum[N];
int ans;
signed main() {
int n;
std::cin >> n;
for (int i = 1; i <= n; i++) {
std::cin >> a[i];
sum[i] = a[i] + sum[i - 1];
}
for (int i = 1; i <= n; i++) {
ans += a[i] * (sum[n] - sum[i]);
}
std::cout << ans;
return 0;
}可获得的最小取值
0可获得的最小取值 - 蓝桥云课 (lanqiao.cn)
思路:
第一个情况是取数组前面两个数,第二个情况是取数组末尾的一个元素,如果循环k次一一比较的话,那么{1,1,1,1,1,1,3},若k=3,最小值就是6,这个是贪心的思想,可是最小值应该是5(3+1+1)。
如果第一个情况做 p 次的话,第二个情况就做 k-p 次
此时的总和为
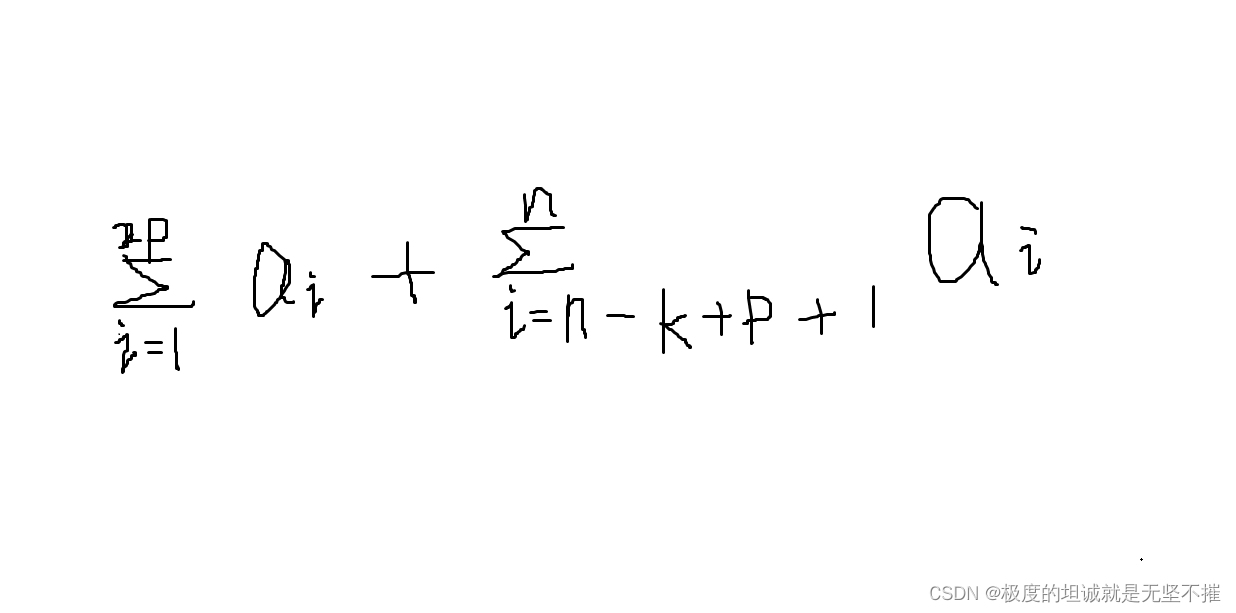 所以遍历一遍p的值
所以遍历一遍p的值
完整代码:
#include <bits/stdc++.h>
#define int long long
const int N = 2e5+10;
int a[N],s[N];
signed main()
{
int n,k;
std::cin >> n >> k;
for(int i = 1;i <= n;i ++)
{
std::cin >> a[i];
}
std::sort(a+1,a+1+n);
// for(int i = 1;i <= n;i ++)
// {
// std::cout<<a[i]<<" ";
// }
// std::cout<<"\n";
for(int i = 1;i <= n;i ++)
{
s[i]=s[i-1]+a[i];
}
// for(int i = 1;i <= n;i ++)
// {
// std::cout<<s[i]<<" ";
// }
// std::cout<<"\n";
int ans=1e18;
for(int i = 1;i <= k;i ++)
{
ans=std::min(ans,s[n]-s[n-(k-i)]+s[2*i]);
}
std::cout<<ans;
return 0;
}领地选择
P2004 领地选择 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路:
这道题用暴力会超时,先用一个数组记录二维前缀和,再来遍历
二位前缀和
从原点开始:s[i,j]=s[i,j-1]+s[i-1,j]-s[i-1,j-1]+a[i,j]
(x1,y1),(x2,y2)中的所有数之和为
s[x2,y2]+s[x1-1,y1-1]-s[x1-1,y2]-s[x2,y1-1]
完整代码:
#include <bits/stdc++.h>
#define int long long
const int N = 1e3+10;
int a[N][N];
int sum[N][N];
signed main()
{
int n,m,c;
std::cin >> n >> m >> c;
for(int i = 1;i <= n;i ++)
{
for(int j = 1;j <= m;j ++)
{
std::cin >> a[i][j];
sum[i][j]=a[i][j]+sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1];
}
}
int maxx=-1e18,maxy=-1e18,ans=-1e18;
for(int i = 1;i <= n-c+1;i ++)
{
for(int j = 1;j <= m-c+1;j ++)
{
int x1=i,y1=j,x2=i+c-1,y2=j+c-1;
int num=sum[x2][y2]+sum[x1-1][y1-1]-sum[x1-1][y2]-sum[x2][y1-1];
if(num>ans)
{
ans=num;
maxx=x1;
maxy=y1;
}
}
}
std::cout<<maxx<<" "<<maxy;
return 0;
}




![[ECE] P2.3Determine t_P_LH and t_P_HL from the oscilloscope](https://img-blog.csdnimg.cn/direct/2d6c748baac941818c67c7447ac9a300.png)