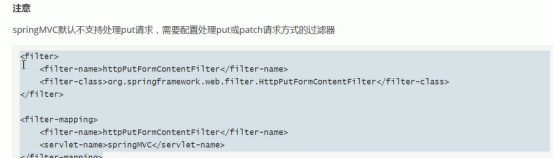
题目

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
在这里插入图片描述

动态规划

参考链接：动态规划详解

简单来说，动态规划其实就是，给定一个问题，我们把它拆成一个个子问题，直到子问题可以直接解决。然后，把子问题答案保存起来，以减少重复计算。再根据子问题答案反推，得出原问题解的一种方法。

一般这些子问题很相似，可以通过函数关系式递推出来。然后，动态规划就致力于解决每个子问题一次，减少重复计算。比如斐波那契数列就可以看做入门级的经典动态规划问题。

核心思想：就在于拆分子问题，记住过往，减少重复计算。

思路

一般看到题目不需要列出来具体的多少种方案，只需要计算有多少种方案，基本上就可以尝试用动态规划算法来解决问题。想好用动态规划就想想动态规划五步曲。

关键词：有多少种方案算法

确定dp数组以及下标的含义：定义dp[i]为爬上第 i 级台阶有多少种方案，爬到第i层楼梯，有dp[i]种方法；
确定状态转移方程：因为每次只可以爬1个或者2个台阶，所以，爬上当前台阶的方案应该是前面两个状态的方案的和，即，dp[i] = dp[i-1] + dp[i-2]。
初始化状态 ：从i = 0 级开始爬的，所以从第 0 级爬到第 0 级，我们可以看作只有一种方案，即 dp[0]=1；i = 1代表从第 0 级到第 1 级，也只有一种方案，即爬1级，dp[1] = 1；i=2代表从第0级到第2级，有两种方案：dp[2]=2。
遍历顺序 ：由状态转移方程可知，dp[i]是从dp[i−1]和 dp[i−2]转移过来，所以从1往100遍历。
返回值 ：一共计算 n 阶楼梯有多少方案，所以返回dp[n]。

斐波那契数列：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）
用递归来做：f(x)=f(x-1)+f(x-2)
爬第1级台阶：1种方法 1 => f(1)=1
爬第2级台阶：2种方法 1+1 ； 2 => f(2)=2
爬第3级台阶：3种方法 1+1+1；1+2；2+1 => f(3)=3
爬第4级台阶：5种方法 1+1+1+1；1+2+1；1+1+2；2+1+1；2+2 => f(4)=5
……
爬第n级台阶：是第n-1级台阶的方案和+第n-2级台阶的方案和 => f(n)=f(n-1)+f(n-2)

# 暴力递归
class Solution(object):
    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """
        dp=[0 for i in range(46)] #  初始化数组为[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
        dp[1]=1
        dp[2]=2
        if (n<=1):return n 
        
        for i in range(3,n+1):
            dp[i]=dp[i-1]+dp[i-2]

        return dp[n]

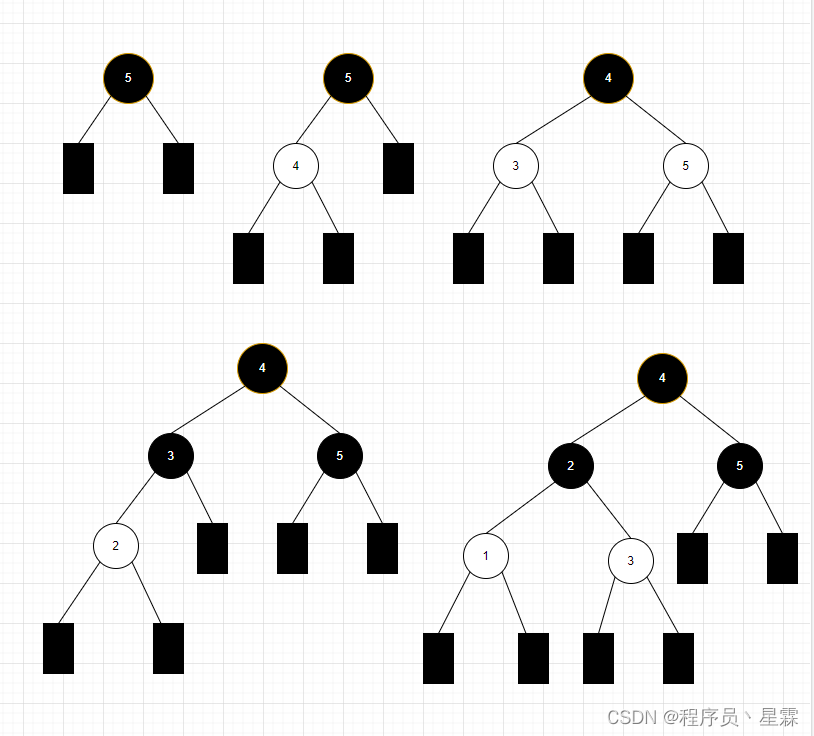
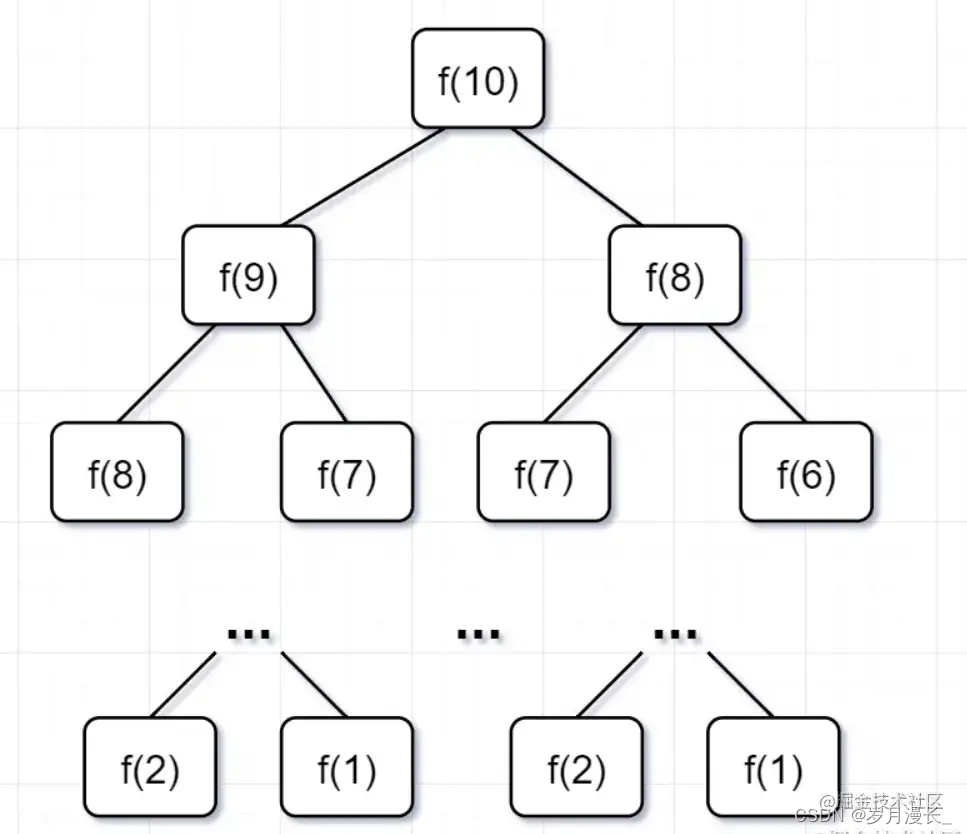
递归树如下：
在这里插入图片描述

递归时间复杂度 = 解决一个子问题时间 * 子问题个数

一个子问题时间 = f（n-1）+f（n-2），也就是一个加法的操作，所以时间复杂度是 O(1)；
问题个数 = 递归树节点的总数，递归树的总节点是 $2^n-1$ ，所以时间复杂度是 $O(2^n)$ 。

所以，递归解法的时间复杂度： $O(1) * O(2^n) = O(2^n)$ ，指数级别的爆炸增长，如果n比较大的话，容易超时。

仔细观察这颗递归树，会发现存在大量重复计算，比如f(8)被计算了两次，f(7)被重复计算了3次…所以这个递归算法低效的原因，就是存在大量的重复计算！

既然存在大量重复计算，那么我们可以先把计算好的答案存下来，即造一个备忘录，等到下次需要的话，先去备忘录查一下，如果有，就直接取就好了，备忘录没有才开始计算，就可以省去重新重复计算的耗时啦！这就是带备忘录的解法。

带备忘录的递归解法（自顶向下）

一般使用一个数组或者一个哈希map充当这个备忘录。保存f(9)~f(1)

其实，还可以用动态规划解决这道题。

自底向上的动态规划

动态规划跟带备忘录的递归解法基本思想是一致的，都是减少重复计算，时间复杂度也都是差不多。但是呢：

带备忘录的递归，是从f(10)往f(1)方向延伸求解的，所以也称为自顶向下的解法。
动态规划从较小问题的解，由交叠性质，逐步决策出较大问题的解，它是从f(1)往f(10)方向，往上推求解，所以称为自底向上的解法。

动态规划有几个典型特征：最优子结构、状态转移方程、边界、重叠子问题。在青蛙跳阶问题中：

f(n-1)和f(n-2) 称为 f(n) 的最优子结构
f(n)= f（n-1）+f（n-2）就称为状态转移方程
f(1) = 1，f(2) = 2就是边界
比如 f(10)= f(9)+f(8), f(9) = f(8) + f(7) ,这里的f(8)就是重叠子问题。

可以发现，f（n）只依赖前面两个数，所以只需要两个变量a和b来存储，就可以满足需求了，因此空间复杂度是O(1)；循环n次，时间复杂度O(n)

我们来看下自底向上的解法，从f(1)往f(10)方向，想想是不是直接一个for循环就可以解决啦，如下：

class Solution(object):
    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """
        p=1  # f(1)
        q=2  # f(2)

        if (n<3):return n 
        else:
            for i in range(3,n+1):
                r = p+q
                p = q
                q = r
            return r

做动态规划的思路：

穷举分析：f(1) ~ f(5)
确定边界：f(1)和f(2)
找出规律，确定最优子结构：
n>=3时，已经呈现出规律 f(n) = f(n-1) + f(n-2) ，因此，f(n-1)和f(n-2) 称为 f(n) 的最优子结构。

什么是最优子结构？
一道动态规划问题，其实就是一个递推问题。假设当前决策结果是f(n)，则最优子结构就是要让 f(n-k) 最优，最优子结构性质就是能让转移到n的状态是最优的，并且与后面的决策没有关系，即让后面的决策安心地使用前面的局部最优解的一种性质
写出状态转移方程：f(n)=f(n-1)+f(n-2)
代码实现：注意从底往上遍历