Python解题 - CSDN周赛第21期

本期比赛都是比较基础的排序、查找，没有多少难度。不过有很多人反映第二题测试数据有问题，基本所有选手在本题上都没得分。最近官方每期比赛都会有类似的数据问题，虽然参赛者对数据有疑问，但从未得到解答，官方也未曾公开数据，而且现在一周双赛，好像所有工作人员都在忙着组织比赛，却没有人根据选手反馈的bug进行解答与修复，给人一种很敷衍、但又着急向上面交差的感觉，希望以后能慢慢改进吧。

第一题：合并序列

有N个单词和字符串T，按字典序输出以字符串T为前缀的所有单词。

示例：

示例
输入
5

oi

od

ki

ko

ka

k

输出
ka

ki

ko

分析

简单的第一题，用python直接判断字符串的前缀是否和给定的 T 相同，然后把结果排序输出即可，因为字符串列表进行排序时默认使用的就是字典序。

参考代码

N = int(input().strip())
arr = [input().strip() for _ in range(N)]
T = input().strip()
result = sorted(i for i in arr if i.startswith(T))
print(*result,sep="\n")

第二题：千问万问

给定大小为 n 的整数序列A。现在会有 q 次询问，询问子区间的整数数量。

分析

本期bug题，按照题目给的思路无法通过测试用例。原题下面还有一段文字描述，记不清了，大致意思就是说这个整数序列是无序的，而且可能存在重复的整数。每次询问会给出左、右边界（ $l$ 和 $r$ ），要求输出该整数序列中位于左右边界内的整数个数。

从示例来看给出的边界是闭区间，也就是要输出整数序列A中满足 $l\leq a\leq r$ 的整数a的数量。

所以，题目理解下来应该不难。但是，用尽所有办法，穷举、遍历、二分，都无法通过哪怕一个用例（示例都能够正常通过），这就不禁让人怀疑题目测试用例是否有问题了。（更新：官方已经承认数据是有问题的）

给一个比较简单的穷举代码吧，进一步解释权留给官方。

参考代码

n, q = map(int, input().strip().split())
nums = list(map(int, input().strip().split()))
for _ in range(q):
    l, r = map(int, input().strip().split())
    res = 0
    for i in nums:
        if l <= i <= r:
            res += 1
    print(res)

第三题：连续子数组的最大和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

分析

连续子数组的最大和，也是经典的基础问题了，而且类似的问题曾在第九期考过，代码都不用改。

时间复杂度为 $O(n)$ 的算法的核心思想是：对序列中每一个整数而言，如果之前的序列之和是负数，就不相加。因为如果加上之前的序列，反而比自己本身的值还要小，而我们要找的是最大值，显然不符合，所以这样的话最大子序列就应该从自己开始算起。

所以，额外定义两个变量，一个用来记录连续相加的子序列之和，一个用来记录最大的子序列之和。使用 max() 函数即可完成比较。当for循环遍历完一遍列表，即可得到结果。

参考代码

n = int(input().strip())
arr = list(map(int, input().strip().split()))
result = temp = arr[0]
for i in arr[1:]:
    temp = max(i, i+temp)
    result = max(result, temp)
print(result)

第四题：降水量

给定n个柱面的高度，表示降雨某地n块区域的海拔高度。计算降雨之后该地最大储水面积。如果低于地平线，也就是小于 0，则一定积水。

示例：

示例一示例二
输入
7

3 4 0 -1 5 2 3

3

-2 -1 -2

输出
10
5

分析

本期稍微有点意思的题目，以前在每日一练也出现过。第一个示例记不清了，我自己编的，但原理都是一样的。

本题类似力扣原题接雨水，所以本期的标题也用了这个名字。题目大意就是说降水后，由于地表高度不同，造成积水，然后问积水的体积——注意，虽然题目里说是面积，但其实参考示例就会发现这里其实是指体积，也许因为只有一个维度，高度，所以体积也变成面积了。

以示例一为例，地形大概就是如下所示：

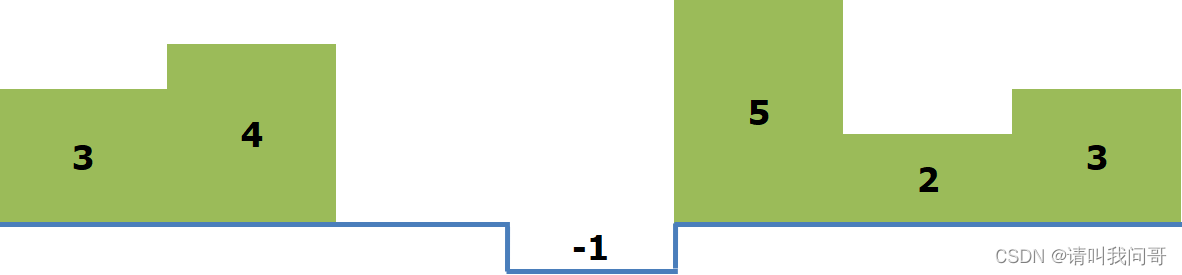
很显然，降水后，两边的水会流失，最后留下的积水如下图（蓝色）所示：

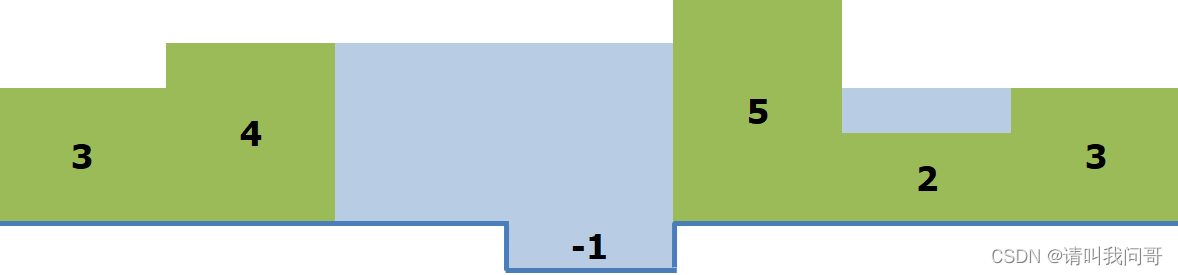
然后我们数一下积水的体积（面积，或格子数量），就可以得到蓝色部分的格子数量是10，也就是最后的答案。

解题的关键在于如何找到这些能够储水的“水坑”，然后将它们的体积加在一起。力扣上也提供了很多题解，问哥这里使用的是模拟的方法（好像没找到和我类似的思路？），模拟“降水”，然后减去左右两边流走的降水，剩下的就是积水了。

具体做法是，先用“降水”填满整个区域数组，也就是找出原数组的最大值 M（本例中是5），然后以最大值为参照对其它元素“取反”，得到“降水”的数组，然后将该数组进行加总，得到总的降水量 S。

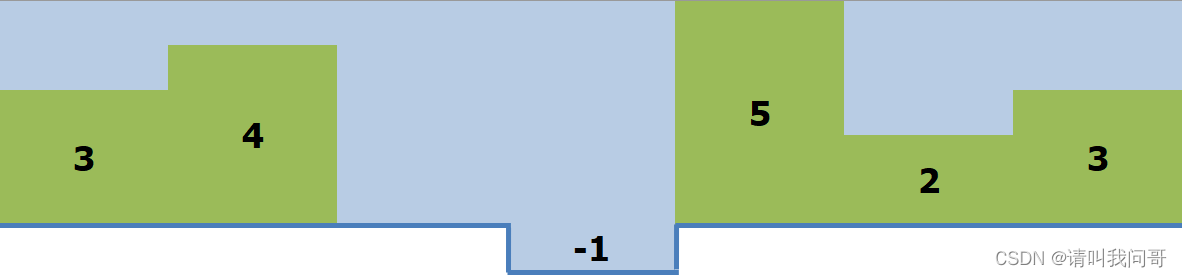
然后从左右两边，依次向中间最高值（降水为0的参照位置）的地方遍历，每遍历一个元素就减去当前“降水”的最小体积，代表流走的降水（下图中灰色的部分），剩下的就是积水的体积了（蓝色部分）。

从图中也可以很容易发现，灰色部分“流走的降水”是两个单调的非递增数组（从左右两边向中间），而这（两）个数组的值是每次遍历降水体积与之前流水相比的较小值（比如从左边遍历到第三个位置，降水是5，但是之前最小的流水是1，所以这个位置也“流走”1单位的降水，从右边遍历到右边第二个位置的时候，这个位置的降水是3，与之前最小的流水2相比，也“流走”2单位的降水）。于是，我们增加一个变量 H，用于保存遍历降水体积时的最小流水体积，每遍历一个位置的降水，就用总降水量 S 减去 H，最终的结果就是剩下的积水体积了。（其实很多类似关于数组的问题都可以这样换个角度解决）

从左右两边向中间参照位置（降水为0）进行两次遍历，总的时间复杂度加在一起还是 $O(n)$ ，但是这里还要考虑到有三种特殊的情况：

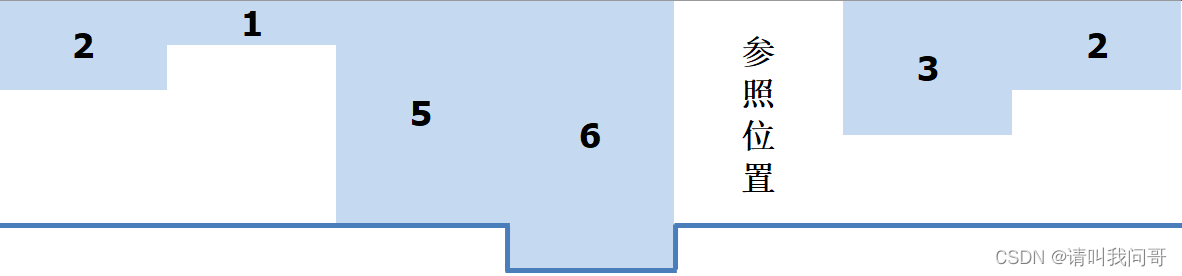
1、有两个以上参照位置。其实这种情况下，思路不用做任何改变，整体所用的时间要更短，因为如果存在两个以上参照位置，说明这两个位置的海拔高度相同，那它们之间的地形无论什么样，降水都会变成积水，所以如果从左右向中间遍历的话，遍历到各自最近的参照位置（0）就可以停止遍历了。如下图所示：

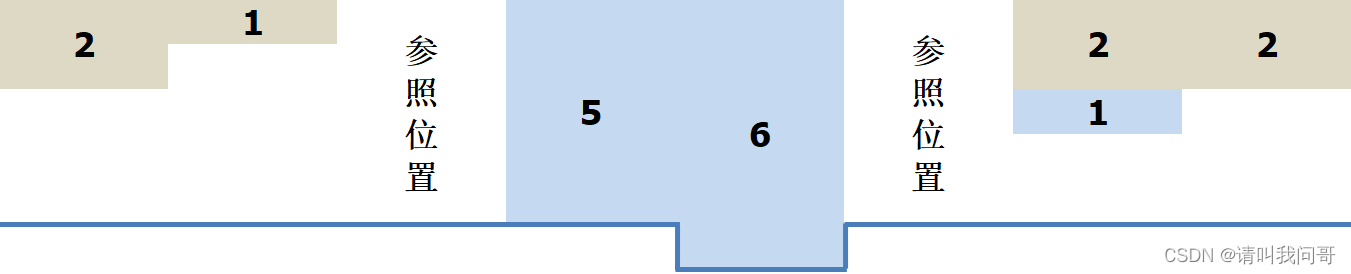
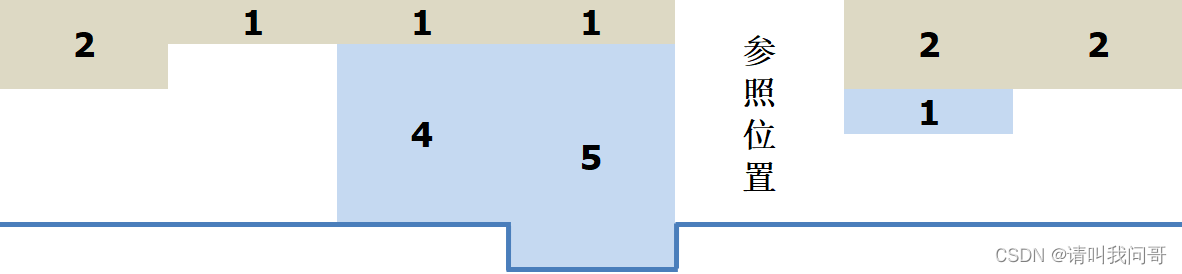
2、左右两边存在水坑（海拔高度为负数，低于地平线）。这种情况下，左右两边的降水并不是全部流走了，水坑里的积水也要统计进去。所以回到我们上面的思路中，用于保存最小流水体积的变量 H 的初始值，应该不大于参照位置的体积 M，比如下图中左右两边最大的降水是6，但是流走的降水体积是5，也就是参照位置的体积。所以在遍历开始时，需要加一个判断，H 的初始值最大不超过 M 。

3、只有水坑，不存在大于0的参照位置，比如示例二。这种情况其实是最简单的，只要把水坑的体积加在一起即可。这样的话需要特判，先要检查区域中是否所有的海拔位置都小于等于0，然后直接返回所有海拔的绝对值的和。但是为了代码的一致性，问哥把这种特判也合并在了上面的思路里。其实只要在一开始选取参照位置的时候，参照位置不小于0即可。只不过这样会需要遍历两遍降水数组（左右向另一边各一遍），然后减去0，最后的答案依然还是总的降水量。由于我们计算时间复杂度的时候只考虑最高项的幂，所以时间复杂度依然还是 $O(n)$ ，当然，如果对这种情况加入特判的话会更快一些，但代码将会更加冗长。

上述思路的参考实现代码如下：

参考代码

n = int(input().strip())
arr = list(map(int, input().strip().split()))
M = max(0, max(arr))
res = [M-i for i in arr]
S = sum(res)
H = min(M, res[0])
for i in range(n):
    if res[i] == 0: break
    H = min(H, res[i])
    S -= H
H = min(M, res[-1])
for i in range(n-1,-1,-1):
    if res[i] == 0: break
    H = min(H, res[i])
    S -= H
print(S)