十大排序算法之归并排序

news2024/11/28 10:31:58

归并排序

归并排序是包含归并思想的排序方法，它是分治法（Divide and Conquer）的一个典型应用。所谓分治，即将问题“分”（Divide）为更小的问题进行递归求解，再将得到的各个递归结果合并在一起，达到“治”（Conquer）问题的目的，也称“分而治之”。
“分”的阶段可一分为二、一分为三⋯⋯，据此我们也将归并排序分为二路归并、三路归并⋯，此处以二路归并为例进行讲解。

1. 算法思想

先将原数组均分为子序列，一生二，二生四，四生无穷，然后使每个子序列有序，再将两个有序子序列合并为一个有序序列，直到无穷合四，四合二，二合一。

2. 算法步骤

（1）将待排序数组一分为二，再将两个子序列一分为二，成为两个新的待排序数组。
（2）重复步骤（1），直到待排序数组的长度为1。
（3）按原路径将长度为1的两个数组合成一个有序序列，然后一直向前合并，最终就会得到一个完整的有序序列。
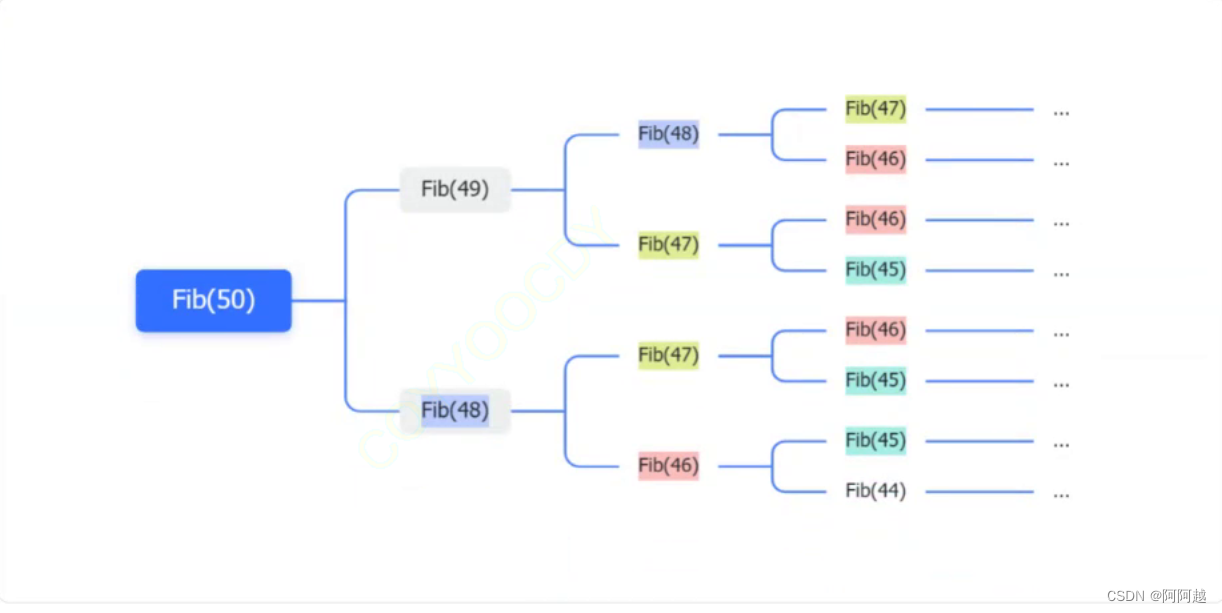
归并排序算法的排序步骤如下图所示。
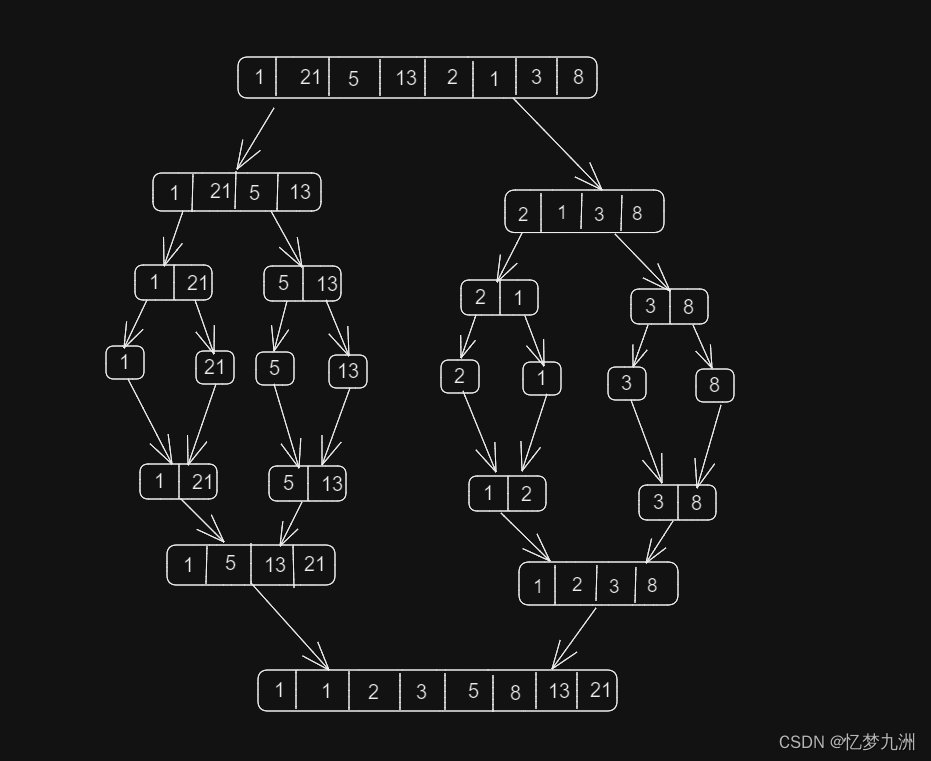
在这里插入图片描述

注意：“分”阶段的结构和完全二又树一模一样，这意味着我们可以使用递归和选代，递归深度为 $log_2n$ 。

3. 算法分析

归并排序是一种十分高效的算法，毕竟能利用完全二叉树特性的算法其性能都不会差。从上图中可以看出，分和合的二又树深度均为 $log_2n$ ，而每次分分合合的平均时间复杂度为O(n)，二者相乘即为总的平均时间复杂度 O(nlog n)，最好和最坏的情况都是一样的。
需要说明的是，归并排序属于稳定排序算法。

4. 算法代码

算法代码如下：
Python

# -*- coding: utf-8 -*-

# 归并排序
def merge (left, right) :
    """
    两个有序子序列的有序合并：
    依次对两个有序列表的最小数进行比较，较小的放入 result中;
    :param left: 左子序列
    :param right: 右子序列
    :return: 左右子序列所合成的有序序列
    """
    # result：存放已经排好顺序的数组
    result=[]
    #如果不符合左右子序列长度均大于0，则说明至少其中的一个数组已无数据
    while len(left) > 0 and len(right)>0:
        # 相等的时候优先把左侧的数放进结果列表，以保证其稳定性
        if left[0] <= right[0]:
            # list.pop （0）为移除并返回列表的第一个元素
            result.append (left.pop (0) )
        else:
            result.append(right.pop(0))
    # 跳出 while 循环后，我们便可以把另一个数组尽数加入 result 后面
    result += left
    result += right
    return result
def merge_sort(array) :
    '''
    无序序列的不断拆分：
    每次均由中间位置进行拆分，不断自我递归调用，直到子序列长度为1
    '''

    # 如果拆分后仅有单个元素，则返回该元素而不再拆分
    if len(array)== 1:
        return array
    #如果有两个及以上元素，则取中间位置进行拆分
    middle = len(array)// 2
    # 拆分后的左侧子串
    array_left = array[:middle]
    #拆分后的右侧子串
    array_right = array[middle:]
    # 对拆分后的左右子序列进行再拆分，直到 len（array） 1
    left = merge_sort(array_left)
    right = merge_sort(array_right)
    # 合并已拆分的左右子序列的同时进行排序并返回排序后的结果
    return merge(left, right)
#调用 merge_sort 函数
print(merge_sort([34,21,13,2,5,1,55,3,1,8]))

Java

  // 合并两个有序子数组的方法
    public static List<Integer> merge(List<Integer> left, List<Integer> right) {
        List<Integer> result = new ArrayList<>();

        while (!left.isEmpty() && !right.isEmpty()) {
            if (left.get(0) <= right.get(0)) {
                result.add(left.remove(0));
            } else {
                result.add(right.remove(0));
            }
        }

        // 将剩余元素全部添加到结果列表中
        while (!left.isEmpty()) {
            result.add(left.remove(0));
        }
        while (!right.isEmpty()) {
            result.add(right.remove(0));
        }

        return result;
    }

    // 归并排序主方法
    public static List<Integer> mergeSort(List<Integer> array) {
        if (array.size() == 1) {
            return array;
        }

        int middle = array.size() / 2;
        List<Integer> arrayLeft = new ArrayList<>(array.subList(0, middle));
        List<Integer> arrayRight = new ArrayList<>(array.subList(middle, array.size()));

        arrayLeft = mergeSort(arrayLeft);
        arrayRight = mergeSort(arrayRight);

        return merge(arrayLeft, arrayRight);
    }
        @Test
        void contextLoads () {
            List<Integer> array = Arrays.asList(34, 21, 13, 2, 5, 1, 55, 3, 1, 8);
            List<Integer> sortedArray = mergeSort(new ArrayList<>(array));
            System.out.println(sortedArray);
        }