前言

合成孔径雷达(Synthetic Aperture Rader, SAR)感觉就是一个小众的领域，尽管笔者的主要研究方向不是这个，但是选修了这门课，在查找资料的过程中发现论文很多，但开源代码非常少，为了方便后来者的学习，将课本中著名的三种成像算法——距离多普勒算法(Range-Doppler, RD)、CS算法(Chirp Scaling, CS)和ωk算法通过MATLAB进行了复现，对课本附录雷达回波数据进行了成像与对比。当然，由于笔者学识有限，不知道代码的具体细节是否有问题，文章与代码有任何问题都可以在评论区或私信交流。
本文代码已开源，所使用的雷达回波数据和算法概念来源于课本《合成孔径雷达成像算法与实现》¹及其附录光盘。

SAR基本概念

雷达获取数据的几何关系

雷达位置波束在地面覆盖区的简单几何模型及相关概念如下图所示。

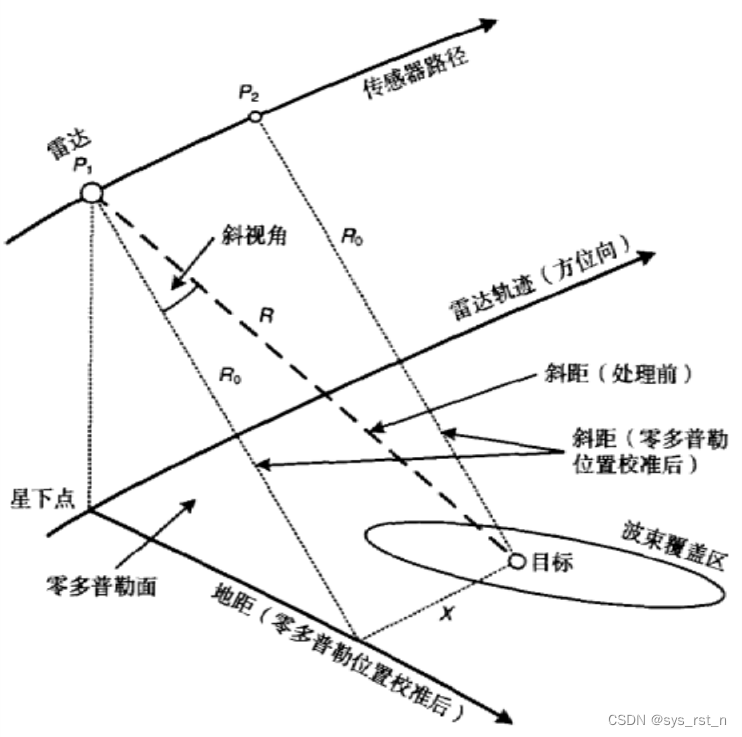
低斜视角下的回波信号模型

基于上述简单几何模型，由于书本附录的雷达回波数据由RADARSAT产生，这是一款小斜视角和中等孔径长度的传感器，因此基带接收信号可近似为：
s 0 ( τ , η ) ≈ A 0   ω r ( τ − 2 R ( η ) c )   ω a ( η − η c )   e x p { − j 4 π R 0 λ }   ∗   e x p { − j π K a η 2 }   e x p { j π K r [ τ − 2 R ( η ) c ] 2 } s_0(\tau, \eta)\approx A_0 \,\omega_r(\tau-\frac{2R(\eta)}{c}) \, \omega_a(\eta-\eta_c) \, \mathrm {exp}\{-j\frac{4\pi R_0}{\lambda}\}\\ \, \\ \ast \, \mathrm{exp}\{-j\pi K_a \eta^2\}\, \mathrm{exp}\{j\pi K_r[\tau - \frac{2R(\eta)}{c}]^2\} s0​(τ,η)≈A0​ωr​(τ−c2R(η)​)ωa​(η−ηc​)exp{−jλ4πR0​​}∗exp{−jπKa​η2}exp{jπKr​[τ−c2R(η)​]2}
其中，$\tau$为距离向时间（快时间）；$\eta$为方位向时间（慢时间）；$A_0$为目标后向散射系数的幅度；${\omega }_r$为传输雷达脉冲包络；${\omega }_a$为方位向天线波束方向图；$R_0$为最近点斜距；$\lambda$为发射脉冲中心频率对应的波长；$c$为光速；$K_r$为传输信号的调频率，即距离向调频率；$K_a$为方位向调频率，计算方式如：
$$K_a\approx \frac{2V_r^2{f}_0}{c{R}_0}$$
其中，$V_r$为雷达等效速度。$R(\eta )$为距离方程，对双曲线距离等式进行抛物线近似有：
$$R(\eta )=\sqrt{R_0^2+V_r^2{\eta }^2}\approx R_0+\frac{V_r^2{\eta }^2}{2R_0}$$

RADARSAT-1主要参数

课本附录的回波数据使用RADARSAT-1雷达采集，根据附录可以得到成像所需的参数如下表：

参数	符号	值	单位
距离向采样率	$F_r$	32.317	MHz
方位向采样率	$F_a$	1257	Hz
脉冲中心频率	$f_0$	5.3	GHz
脉冲持续时间	$T_r$	0.4175	μs
最近点斜距	$R_0$	988.65	km
距离向调频率	$K_r$	-0.72135	MHz/μs
光速	c	299790	km/s
等效雷达速度	$V_r$	7062	m/s
方位向调频率	$K_a$	1733	Hz/s
多普勒中心频率	$f_{nc}$	-6900	Hz

数据预处理

数据读取与再封装

由于课本附录给出的提取方法过于复杂，我将两段回波数据提取出来并进行ACG增益电平校正后，以complex int8（有符号单字节整形复数）的形式分别另存为“CDdata1.mat”和"CDdata2.mat"两个MATLAB工作区存档文件，使用时直接加载即可。在成像中直接对两个回波数据进行拼接可得到完整的区域回波数据。

数据补零

测试发现回波数据成像后，与说明书附录的成像结果参考图对比，发现存在方位向与距离向的二维混叠，且西岸岛屿的位置分布与实际不符，推测回波数据的边缘被压缩了，因此在开始处理前，还做了时域二维补零处理。
补零的思想为，将回波矩阵放在中间，然后往距离向和方位向的两边补等量的零值。补零前回波矩阵的大小为方位向距离向=30722048，多次实验发现补零到4096*3414效果最好。

成像算法

坐标轴的产生

回波数据在内存中的保存方式如下图所示，保存为了一个复数矩阵，该矩阵的行数和列数分别为方位向点数和距离向点数。

三种仿真的成像算法使用一样的坐标轴，基于回波数据矩阵产生。
距离向时间轴$t_r$以距离向采样率$F_r$的倒数为间隔，取值范围为：
$$\frac{2R_0}{c}-\frac{N_r}{2F_r}\le t_r\le \frac{2R_0}{c}+\frac{N_r}{2F_r}$$
其中，$N_r$为回波的距离向点数。距离向频率轴$f_r$以距离向采样率$F_r$除以距离向采样点数$N_r$为间隔，取值范围为：
$$-\frac{F_r}{2}\le t_r\le \frac{F_r}{2}$$
需要注意的是：由于对信号做FFT后0频率数组在两端，最高频率在中间，因此获得频率轴（距离向与方位向都一样）后，需要利用“fftshift”函数将数据两边与中间翻转，使零值在两边，最大值和最小值在中间，如此才能让频率轴与实际频率一一对应。
方位向时间轴$t_a$以方位向采样率$F_a$的倒数为间隔，取值范围为：
$$-\frac{N_a}{2F_a}\le t_a\le \frac{N_a}{2F_a}$$
方位向频率轴$f_a$以方位向采样率$F_a$除以方位向采样点数$N_a$为间隔，取值范围为：
$$f_{nc}-\frac{F_a}{2}\le f_a\le f_{nc}+\frac{F_a}{2}$$
与方位向频率轴一样，利用“fftshift”函数将其零值移动到两边。

RD算法

距离多普勒算法是在1976年至1978年为处理SEASAT SAR数据而提出的SAR成像算法，至今仍在广泛使用，它通过距离和方位上的频域操作达到高效的模块化处理要求。
由于距离徙动校正是在距离时域-方位频域中实现的，而方位向频率等于多普勒频率，所以该处理域也称为“距离多普勒域”。距离徙动校正的的“距离多普勒”域实现正是是RD算法与其它算法的主要区别，因而称其为距离多普勒算法。
本文使用的为基本的RDA，算法流程如下图所示：

RD算法的不足之处在于当用较长的核函数提高距离徙动校正精度时运算量较大；此外，二次距离压缩

距离压缩

利用下式计算距离向匹配滤波器：
$${echo}_{{d1}_{mf}}=\exp \left(\frac{i\pi \ast {f_r}^2}{K_r}\right)$$
对回波信号矩阵$echo$做距离向傅里叶变换后，乘上上述匹配滤波器，然后距离向逆傅里叶变换，得到信号${echo}_{s1}$：
e c h o s 1 = i f f t r { f f t r { e c h o } ∗ e c h o d 1 m f } {echo}_{s1}=\mathrm{ifft_r} \{\mathrm{fft_r}\{echo\}\ast {echo}_{{d1}_{mf}}\} echos1​=ifftr​{fftr​{echo}∗echod1mf​​}

距离徙动矫正

为了防止方位向发生混叠，先令${echo}_{s1}$乘上$\exp \left(-2\pi i{f}_{nc}{t}_a\right)$实现方位向下采样。然后计算徙动校正乘法器G：
$$\begin{array}{rl}D& =\frac{{\lambda }^2\ast R_0\ast {f_a}^2}{8{V_r}^2}\\ & \\ G& =\exp \left(\frac{4\pi i\ast f_r\ast D}{c}\right)\end{array}$$
令下采样后的${echo}_{s1}$做方位向傅里叶变换，然后乘上徙动校正乘法器G得到${echo}_{s2}$：
e c h o s 2 = f f t a { e c h o s 1 } ∗ G {echo}_{s2}=\mathrm{fft_a}\{{echo}_{s1}\}\ast G echos2​=ffta​{echos1​}∗G

方位压缩

计算方位向匹配滤波器${echo}_{{d3}_{mf}}$为：
$${echo}_{{d3}_{mf}}=\exp \left(\frac{-\pi i\ast {f_a}^2}{K_a}\right)$$
令${echo}_{s2}$乘上上述方位向匹配滤波器后，对方位向做逆傅里叶变换，即可得到RD算法成像结果：
i m g R D = i f f t a { e c h o s 2 ∗ e c h o d 3 m f } img_{RD}=\mathrm{ifft_a}\{{echo}_{s2}*{echo}_{{d3}_{mf}}\} imgRD​=iffta​{echos2​∗echod3mf​​}

CS算法

CS算法基于Scaling原理，通过对chirp信号进行频率调制，实现了对该信号的尺度变换（变标）或平移。基于这种原理可以通过相位相乘替代时域插值完成随距离变化的距离徙动校正，此外，CS算法还能解决二次距离压缩对方位向频率的依赖问题。算法的步骤如下图所示：

第一次相位相乘

在仿真中，将方位向下变频、方位向傅里叶变换和补余距离徙动矫正中的变标(Chirp Scaling)操作纳入到了“第一次相位相乘”这一步骤中。
为了防止方位向发生混叠，同样先对回波信号矩阵$echo$乘上$\exp \left(-2\pi i{f}_{nc}{t}_a\right)$实现方位向下采样，然后计算徙动参数。关于方位向频率改变的徙动参数$D\left(f_a,V_r\right)$的计算方法如：
$$D\left(f_a,V_r\right)=\sqrt{1-\frac{c^2\ast {f_a}^2}{4{V_r}^2\ast {f_0}^2}}$$
关于参考多普勒中心的徙动参数$D\left(f_{nc},V_r\right)$的计算方法如：
$$D\left(f_{nc},V_r\right)=\sqrt{1-\frac{c^2\ast {f_{nc}}^2}{4{V_r}^2\ast {f_0}^2}}$$
变标后的距离向调频率$K_m$为：
$$K_m=\frac{K_r}{1-K_r\ast \left(\frac{c^2\ast t_r\ast {f_a}^2}{4\ast {V_r}^2\ast {f_0}^3\ast {D\left(f_a,V_r\right)}^3}\right)}$$
计算变标方程$S_{sc}\left(\tau ,f_a\right)$：
$$S_{sc}\left(\tau ,f_a\right)=\exp \left(\pi i\ast K_m\ast \left(\frac{D\left(f_{nc},V_r\right)}{D\left(f_a,V_r\right)}-1\right)\ast {\tau }^2\right)$$
对回波信号做方位向傅里叶变换得到信号$ech{o}_{ff{t}_a}$，信号处在距离多普勒域，乘上变标方程$S_{sc}\left(\tau ,f_a\right)$，得到变标后的信号${echo}_{s1}$：
$${echo}_{s1}=ech{o}_{ff{t}_a}\ast S_{sc}\left(\tau ,f_a\right)$$

变标后的信号

CSA算法的灵魂之处在于它的变标操作，在满足以下条件时，变标方程时线性调频的：

1. 发射脉冲为线性调频信号；
2. 等效雷达速度$V_r$不随距离改变；
3. 距离多普勒域中改变后的线性调频率$K_m$不随距离改变。

在信号变标后，利用驻定相位原理计算信号${echo}_{s1}$在二维频域中的表达式可得二维频域信号表达式$S_1(f_{\tau },f_{\eta })$为：
$$\begin{array}{rl}{S}_1\left(f_{\tau },f_{\eta }\right)& =A_1{W}_r(f_{\tau })W_a(f_{\eta }-f_{{\eta }_c})\ast \exp \left\{-i\frac{4\pi R_0{f}_{0}D(f_{\eta },V_r)}{c}\right\}\\ & \\ & \ast \exp \left\{-i\frac{\pi D(f_{\eta },V_r)}{K_{m}D(f_{{\eta }_{ref}},V_r)}{f}_{\tau }^2\right\}\ast \exp \left\{-i\frac{4\pi R_0}{cD(f_{{\eta }_{ref}},V_{r_{ref}})}{f}_{\tau }\right\}\\ & \\ & \ast \exp \left\{-i\frac{4\pi }{c}\left[\frac{1}{D(f_{\eta },V_{r_{ref}})}-\frac{1}{D(f_{{\eta }_{ref}},V_{r_{ref}})}\right]R_{ref}{f}_{\tau }\right\}\\ & \\ & \ast \exp \left\{i\frac{4\pi K_m}{c^2}\left[1-\frac{D(f_{\eta },V_{r_{ref}})}{D(f_{{\eta }_{ref}},V_{r_{ref}})}\right]\ast {\left[\frac{R_0}{D(f_{\eta },V_r)}-\frac{R_{ref}}{D(f_{\eta },V_r)}\right]}^2\right\}\end{array}$$
_{公式复杂正是SAR成像研究的特点，我学的时候也很懵逼(●’◡’●)}

第二次相位相乘

代码中将距离向傅里叶变换、参考函数相乘（用于距离压缩、二次距离压缩和一致距离徙动校正）和距离向傅里叶逆变换划分到“第二次相位相乘的范畴”。
计算距离压缩（一次和二次一起计算）方程${echo}_{{d2}_{mf}}$如下式，该方程用于抵消$S_1(f_{\tau },f_{\eta })$中的第二个指数项：
$${echo}_{{d2}_{mf}}=\exp \left(\frac{\pi i\ast D\left(f_a,V_r\right)\ast {f_r}^2}{K_m\ast D\left(f_{nc},V_r\right)}\right)$$

计算一致距离徙动校正方程${echo}_{{d4}_{mf}}$如下式，用于抵消$S_1(f_{\tau },f_{\eta })$中的第四个指数项：
$${echo}_{{d4}_{mf}}=\exp \left(\frac{4\pi i\ast R_0\ast f_r}{c}\ast \left(\frac{1}{D\left(f_a,V_r\right)}-\frac{1}{D\left(f_{nc},V_r\right)}\right)\right)$$
令上一步处理后的信号做距离向傅里叶变换得到${echo}_{s2}$，信号处在二维频域，然后相乘得到移除了第二和第四个指数项的第二次相位相乘结果${echo}_{s3}$：
$${echo}_{s3}={echo}_{s2}\ast {echo}_{{d2}_{mf}}\ast {echo}_{{d4}_{mf}}$$
对${echo}_{s3}$做距离向逆傅里叶变换得到${echo}_{s4}$，此时信号处在距离多普勒域：
e c h o s 4 = i f f t r { e c h o s 3 } {echo}_{s4}=\mathrm{ifft_r}\{{echo}_{s3}\} echos4​=ifftr​{echos3​}

第三次相位相乘

第三次相位相乘完成方位压缩及相位校正，在代码中将最后的方位向傅里叶逆变换也纳入这一步。
方位向滤波器${echo}_{{d1}_{mf}}$如下式，用于抵消$S_1(f_{\tau },f_{\eta })$中的第一个指数项：
$${echo}_{{d1}_{mf}}=\exp \left(\frac{4\pi i\ast R_{0_{var}}\ast f_0\ast D\left(f_a,V_r\right)}{c}\right)$$
其中，$R_{0_{var}}$为随距离变换的最近点斜距，计算方法如：
$$R_{0_{var}}=\frac{c\ast t_r}{2}$$
变标相位矫正滤波器${echo}_{{d3}_{mf}}$用于抵消$S_1(f_{\tau },f_{\eta })$中的第三项，计算方法如：
$${echo}_{{d3}_{mf}}=\exp \left(\frac{-4\pi i\ast K_m}{c^2}\ast \left(1-\frac{D\left(f_a,V_r\right)}{D\left(f_{nc},V_r\right)}\right)\ast {\left(\frac{R_{0_{var}}}{D\left(f_a,V_r\right)}-\frac{R_0}{D\left(f_a,V_r\right)}\right)}^2\right)$$
令${echo}_{s4}$乘上上述两个滤波器后，沿方位向做逆傅里叶变换即可得到CS算法处理后的成像结果：
$${img}_{CS}={echo}_{s4}\ast {echo}_{{d1}_{mf}}\ast {echo}_{{d3}_{mf}}$$

ωk算法

针对CS算法在宽波束或大斜视角下，近似假设不成立的问题，ωk算法在二维频域通过一种特殊操作来校正距离方位耦合与距离向时间和方位向频率的依赖关系。本仿真采用ωk算法的精确实现版本，流程如下图所示：

ωk算法在二维频域直接完成距离脉压与方位脉压，实现一致压缩，接着利用Stolt插值实现补余压缩，相比于CS算法在形式上更为简单。

参考函数相乘

仿真中将二维傅里叶变换也纳入到“参考函数相乘”这一步。
利用下式生成相位参考函数${\mathrm{theta}}_{{\mathrm{ft}}_{fa}}$，该相位参考函数可同时实现方位向和距离向的匹配滤波:
$${\mathrm{theta}}_{{\mathrm{ft}}_{fa}}=\exp \left\{i\left[\frac{{4\pi R}_0}{c}\sqrt{{\left(f_0+f_r\right)}^2-{\left(\frac{c{f}_a}{2V_r}\right)}^2}+\frac{\pi {f_r}^2}{K_r}\right]\right\}$$
对原始回波信号$echo$做方位向下变频后，执行二维离散傅里叶变换，将回波数据变换到二位频域，并与参考函数$thet{a}_{f{t}_{fa}}$点对点相乘即可实现一致压缩：
e c h o ω k = f f t 2 { e c h o ∗ e x p ( − 2 π i ∗ f n c ∗ t a ) } ∗ t h e t a f t f a {echo}_{\omega k}=\mathrm{fft2}\left\{echo\ast \mathrm{exp}\left(-2\pi i\ast f_{nc}\ast t_a\right)\right\}\ast{\rm theta}_{{\rm ft}_{fa}} echoωk​=fft2{echo∗exp(−2πi∗fnc​∗ta​)}∗thetaftfa​​

Stolt插值

ωk算法通过Stolt插值实现补余压缩，本仿真利用插值函数实现ωk算法的精确版本，利用下式计算映射后的新的距离向频率轴$f_{r_{new}}$：
$$f_{rnew}=\sqrt{{\left(f_0+f_r\right)}^2-{\left(\frac{c{f}_a}{2V_r}\right)}^2}-f_0$$
对于每个方位向，利用“interp1”函数，以$f_r$和$ech{o}_{s}1$作为源数据的x轴和y轴，$f_{rnew}$作为新的x轴，利用三次样条方法实现插值，对位于$f_r$以外的频率点做置0处理，从而实现Stolt插值：
e c h o ω k 2 = i n t e r p 1 { f r , e c h o ω k , f r n e w } {echo}_{\omega k2}=\mathrm{interp1}\left\{f_r,{echo}_{\omega k},f_{rnew}\right\} echoωk2​=interp1{fr​,echoωk​,frnew​}
补余压缩完成后，利用“ifft2”函数将数据变换回时域，即为成像结果：
i m g ω k = i f f t 2 { e c h o ω k 2 } {img}_{\omega k}=\mathrm{ifft2}\left\{{echo}_{\omega k2}\right\} imgωk​=ifft2{echoωk2​}

成像后处理

图像平移与翻转

CS和RD两种算法输出的图像均在方位向上存在空白条带，实验发现该条带的中心与图像方位向下方的距离约为3328像素，该值为多次实验得到，目前尚不清楚如何通过理论计算。利用“circshift”函数对图像矩阵做方位向的循环位移，位移量为-3328，即可将空白带移到方位向边缘。
循环位移后，与说明书参考图像对比发现成像结果上下翻转，利用“flipud”函数对图像矩阵进行上下镜像，即可得到校正后的图像，与参考图几乎一样。

图像增强

亮度钳制

算法直接得到的图像存在亮度不均衡问题，输出像素亮度的频数直方图如下图所示，可见亮度的最大值接近1000，但超过99%的值集中在50以下，因此对输出像素做饱和钳制处理，高于50的像素置为50，实现亮度增强。

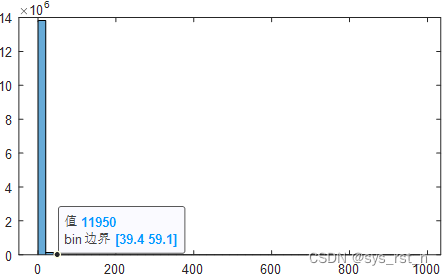
直方图均衡

亮度增强后，还发现图像部分区域过暗，部分区域过亮，存在对比度失衡现象，多次实验后，发现按8*8的大小，限制对比度系数设置为0.004，目标分布设置为正态分布且α为0.5效果最好，利用“adapthisteq”函数即可实现直方图均衡得到最终的成像结果。

仿真实现

代码下载

代码已上传到GitHub: https://github.com/highskyno1/SAR_imaging_with_RD_CS_wk/

成像结果

从下方的成像结果对比可以发现，RD算法存在散焦现象，CS算法和ωk算法成像效果基本一致。观察海上的船只可以发现ωk算法在这种场景下具有更高的像素分辨率，可以看到入海口中间的两艘船的三个光点，相比之下CS算法只能看到一条亮光。

RD算法成像结果

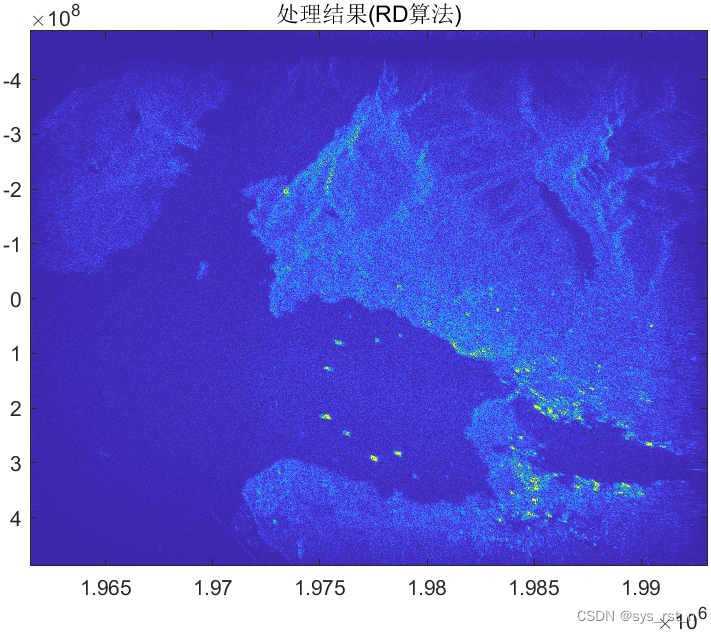
CS算法成像结果

ωk成像结果

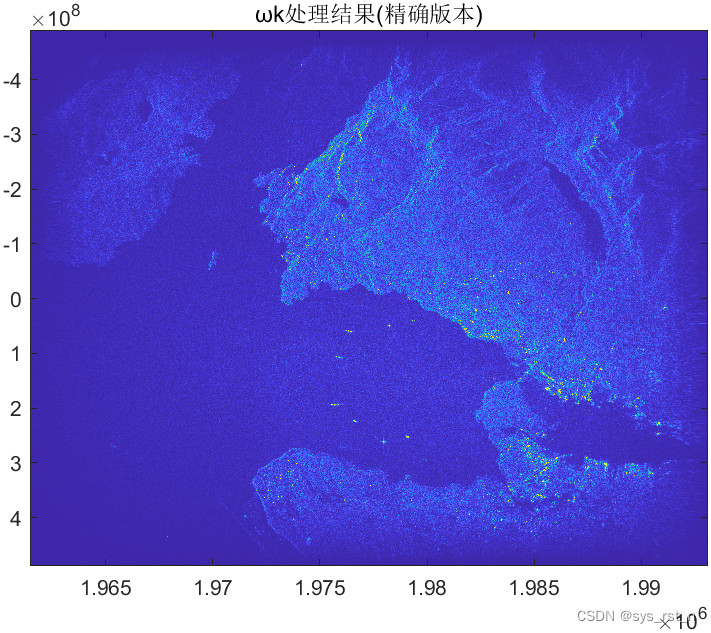
后语

复出第三弹，SAR成像原理与实现奉上。《合成孔径雷达》这门课学习起来的感觉就是公式与概念特别多，还需要雷达信号处理的基础，刚开始去上课的时候每节课听下来还是一脸懵逼，往往课后跟老师交流提问后还是一知半解，最后还是要依靠复现书本的代码才能加深理解。SAR成像的坑特别多，比如频率轴的生成，参数的计算等，在你卡在某一步的时候可以尝试看看公式敲对了没，笔者的经验就是：即使不做徙动校正等操作，只要坐标轴正确，匹配滤波正常，那也还是可以得到有点散焦的结果的，当成像结果花成线条时，一般是某个地方正负号搞反了，或者坐标轴不对。
最后放一张成像结果的灰度图，看到这里了，不妨点个赞再走吧？

附录代码

完整的代码及数据请访问GitHub仓库下载。

RD算法成像

%{
    本代码用于对雷达的回波数据，利用RD算法~普通版本进行成像。
    2023/11/18 20:47
%}
close all;
%% 数据读取
% 加载数据
echo1 = importdata('CDdata1.mat');
echo2 = importdata('CDdata2.mat');
% 将回波拼装在一起
echo = double([echo1;echo2]);
% 加载参数
para = importdata('CD_run_params.mat');
Fr = para.Fr;   % 距离向采样率
Fa = para.PRF;  % 方位向采样率
f0 = para.f0;   % 中心频率
Tr = para.Tr;   % 脉冲持续时间
R0 = para.R0;   % 最近点斜距
Kr = -para.Kr;  % 线性调频率
c = para.c;     % 光速
% 以下参数来自课本附录A
Vr = 7062;      % 等效雷达速度
Ka = 1733;      % 方位向调频率
f_nc = -6900;   % 多普勒中心频率
lamda = c/f0;   % 波长

%% 图像填充
% 计算参数
[Na,Nr] = size(echo);
% 按照全尺寸对图像进行补零
echo = padarray(echo,[round(Na/6), round(Nr/3)]);
% 计算参数
[Na,Nr] = size(echo);

%% 轴产生
% 距离向时间轴及频率轴
tr_axis = 2*R0/c + (-Nr/2:Nr/2-1)/Fr;   % 距离向时间轴
fr_gap = Fr/Nr;
fr_axis = fftshift(-Nr/2:Nr/2-1).*fr_gap;   % 距离向频率轴

% 方位向时间轴及频率轴
ta_axis = (-Na/2:Na/2-1)/Fa;        % 方位向时间轴
ta_gap = Fa/Na; 
fa_axis = f_nc + fftshift(-Na/2:Na/2-1).*ta_gap;    % 方位向频率轴
% 方位向对应纵轴，应该转置成列向量
ta_axis = ta_axis';
fa_axis = fa_axis';

%% 第一步 距离压缩
% 距离向傅里叶变换
echo_s1 = fft(echo,[],2);
% 距离向距离压缩滤波器
echo_d1_mf = exp(1i*pi/Kr.*fr_axis.^2);
% 距离向匹配滤波
echo_s1 = ifft(echo_s1 .* echo_d1_mf,[],2);

%% 第二步 方位向傅里叶变换&距离徙动矫正
% 方位向下变频
echo_s1 = echo_s1 .* exp(-2i*pi*f_nc.*ta_axis);
% 方位向傅里叶变换
echo_s2 = fft(echo_s1,[],1);
% 计算徙动因子
D = lamda^2*R0/8/Vr^2.*fa_axis.^2;
G = exp(4i*pi/c.*fr_axis.*D);
% 校正
echo_s2 = echo_s2.* G;

%% 第三步 方位压缩
% 方位向滤波器
echo_d3_mf = exp(-1i*pi/Ka.*fa_axis.^2);
% 方位向脉冲压缩
echo_s3 = echo_s2 .* echo_d3_mf;
% 方位向逆傅里叶变换
echo_s3 = ifft(echo_s3,[],1);

%% 数据最后的矫正
% 根据实际观感，方位向做合适的循环位移
echo_s4 = circshift(abs(echo_s3), -3328, 1);
% 上下镜像
echo_s4 = flipud(echo_s4);
echo_s5 = abs(echo_s4);
saturation = 50;
echo_s5(echo_s5 > saturation) = saturation;

%% 成像
% 绘制处理结果热力图
figure;
imagesc(tr_axis.*c,ta_axis.*c,echo_s5);
title('处理结果(RD算法)');
% 以灰度图显示
echo_res = gather(echo_s5 ./ saturation);
% 直方图均衡
echo_res = adapthisteq(echo_res,"ClipLimit",0.004,"Distribution","exponential","Alpha",0.5);
figure;
imshow(echo_res);

CS算法成像

%{
    本代码用于对雷达的回波数据，利用CS算法进行成像，利用电平饱和法以及直方图均衡法，
    提高成像质量。
    2023/11/18 11:06
%}
close all;
%% 数据读取
% 加载数据
echo1 = importdata('CDdata1.mat');
echo2 = importdata('CDdata2.mat');
% 将回波拼装在一起
echo = double([echo1;echo2]);
% 加载参数
para = importdata('CD_run_params.mat');
Fr = para.Fr;   % 距离向采样率
Fa = para.PRF;  % 方位向采样率
f0 = para.f0;   % 中心频率
Tr = para.Tr;   % 脉冲持续时间
R0 = para.R0;   % 最近点斜距
Kr = -para.Kr;   % 线性调频率
c = para.c;     % 光速
% 以下参数来自课本附录A
Vr = 7062;      % 等效雷达速度
Ka = 1733;      % 方位向调频率
f_nc = -6900;   % 多普勒中心频率

%% 图像填充
% 计算参数
[Na,Nr] = size(echo);
% 按照全尺寸对图像进行补零
echo = padarray(echo,[round(Na/6), round(Nr/3)]);
% 计算参数
[Na,Nr] = size(echo);

%% 轴产生
% 距离向时间轴及频率轴
tr_axis = 2*R0/c + (-Nr/2:Nr/2-1)/Fr;   % 距离向时间轴
fr_gap = Fr/Nr;
fr_axis = fftshift(-Nr/2:Nr/2-1).*fr_gap;   % 距离向频率轴

% 方位向时间轴及频率轴
ta_axis = (-Na/2:Na/2-1)/Fa;    % 方位向时间轴
ta_gap = Fa/Na; 
fa_axis = f_nc + fftshift(-Na/2:Na/2-1).*ta_gap;    % 方位向频率轴
% 方位向对应纵轴，应该转置成列向量
ta_axis = ta_axis';
fa_axis = fa_axis';

%% 第一步 相位相乘
% 方位向下变频
echo = echo .* exp(-2i*pi*f_nc.*ta_axis);
% 方位向傅里叶变换
echo_fft_a = fft(echo,[],1);
% 计算徙动参数
D_fa_Vr = sqrt(1-c^2*fa_axis.^2/(4*Vr^2*f0^2));  % 关于方位向频率的徙动参数矩阵
D_fnc_Vr = sqrt(1-c^2*f_nc^2/(4*Vr^2*f0^2));    % 关于参考多普勒中心的徙动参数
R0_var = c * tr_axis / 2;    % 随距离变化的最近点斜距
Km = Kr./(1-Kr.*(c*R0_var.*fa_axis.^2./(2*Vr^2*f0^3.*D_fa_Vr.^3))); % 改变后的距离向调频率
% 计算变标方程
tao_new = tr_axis - 2*R0./(c.*D_fa_Vr);   % 新的距离向时间
Ssc = exp(1i*pi*Km.*(D_fnc_Vr./D_fa_Vr - 1).*(tao_new.^2));    % 变标方程
% 补余RCMC中的Chirp Scaling操作
echo_s1 = echo_fft_a .* Ssc;

%% 第二步 相位相乘
% 距离向傅里叶变换
echo_s2 = fft(echo_s1,[],2);
% 补偿第2项
echo_d2_mf = exp(1i*pi*D_fa_Vr.*(fr_axis.^2)./(Km.*D_fnc_Vr));
% 补偿第4项
echo_d4_mf = exp(4i*pi/c*R0*(1./D_fa_Vr-1/D_fnc_Vr).*fr_axis);
% 参考函数相乘用于距离压缩、SRC和一致性RCMC 
echo_s3 = echo_s2 .* echo_d2_mf .* echo_d4_mf;

%% 第三步 相位相乘
% 距离向逆傅里叶变换
echo_s4 = ifft(echo_s3,[],2);
% 方位向匹配滤波
echo_d1_mf = exp(4i*pi*R0_var.*f0/c.*D_fa_Vr);  % 方位向匹配滤波器
% 变标相位矫正
echo_d3_mf = exp(-4i*pi*Km/c^2.*(1-D_fa_Vr./D_fnc_Vr)...
    .*(R0_var./D_fa_Vr-R0./D_fa_Vr).^2);
% 方位向逆傅里叶变换
echo_s5 = ifft(echo_s4 .* echo_d1_mf .* echo_d3_mf,[],1);

%% 数据最后的矫正
% 根据实际观感，方位向做合适的循环位移
echo_s5 = circshift((echo_s5), -3328, 1);
% 上下镜像
echo_s6 = flipud(echo_s5);
% 取模
echo_s7 = abs(echo_s6);
%% 数据可视化
% 绘制直方图
figure;
histogram(echo_s7(:),50);
% 根据直方图结果做饱和处理
saturation = 50;
echo_s7(echo_s7 > saturation) = saturation;
% 绘制处理结果热力图
figure;
imagesc(tr_axis.*c,ta_axis.*c,(echo_s7));
title('处理结果(CS算法)');
% 绘制处理结果灰度图
% 做一些图像处理。。。
echo_res = gather(echo_s7 ./ saturation);
% 直方图均衡
echo_res = adapthisteq(echo_res,"ClipLimit",0.004,"Distribution","exponential","Alpha",0.5);
figure;
imshow(echo_res);

ωk算法成像

%{
    本代码用于对雷达的回波数据，利用wka算法进行成像，利用电平饱和法以及直方图均衡法，
    提高成像质量。
    2023/11/26 21:16
%}
close all;
%% 数据读取
% 加载数据
echo1 = importdata('CDdata1.mat');
echo2 = importdata('CDdata2.mat');
% 将回波拼装在一起
echo = double([echo1;echo2]);
% 加载参数
para = importdata('CD_run_params.mat');
Fr = para.Fr;   % 距离向采样率
Fa = para.PRF;  % 方位向采样率
f0 = para.f0;   % 中心频率
Tr = para.Tr;   % 脉冲持续时间
R0 = para.R0;   % 最近点斜距
Kr = -para.Kr;   % 线性调频率
c = para.c;     % 光速
% 以下参数来自课本附录A
Vr = 7062;      % 等效雷达速度
Ka = 1733;      % 方位向调频率
f_nc = -6900;   % 多普勒中心频率

%% 图像填充
% 计算参数
[Na,Nr] = size(echo);
% 按照全尺寸对图像进行补零
echo = padarray(echo,[round(Na/6), round(Nr/3)]);
% 计算参数
[Na,Nr] = size(echo);

%% 轴产生
% 距离向时间轴及频率轴
tr_axis = 2*R0/c + (-Nr/2:Nr/2-1)/Fr;   % 距离向时间轴
fr_gap = Fr/Nr;
fr_axis = fftshift(-Nr/2:Nr/2-1).*fr_gap;   % 距离向频率轴

% 方位向时间轴及频率轴
ta_axis = (-Na/2:Na/2-1)/Fa;    % 方位向时间轴
ta_gap = Fa/Na; 
fa_axis = f_nc + fftshift(-Na/2:Na/2-1).*ta_gap;    % 方位向频率轴
% 方位向对应纵轴，应该转置成列向量
ta_axis = ta_axis';
fa_axis = fa_axis';

%% 第一步 二维傅里叶变换
% 方位向下变频
echo = echo .* exp(-2i*pi*f_nc.*ta_axis);
% 二维傅里叶变换
echo_s1 = fft2(echo);
%% 第二步 参考函数相乘(一致压缩)
% 生成参考函数
theta_ft_fa = 4*pi*R0/c.*sqrt((f0+fr_axis).^2-c^2/4/Vr^2.*fa_axis.^2)+pi/Kr.*fr_axis.^2;
theta_ft_fa = exp(1i.*theta_ft_fa);
% 一致压缩
echo_s2 = echo_s1 .* theta_ft_fa;

%% 第三步 在距离域进行Stolt插值操作(补余压缩)
% 计算映射后的距离向频率
fr_new_mtx = sqrt((f0+fr_axis).^2-c^2/4/Vr^2.*fa_axis.^2)-f0;
% Stolt映射
echo_s3 = zeros(Na,Nr);
t = waitbar(0,'Stolt映射中');
for i = 1:Na
    if mod(i,10) == 0
        waitbar(i/Na,t);
    end
    echo_s3(i,:) = interp1(fr_axis,echo_s2(i,:),fr_new_mtx(i,:),"spline",0);
end
close(t);

%% 第四步 二维逆傅里叶变换
echo_s4 = ifft2(echo_s3);

%% 第五步 图像纠正
echo_s5 = circshift(echo_s4,-1800,2);
echo_s5 = circshift(echo_s5,-3365,1);
echo_s5 = flipud(echo_s5);

%% 画图
saturation = 50;
figure;
echo_s6 = abs(echo_s5);
echo_s6(echo_s6 > saturation) = saturation;
imagesc(tr_axis.*c,ta_axis.*c,echo_s6);
title('ωk处理结果(精确版本)');
% 绘制处理结果灰度图
% 做一些图像处理。。。
echo_res = gather(echo_s6 ./ saturation);
% 直方图均衡
echo_res = adapthisteq(echo_res,"ClipLimit",0.004,"Distribution","exponential","Alpha",0.5);
figure;
imshow(echo_res);

---

1. 合成孔径雷达成像算法与实现/(加)伊恩·G. 卡明(Ian G. Cumming)等著; 洪文等译. —北京: 电子工业出版社, 2019. 7 ↩︎