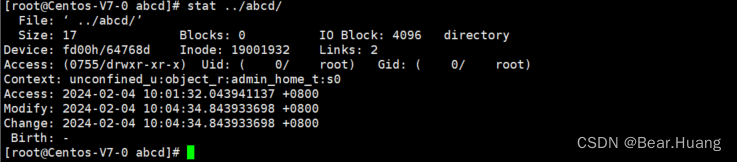
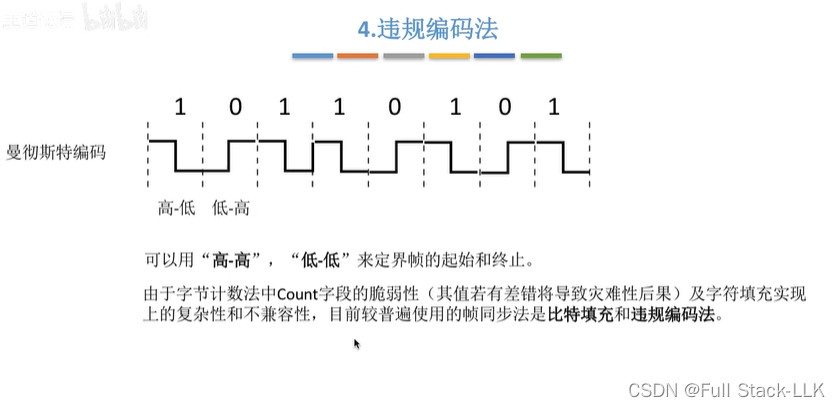
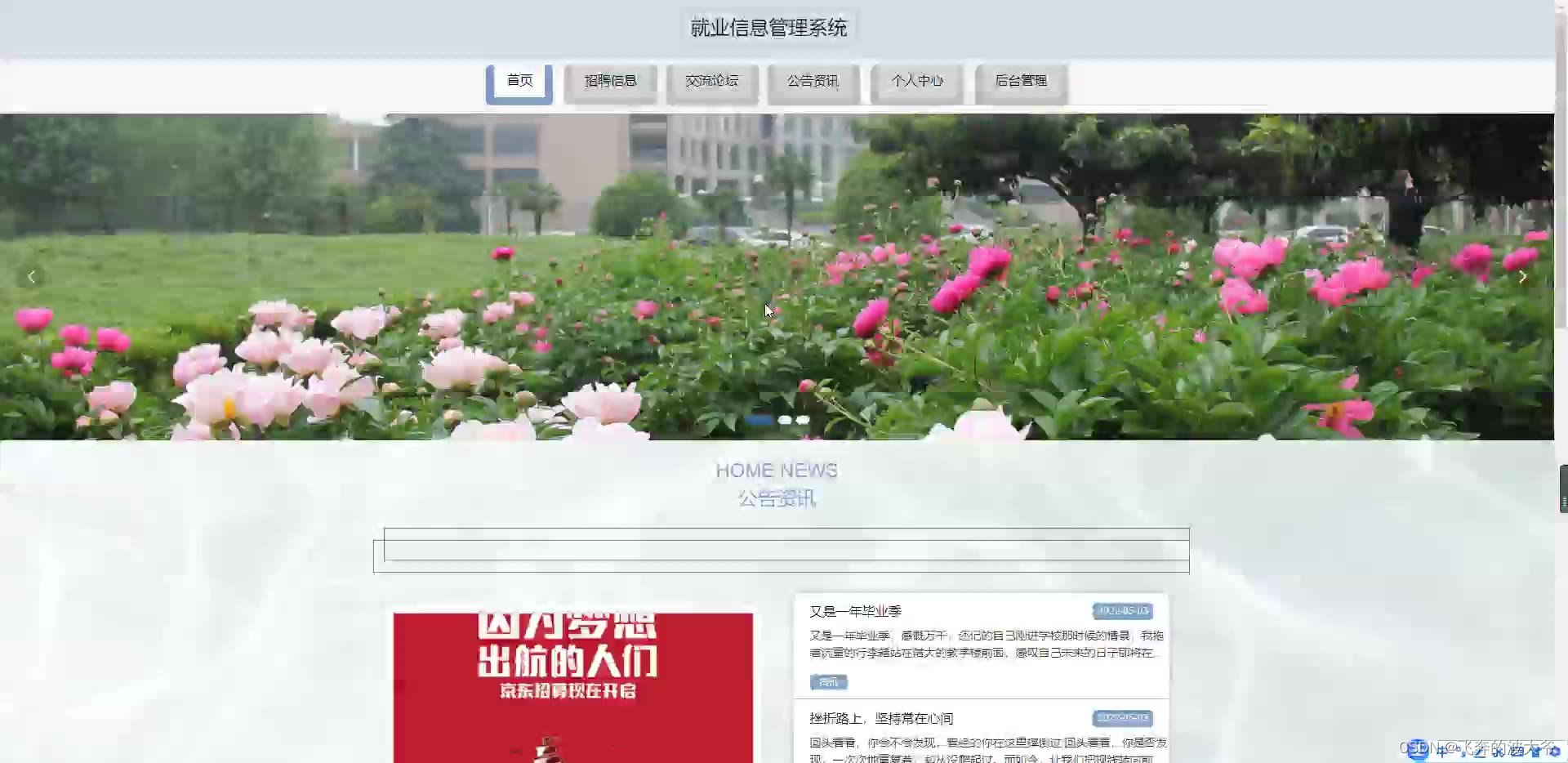
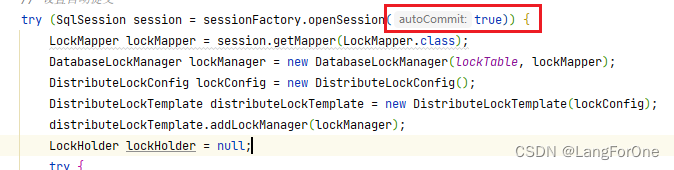
接下来,我们先学习一个概念,带有权值的图,其实就是每条边上有一个自己独立的值了,接下来我们来进行一个深入的了解吧。
1.带权值得的图的概念
在前面的课程中,图中的边都只是用来表示两个点之间是否存在关系,而没有体现出两个点之间关系的强弱。比如在社交网络中,不能单纯地用 0、1 来表示两个人否为朋友。当两个人是朋友时,有可能是很好的朋友,也有可能是一般的朋友,还有可能是不熟悉的朋友。
我们用一个数值来表示两个人之间的朋友关系强弱,两个人的朋友关系越强,对应的值就越大。而这个值就是两个人在图中对应的边的权值,简称 边权。对应的图我们称之为 带权图。
如下就是一个带权图,我们把每条边对应的边权标记在边上:
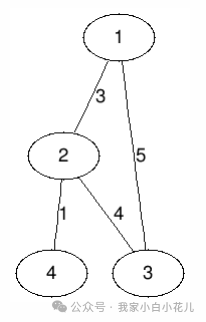
接下来我们呢先来讲解一下邻接矩阵该怎么来进行储存带权值的图
2.邻接矩阵进行储存
带权图也分成带权有向图和带权无向图。前面学到的关于图的性质在带权图上同样成立。实际上,我们前面学习的图是一种特殊带权图,只不过图中所有边的权值只有
1 一种;而在带权图中,边的权值可以是任意的。
用邻接矩阵存储带权图和之前的方法一样,用G[a][b]来表示 a 和 b 之间的边权(我们需要用一个数值来表示边不存在,如0)。同样,对于无向图,这个矩阵依然是对称的。
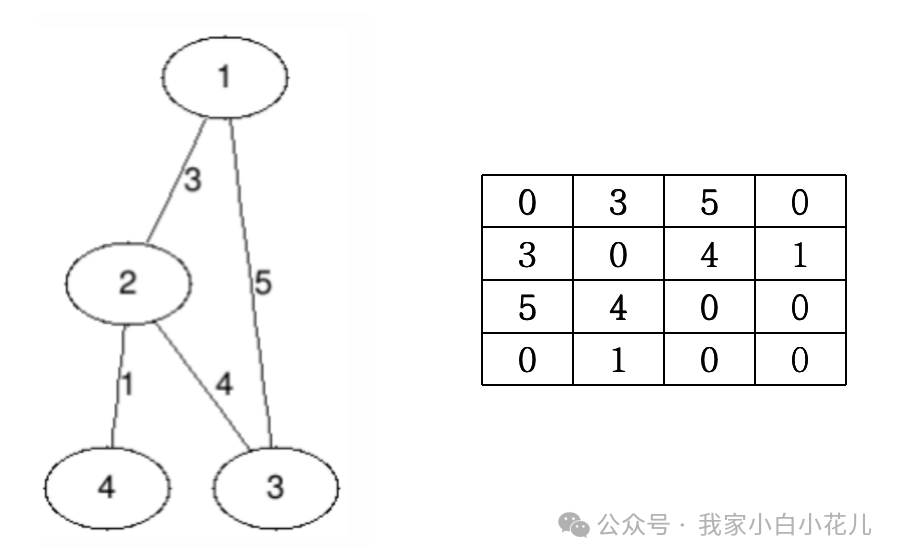
如上所示,左边的图对应的右边的邻接矩阵。
3.对于邻接表...
用邻接表存储带权图和之前的实现方式有区别,我们需要用一个结构体来记录一条边连接的点和这条边的边权,然后用一个vector来存储若干个结构体,
实际上就是把一个点所连接的点以及这条边的边权"打包"起来放到邻接表中。
结构体的定义举例如下:
struct node {
int v; // 用来记录连接的点
int w; // 用来记录这条边的边权
};我们通常把有向图中加入一条边写成一个函数,例如加入一条 有向边
(u,v)、边权为 w,就可以用如下的函数来实现(我们需要把图定义成全局变量)。
vector<node> G[105];
// 插入有向边
void insert(int u, int v, int w) {
node temp;
temp.v = v;
temp.w = w;
G[u].push_back(temp);
}而插入一条无向边,实际上相当于插入两条方向相反的有向边:
// 插入无向边
void insert2(int u, int v, int w) {
insert(u, v, w);
insert(v, u, w);
}