一、题目

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

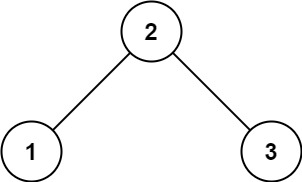
输入：root = [2,1,3]
输出：true

示例 2：

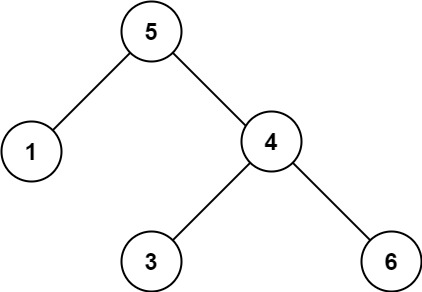
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

二、思路解析

开始我先说这道题要用到的一条定理：二叉搜索树的中序遍历，其结果是一个递增序列。

证明过于简单，画图即可，在此不做赘述。

二叉树的例题，我们都得先判断这棵树是否为空树，也就是 root 是否为 null ，是的话返回 true 即可，因为这也是符合题目要求的一颗二叉搜索树。

而具体的实现，就需要用到刚开头提到的定理，做一个中序遍历。

因此，首先递归调用函数本身，把 root. left 传过去。

注意这里可以做一个优化：定义一个布尔类型变量，用于接受我们刚刚的递归调用，如果返回的是 false ，那就证明他左子树中有元素大于根节点，不满足二叉搜索树的定义，直接 return 掉。

这步优化也就是所谓的 剪枝 。

按照中序遍历，接下来依次轮到根节点和右子树了，先定义一个 cur 节点来判断根节点是否大于其左子树的值，是的话返回 true ，反之亦然。

然后也是一步剪枝操作来优化。

这里有一个小细节， “左子树的值” 我在开始的时候定义成了全局变量，省去了每一次递归都要传值的繁琐。

最后就是右子树的遍历了，同样也是递归调用函数本身，跟左子树区别仅在于传值的不同。

具体实现请看下面代码👇

三、完整代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {

    long prev = Long.MIN_VALUE;

    public boolean isValidBST(TreeNode root) {
        if(root == null){
            return true;
        }

        boolean left = isValidBST(root.left);
        
        // 剪枝            
        if(left == false){
            return false;
        }

        boolean cur = false;
        if(root.val > prev){
            cur = true;
        }

        // 剪枝
        if(cur == false){
            return false;
        }        

        prev = root.val;
        boolean right = isValidBST(root.right);

        return left && cur && right;
    }
}

以上就是本篇博客的全部内容啦，如有不足之处，还请各位指出，期待能和各位一起进步！