目录
树的种类
二叉树
二叉查找树
满二叉树
编辑
完全二叉树
二叉树的数据存储
链式存储
数组存储
寻址方式:
二叉树的遍历(了解即可)
编辑
二叉查询树缺点
前言-与正文无关
生活远不止眼前的苦劳与奔波,它还充满了无数值得我们去体验和珍惜的美好事物。在这个快节奏的世界中,我们往往容易陷入工作的漩涡,忘记了停下脚步,感受周围的世界。让我们一起提醒自己,要适时放慢脚步,欣赏生活中的每一道风景,享受与家人朋友的温馨时光,发现那些平凡日子里隐藏的幸福时刻。因为,这些点点滴滴汇聚起来的,才是构成我们丰富多彩生活的本质。希望每个人都能在繁忙的生活中找到自己的快乐之源,不仅仅为了生存而工作,更为了更好的生活而生活。
送你张美图!希望你开心!

树的种类

旧金山的数据结构可视化助你了解算法数据结构的变化。
Data Structure Visualization
二叉树
二叉查找树
当然我们最常说的二叉树就二叉查找树也叫二叉排序树。下面讲的满二叉树和完全二叉树其实了解一下即可,不常说常用!
任意非空二叉查找树,必定满足左子节点值 < 根节点值;根节点值 < 右子节点值 ,没有键值相等的节点
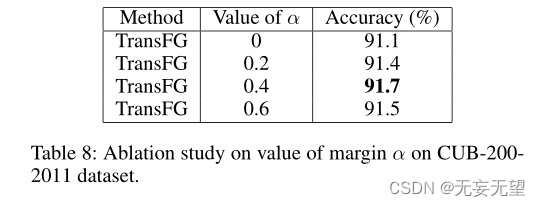
在二叉查找树中查找 N ,首先从根节点开始,将根节点设置为第一个访问的节点,若当前节点为空,则查找失败,若 N 与当前节点值相等,返回当前节点,若 N 大于当前节点值,则从当前节点的右子节点开始查找,否则从当前节点的左子节点开始查找,直到返回目标节点或者查找失败;如下图在二叉查找树中查找目标 8 ,查找路径依次为 ⑨ --> ⑥ --> ⑦ --> ⑧
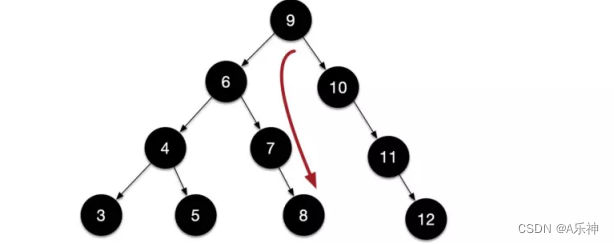
满二叉树
完全二叉树
区别:
二叉树的数据存储
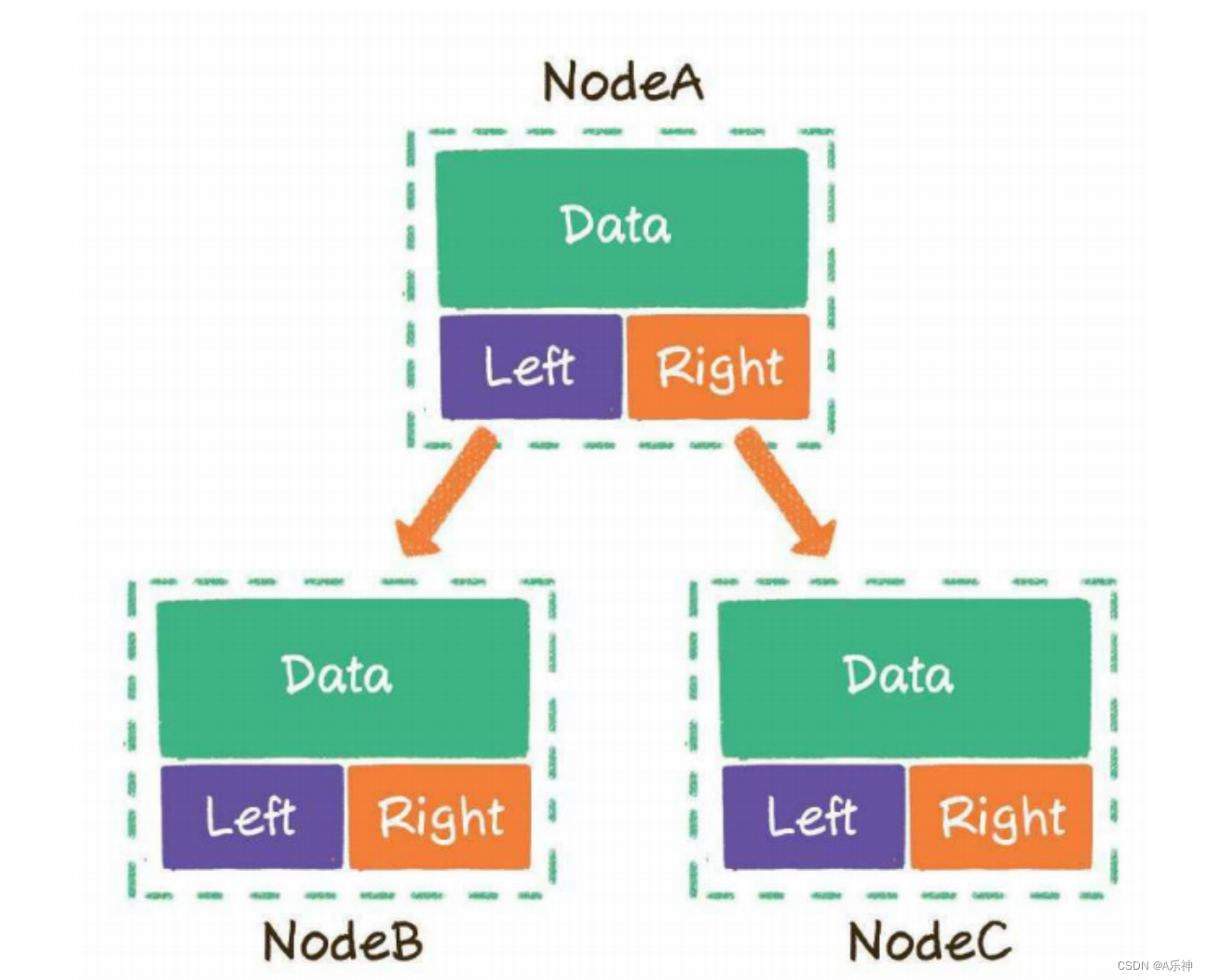
链式存储
数组存储

寻址方式:
二叉树的遍历(了解即可)
二叉树遍历拥有三种实现类方法
前序遍历【DLR】:前序遍历也叫先根遍历,先访问根节点然后遍历左子树,最后遍历右子树;

中序遍历【LDR】:中序遍历也叫中根遍历,先遍历左子树然后访问根节点,最后遍历右子树;
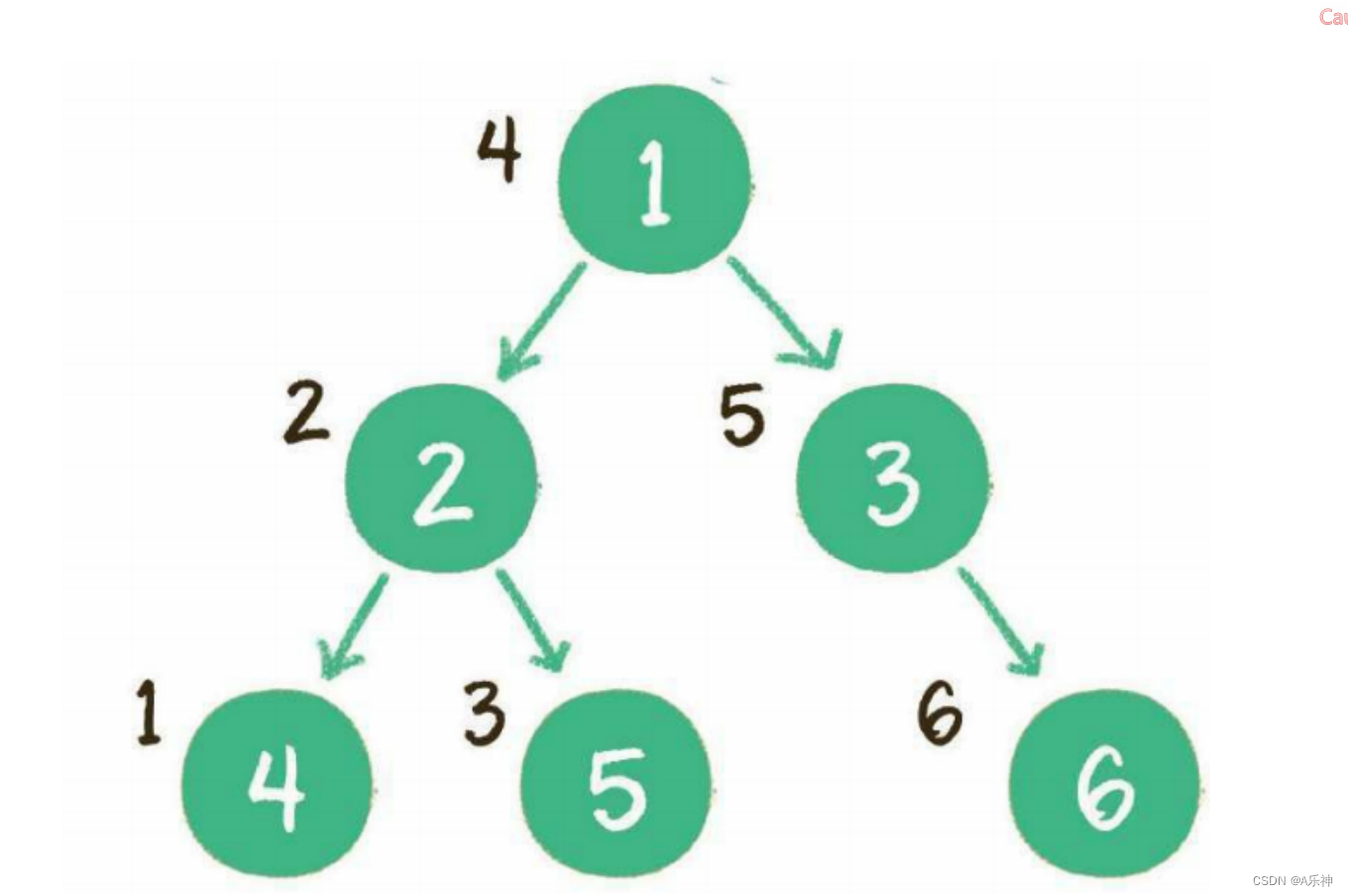
后序遍历【LRD】:后序遍历也叫后根遍历,先遍历左子树然后遍历右子树,最后访问根节点;
二叉查询树缺点
有了二叉查询树为什么要使用平衡二叉查找树 呢?
二叉查找树并非平衡树,它只限制了左右子树与根点之间的大小关系,只有在平衡二叉查找树时,其时间复杂度才能达到 O(logn) ,并且在极端情况下它甚至会退化成链表;在不平衡的情况下就要遍历比对多次。
如下所示在新创建的二叉查找树上依次添加数据 1、2、3、4、5、6、7、8、9、10 节点,此二叉查找树就退化成了链表,增删查性能也退化到了 O(n)。
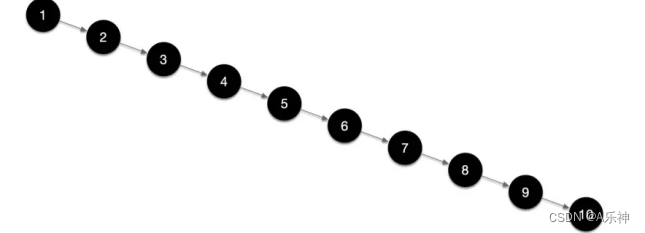
所以为了避免这种情况,就出现了 AVL 及红黑树这种能自平衡的二叉查找树;AVL 树是严格的平衡二叉树,必须满足所有节点的左右子树高度差不超过 1;
详情我的下一章:Java 数据结构 二叉树(二)
------------------------------------------与正文内容无关------------------------------------
如果觉的文章写对各位读者老爷们有帮助的话,麻烦点赞加关注呗!作者在这拜谢了!
混口饭吃了!如果你需要Java 、Python毕设、商务合作、技术交流、就业指导、技术支持度过试用期。请在关注私信我,本人看到一定马上回复!
这是我全部文章所在目录,看看是否有你需要的,如果遇到觉得不对地方请留言,看到后我会查阅进行改正。
A乐神-CSDN博客











![[Tomcat问题]--使用Tomcat 10.x部署项目时,出现实例化Servlet类[xxx]异常](https://img-blog.csdnimg.cn/img_convert/dad5cef90b1200f27f051ee7335444ec.png)