机器学习周记（第二十八周：文献阅读-GSTPro）2024.1.29~2024.2.4

摘要

ABSTRACT

1 论文信息

1.1 论文标题

1.2 论文摘要

1.3 论文背景

2 论文模型

2.1 问题描述

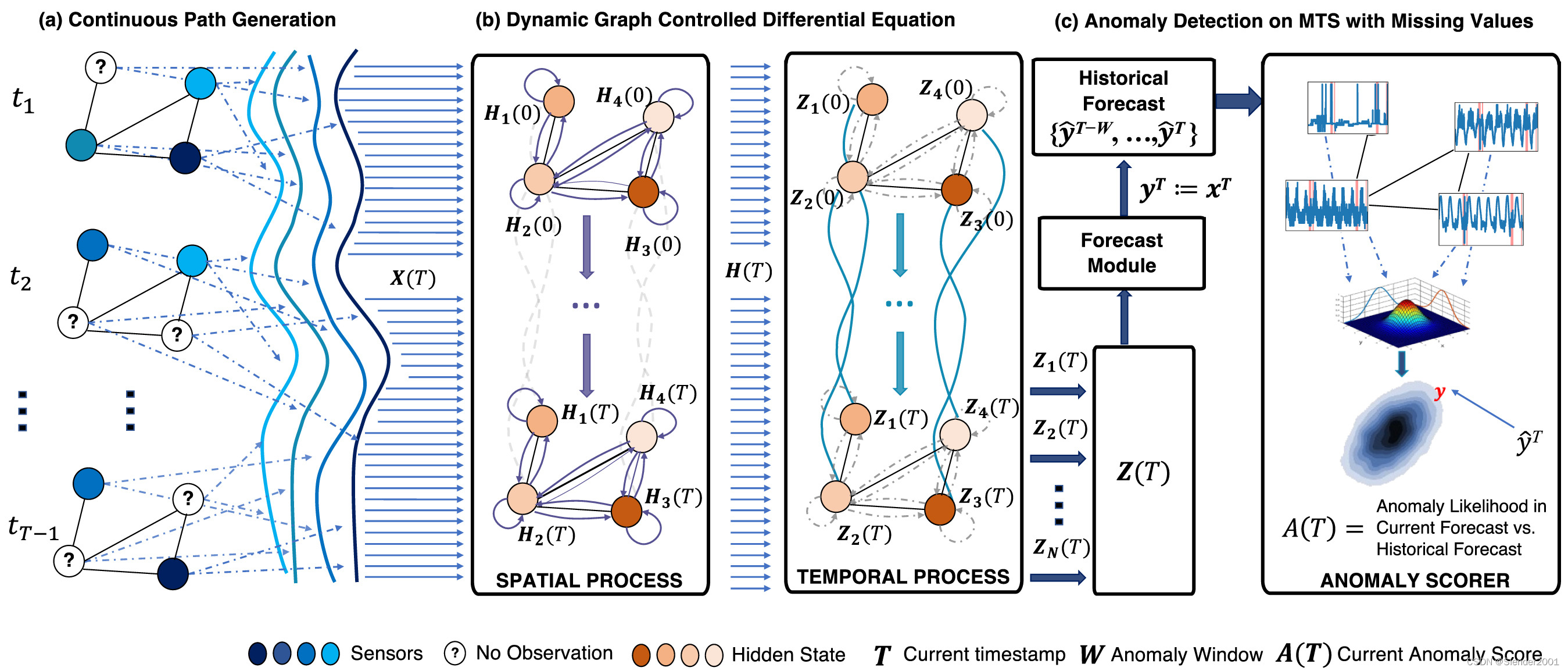
2.2 总体架构

2.3 动态图神经控制微分方程（Dynamic Graph Neural Controlled Differential Equations）

2.3.1 空间处理（Spatial Process）

2.3.2 时间处理（Temporal Process）

2.4 异常评分（Anomaly Scoring）

2.5 模型训练（Model Training）

3 相关代码

摘要

本周阅读了一篇关于使用图时空神经网络和异常评分器来解决在非规则采样的多元时间序列上检测异常的论文。图时空处理主要基于神经控制微分方程，从空间和时间角度对多元时间序列进行有效建模，即使数据中包含缺失值。异常评分器主要基于高斯分布，不需要与真实值进行比较，避免了在计算异常评分时因缺失值而产生的问题，其次它完全基于预测统计，不包含可训练参数。异常评分器的主要原理是将当前预测值与历史预测值进行比较，计算异常可能性。

ABSTRACT

This week, We read a paper on using graph spatiotemporal neural network and anomaly scorers to detect anomalies in irregularly sampled multivariate time series. The graph spatiotemporal processing is primarily based on neural controlled differential equations, effectively modeling multivariate time series from spatial and temporal perspectives, even when the data contains missing values. The anomaly scorer is mainly based on Gaussian distribution, eliminating the need for comparisons with real values, thereby avoiding issues related to missing values in computing anomaly scores. Additionally, it relies entirely on predictive statistics and does not include trainable parameters. The core principle of the anomaly scorer is to compare the current predicted value with historical predicted values to calculate the likelihood of anomalies.

1 论文信息

1.1 论文标题

1.2 论文摘要

多元时间序列数据中的异常检测在智能电网、交通流量预测、工业流程控制等诸多实际应用中具有重要意义。然而，现实世界的时间序列数据通常结构不完善，对后续的时间序列处理任务带来了如下挑战：(1)多元时间序列数据中缺失值的存在阻碍了对相互交织的时空依赖关系的有效建模，导致重要模式在模型训练过程中被忽略；(2)对不规则采样观测值的异常评分的探索较少，使得现有的检测机制难以用于没有完整观测值的多元序列。本文提出一种新的框架GST-Pro，利用图时空处理和异常评分器来解决上述在非规则采样的多元时间序列上检测异常的挑战。该方法由两个主要部分组成。首先，提出一种基于神经控制微分方程的图时空处理。该处理使得从空间和时间角度对多元时间序列进行有效建模成为可能，即使数据中包含缺失值。其次，提出了一种新的基于高斯分布的异常评分机制，减轻了对完全均匀观测的依赖。通过分析图时空处理的预测，该方法能够轻松检测异常。实验结果表明，无论数据中是否存在缺失值，GST-Pro方法都可以有效地检测时间序列数据中的异常，其性能优于现有方法。

1.3 论文背景

随着技术的飞速进步，时间序列数据的广泛性和数据量呈现爆炸式的增长。从医疗保健和关键基础设施到航天器，各个行业目前正在从大量设备或传感器跨时间产生数据，形成具有数百到数千个变量的复杂多元时间序列。多元时间序列数据的激增不可避免地导致我们严重依赖通过多元时间序列数据自动检测异常事件，以识别、避免和响应灾难性事件发生之前和发生时的状况。理想情况下，检测可以通过允许大规模实施的算法来完成，并且对现实世界系统产生的噪声具有鲁棒性。因此，开发鲁棒多元时间序列异常检测模型的需求日益迫切。尽管有大量的多元时间序列数据表现出正常模式，但异常事件通常与罕见事件相关，因此收集和标记异常通常是一项艰巨的任务，也因此，无监督异常检测技术作为解决异常检测问题的一种实用方法被广泛探索。在已提出的方法中，经典的方法包括统计无监督模型，如ARIMA/VAR、基于距离或分布的方法。然而，这些方法在捕捉多元时间序列数据中存在的非线性时空关系方面存在一定的局限性。

最近，随着深度学习（DL）的蓬勃发展，该领域目前取得了重大进展。一项早期的工作提出了一种使用长短期记忆（LSTM）网络来根据预测误差检测异常的方法。然而，LSTM框架缺乏对变量对间相互依赖关系的显式建模，限制了其在高维多变量时间序列数据中检测复杂异常事件的能力。为此，mtat-gat和GDN使用时空图神经网络（STGNNs）对时空数据相关性进行建模。特别是GDN，它使用图学习层来学习成对的相关性，不需要预定义的图。到目前为止，STGNNs仍然是最先进的多元时间序列异常检测模型。尽管在多元时间序列异常检测方面取得了重大进展，但现有的深度异常检测技术依赖于以均匀频率采样的结构良好且规则的时间序列数据。然而，由于采样频率的不规则性，现实世界的多元时间序列数据往往存在随机缺失值或非均匀观测值。多变量时间序列数据中的随机缺失值通常是由于传感器限制或传输中断造成的，而非随机缺失值则可能由多模态源和过程异构造成。即使对于小规模系统，随机缺失值几乎也是不可避免的。因此，开发出能够准确检测异常事件的鲁棒技术至关重要。而现实是，不规则多元时间序列异常检测问题迄今为止还没有得到很好的研究。

为了解决缺失的数据点，可以使用最直接的解决方案，比如零填充、插值算法、插补算法和线性预测器。这样，多元时间序列中的缺失值问题可以简单地作为预处理步骤来解决。然而，论文的实验结果所表明的，使用插补然后检测这样模块化的流水线方法可能会大大削弱异常检测性能。这需要一种替代方法来检测不规则多元时间序列中的异常事件。具有缺失值的多元时间序列中检测异常任务图示如Fig.1所示。按照标准的无监督异常检测设置，正常数据的前六个观测值用于训练模型，而测试数据包含正常(第一个和最后一个)和异常(中间四个)时间戳，用于评估模型检测异常的能力。其中红圈数据代表异常数据。

首先，A1序列没有异常事件，但会间歇性地记录一个短突发值，虽然这在规则序列设置中很容易学习，但不规则多元时间序列在正常训练期间可能不会记录短突发，模型可能会认为这些短突发事件在检测测试期间是异常的。总之，在缺失值情况下，用于无监督学习的高质量训练数据是稀疏的。其次，如右图B1所示，在异常时段真实观测值可能缺失，导致数据异常检测困难。因此，不能依靠真实的观测值来实时检测异常事件。A1和B1都是一个时间序列，记录了独立移动的值。然而，在多元时间序列中，变量之间存在着错综复杂的联系。例如，C1、C2和C3是相互关联的变量，其中C1与C2呈强负相关，而C3与C2呈强正相关。因此，偏离这些关系是一种异常事件。在Fig.1的右图中，可以看到C1只在前两个早期时间点记录了与C2冲突的值，但随后的异常值没有记录。与此相反，C3记录的异常值发生在后期，而不是早期。由于在随机缺失场景下，不太可能出现所有通道同时存在缺失值的情况，因此作者推测，如果一个模型充分捕捉了变量之间的相互依赖关系，那么在不规则多元时间序列中，即使数据存在高缺失率，也能很好地检测异常事件。因此，对于异常检测模型来说，显式地捕获多元时间序列中变量之间复杂的成对关联关系（即空间依赖程度）至关重要。

2 论文模型

为应对这些挑战，本文提出一种新的基于预测的异常评分器，利用图时空处理对多元时间序列进行建模，无论它们是否包含缺失值。具体来说，该方法涉及对输入多变量时间序列的每个变量中的缺失值进行插补，以生成完整的连续序列。设计了两个神经控制微分方程（NCDE）过程，从空间和时间角度对输入数据进行建模，同时解决了上述第一和第三个挑战。通过结合这些过程，我们能够对任何多元时间序列进行建模，而不管它们是否包含缺失值。为应对第二个挑战，本文提出一种新的基于分布的异常评分器，其建立在时间序列模型之上具有两个显著优势：(1)仅基于模型预测，不需要与真实值进行比较，避免了在计算实时异常评分时因缺失值而产生的问题；(2)它完全基于预测统计，不包含可训练参数，使其成为一个即插即用模块，甚至可以与论文方法之外的其他时间序列模型集成。通过结合前文讨论的预测器和异常评分器，所提出的GST-Pro方法可以在线、无监督地有效检测现实世界任意多变量时间序列数据中的异常，如Fig.2所示。

2.1 问题描述

具有连续等间隔观测值的多元时间序列可以定义为 $X=\left \{ X^{(1)},X^{(2)},...,X^{(T)} \right \}$ ，其中 $T$ 表示当前时间戳的序列长度， $X^{(t)}\in \mathbb{R}^{N}$ 由 $N$ 个单变量通道 $\left \{ x_{1}^{(t)}, x_{2}^{(t)},..., x_{N}^{(t)} \right \}$ 组成。因此，每个单变量通道也可以互换，并称为“传感器”或“节点”。对于常规的无监督多元时间序列异常检测，我们需要学习一个异常分类器或评分器 $A(\cdot)$ ，该分类器向每个时间戳输出一个异常分数，该分数可以清楚地区分异常观测值和非异常观测值。特别地，输出可以概念化为一个指示器，告知系统操作员时间戳是否异常， $A(X^{(a)})> A(X^{(n)})$ ，其中 $X^{(a)}$ 是异常观测值， $X^{(n)}$ 不是。表示时间戳是否异常的基准值标签表示为 $g^{(t)}\in \left \{ 0,1 \right \}$ ，如果观测值 $X^{(t)}$ 异常，则表示为 $g^{(t)}=1$ 。由于异常检测是在数据实时流化时发生的，因此模型只能依靠过去的观察值在每个时间戳上做出决策，而不能逆转之前的决策。对于非规则无监督多元时间序列异常检测，作者的目标是在数据中存在缺失值的情况下达到同样的目标。注意本文考虑随机缺失场景，缺失值问题存在于用于无监督训练的训练数据和用于评估异常事件检测模型的测试数据中。这种不规则性在实际的多元时间序列中很常见，因此是本文工作的重点。

2.2 总体架构

GST-Pro的架构，包括两个关键组件：基于DG-NCDE的预测头和基于高斯评分的异常检测器。主要的处理步骤如下：(a)对缺失值对进行插补以生成连续序列；(b)利用两个神经控制微分方程从空间和时间角度处理输入信号；(c)使用基于高斯分布的评分器对任意多元时间序列进行实时异常检测，该评分器根据预测输出评估异常，而无需真实观测值。异常得分是通过使用多元正态分布评估当前预测与历史预测的偏差可能性来计算的。

2.3 动态图神经控制微分方程（Dynamic Graph Neural Controlled Differential Equations）

多元时间序列通常被概念化为由规则采样的图快照组成的离散时间动态图，记为 $G_{t}:=(V,E,X^{(t)})$ 。在这里， $V$ 和 $E$ 为序列预定义的图结构，描述了变量（传感器）之间的潜在连通性，而 $X^{(t)}$ 指快照 $G_{t}$ 在时间 $t$ 的节点特征。由于数据采样或传感器故障，变量维度和时间维度都可能存在缺失值。本文提出的动态图神经控制微分方程（DG-NCDE）对多元时间序列进行建模，可以不管数据中是否存在缺失值。神经控制微分方程（NCDEs）的表述如Eq.(1)所示，其最终目标是从数据中学习一个CDE函数 $f(\cdot;\Theta )$ ，参数为 $\Theta$ 。

2.3.1 空间处理（Spatial Process）

首先从由连续序列 $\widetilde{X}(t)$ 控制的消息传递角度对每个变量在图快照之间的隐藏状态演变进行建模。

2.3.2 时间处理（Temporal Process）

2.4 异常评分（Anomaly Scoring）

GST-Pro可以在每个时间戳上评估异常，而不需要访问其对应的真实观测值。具体来说，在当前时间戳 $T$ ，GST-Pro的异常评分器所需的唯一输入是来自预测模块的当前和历史预测值 $\left \{ \widehat{y}^{(1)},...,\widehat{y}^{(T)} \right \}$ 。

GST-Pro的异常评分器仅考虑预测输出，而不考虑重构或预测误差。虽然预测误差允许基于预测值与实际值之间的偏差简单地检测异常事件，但在不规则的时间序列场景下，由于缺失值和无法访问，实际观察结果不够可靠。相反，在非异常期间GST-Pro可以预测与预测值非常相似的值，而在异常期间生成与正常预测输出不同的输出。换句话说，只要输入滑动窗口的信号存在空间和或时间上的异常，GST-Pro应该生成异常的预测。相反，如果输入中没有异常信号，它应该生成类似于非异常训练数据的预测输出。这种方法不需要做任何假设，除非是为了准确地填补缺失值。作者将重要性放在GST-Pro的预测模块上，从训练数据中学习空间和时间依赖性的正常性。

2.5 模型训练（Model Training）

虽然论文所提出的异常检测器不包含可训练参数，但所提出的DG-NCDE预测模块需要无监督训练。为了实现这一点，构建下面的增广ODE，而不是单独实现Eq.(3)、Eq.(5)：

$\frac{d}{dt}\begin{bmatrix} Z(t) \\ H(t) \end{bmatrix}= \begin{bmatrix} f(Z(t);\Theta )g(H(t);\Phi )\frac{d\widetilde{X}(t)}{dt} \\ g(H(t);\Phi )\frac{d\widetilde{X}(t)}{dt} \end{bmatrix}$ ，（9）

$H(0)=FC(\widetilde{X}(t_{0}))$ ， $Z(0)=FC(H(0))$ 分别为两个NCDE函数的初始化值，使用 $Z(\zeta )$ 得到单步预测： $\widehat{y}=FC(Z(\zeta ))\in \mathbb{R}^{N}$ ，其中 $N$ 是MTS中通道的数量。

GST-Pro通过如下损失函数优化参数： $L=\frac{\sum_{i=1}^{N}m_{i}^{(t)}\cdot\left \| y^{(t)}_{i}-\widehat{y}^{(t)}_{i} \right \| _{1}}{\left |N \right |}$ 。 $y_{(i)}$ 和 $\widehat{y}_{(i)}$ 分别代表节点 $i$ 的真实值和预测值。 $m^{(i)}_{t}\in \left \{ 0,1 \right \}$ 表示在时间戳 $t$ 是否值缺失， $m^{(t)}_{i}\in M$ ， $M\in \left \{ 0,1 \right \}^{N}$ 。

3 相关代码

NCDE时间序列预测示例：

import torch
import torchcde

# 创建一个简单的时间序列
batch, length, input_channels = 1, 10, 2
hidden_channels = 3
t = torch.linspace(0, 1, length)
t_ = t.unsqueeze(0).unsqueeze(-1).expand(batch, length, 1)
x_ = torch.rand(batch, length, input_channels - 1)
x = torch.cat([t_, x_], dim=2)  # include time as a channel

# 使用自然三次样条插值法插值序列
coeffs = torchcde.natural_cubic_spline_coeffs(x)
X = torchcde.NaturalCubicSpline(coeffs)

# 创建NCDE模型
class F(torch.nn.Module):
    def __init__(self):
        super(F, self).__init__()
        self.linear = torch.nn.Linear(hidden_channels, 
                                      hidden_channels * input_channels)
    def forward(self, t, z):
        return self.linear(z).view(batch, hidden_channels, input_channels)

func = F()
z0 = torch.rand(batch, hidden_channels)

torchcde.cdeint(X=X, func=func, z0=z0, t=X.interval)