一共有这么几个题目，主要是用来表现题目的性质
分别是求

二叉树节点个数
二叉树叶子节点个数
二叉树第k 层节点个数
二叉树查找值为x 的节点

如果我使用的还是这个二叉树

其中 NULL 表示终止

二叉树节点个数

图解过程

总个数 = 根节点个数 + 左子树个数 + 右子树个数

整个过程

程序实现

int countNode(TreeNode* root)
{
	if(root == NULL)
	{
		return 0;
	}
	return 1+countNode(root->left)+count(root->right);
}

二叉树叶子节点个数

叶子节点，是这个节点之后没有其他节点了

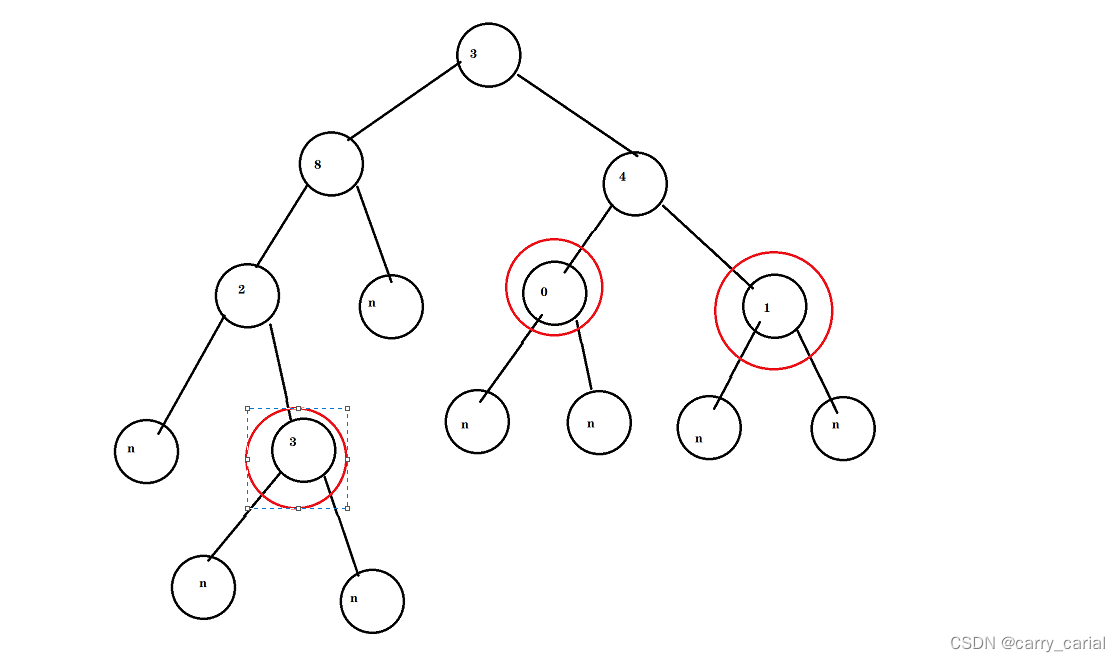
红圈就是叶子节点
因此只要返回 左右节点都是 NULL 的节点就可以了

程序

int countleaf(TreeNode* root)
{
	if(root == NULL)
	{
		return 0;
	}
	if(root -> left == NULL && root ->right == NULL)
	{
		return 1;
	}
	return countleaf(root->left) + countleaf(root->right);
}

二叉树第k 层节点个数

二叉树能够分层，每一层有对应的个数

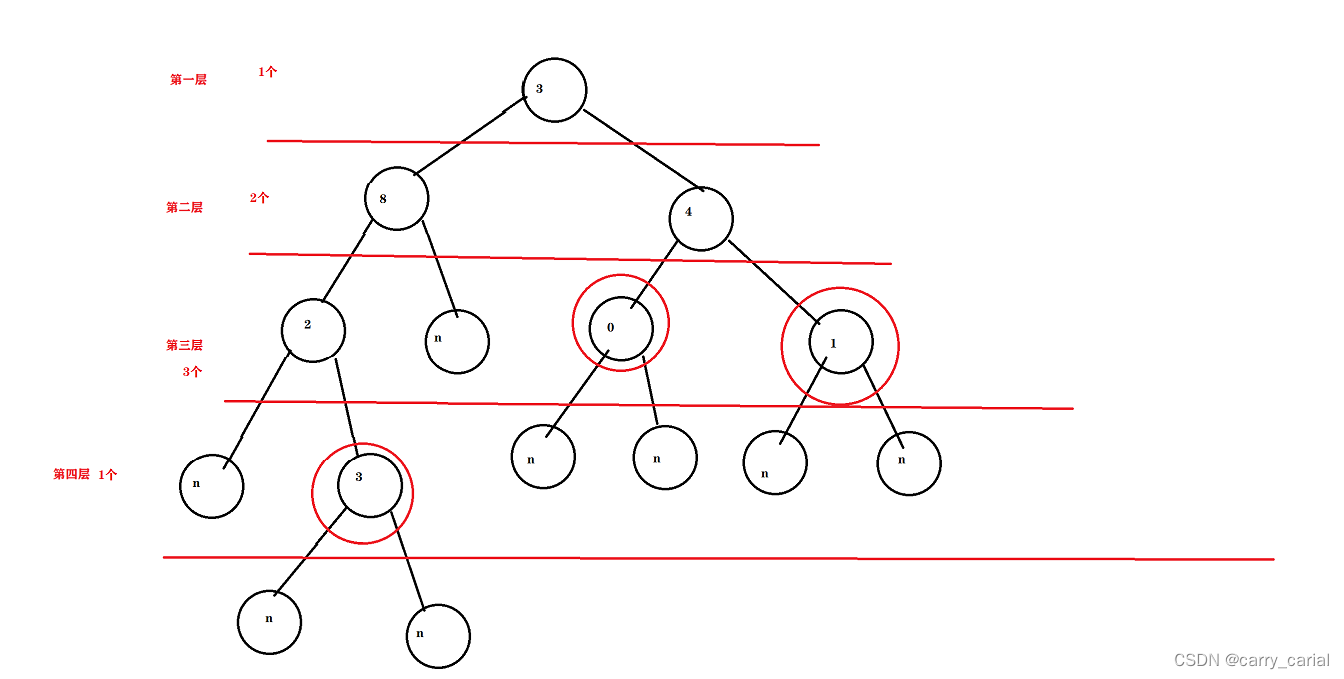
我们可以通过这个方法求解
当层数 > 1 的时候，层数不断向下走，直到层数 = 1，也就是找到本层
将本层的非 NULL 的节点个数进行返回

比如要找第三层，过程如下

程序

int countk(TreeNode* root , int k )
{
	if(root == NULL)
	{
		return 0;
	}
	if(k==1)
	{
		return 1;
	}
	return countk(root->left)+countk(root->right);
}

二叉树查找值为x 的节点

图解
先看根节点，根节点不是，就要向左子树查找
左子树没有找到，就要向右子树查找
把找到的节点返回

TreeNode* FindNode(TreeNode* root,int x)
{
	if(root == NULL)
	{
		return NULL;
	}
	if(root->val == x)
	{
		return root;
	}
	TreeNode* left = FindNode(root->left,x);
	TreeNOde* right = FindNode(root->right,x);

	return left == NULL ? right : left;
	
}