前言:
我们首先要明白什么是三路快排,什么是topk问题。
三路快排:
思想:
三路快排就是数组分3块,三个指针,先随机取一个基准值key,然后将数组划分为3个部分:
【小于key】【等于key】【大于key】
此时key的值的位置就确定了,然后再递归遍历小于key部分,和大于key的部分。
具体实现:根据nums[i]的值分类讨论

优化:用随机的方式选择基准元素
随机的实现就是先用srand函数种下一个种子,然后再调用rand函数。
原码:
class Solution {
public:
vector<int> sortArray(vector<int>& nums) {
//种下随机数种子
srand(time(NULL));
int left = 0;
int right = nums.size()-1;
qsort(nums,left,right);
return nums;
}
//随机生成比较元素key
int GetRandom(vector<int>& nums,int left,int right)
{
int r = rand();
int key = nums[r%(right-left+1) + left];//最后结果需要加上left
return key;
}
void qsort(vector<int>& nums,int l,int r)
{
if(l >= r) return;//判断条件写在第一行
int key = GetRandom(nums,l,r);
int i = l;
int left = l - 1;
int right = r + 1;
//一趟遍历,将key的值固定顺序
while(i < right)//注意循环遍历条件
{
if(nums[i] == key) i++;
else if(nums[i] > key)
{
swap(nums[i],nums[--right]);
}
else
{
swap(nums[i++],nums[++left]);
}
}
//递归调用
qsort(nums,l,left);
qsort(nums,right,r);
}
};第二个问题:什么是topk问题?
topk问题一般分为两大类:
第一大类就是找最大/最小的第k个元素,这一类只需要找一个元素即可。
第二大类就是最大/最小的k个元素,这一类是找一串数字。
在有上面的知识后,我们先解决第一类问题如何找第k个元素。
第一类问题:
215. 数组中的第K个最大元素
题目描述:
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
解法:
一般topk问题我们也是可以用堆排序区解决,但是这道题目的时间复杂度要求是O(N),而我们的堆排序的时间复杂度是N*LOGN,所以仍然是我们快速排序的主场!
我们的算法是建立在三路快排的思想上,我们根据已经将数组分为三部分的基础上,根据每一部分元素的数量与k进行比较来去确定具体在哪一个区间。

原码:
class Solution {
public:
//三路快排
int findKthLargest(vector<int>& nums, int k) {
int left = 0,right = nums.size()-1;
//随机数种子
srand(time(NULL));;
int ans = qsort(nums,left,right,k);
return ans;
}
int GetRandom(vector<int>& nums,int left,int right)
{
int r = rand();
//注意加上left
return nums[r%(right-left+1) + left];
}
int qsort(vector<int>& nums,int l,int r,int k)
{
//为什么不用考虑大于的情况,因为后续会判断
if(l == r) return nums[l];
int left = l - 1;
int right = r + 1;
int i = l;
//先将数组分为三块
int key = GetRandom(nums,l,r);
//因为是第k大,所以排降序
while(i < right)
{
if(nums[i] == key) i++;
else if(nums[i] < key) swap(nums[i++],nums[++left]);
else swap(nums[i],nums[--right]);
}
//分情况讨论,第k大元素具体在哪一段,直接return
int c = r - right + 1,b = right - left - 1;
if(c >= k) return qsort(nums,right,r,k);
else if(b + c >= k) return key;
else return qsort(nums,l,left,k-b-c);
}
};再解决第二类问题:
面试题 17.14. 最小K个数
题目描述:
设计一个算法,找出数组中最小的k个数。以任意顺序返回这k个数均可。
解法:
这一题跟上一题寻找第K个元素,思想基本一样,都是将寻找的区间缩小,本题返回值是一串数字,直接返回{nums.begin(), nums.begin()+k}即可
原码:
class Solution {
public:
//三路快排
vector<int> smallestK(vector<int>& arr, int k) {
srand(time(NULL));
int left = 0,right = arr.size()-1;
qsort(arr,left,right,k);
//注意返回值的书写方式
return {arr.begin(),arr.begin()+k};
}
int getRandom(vector<int>& arr,int left,int right)
{
int r = rand();
return arr[r%(right-left+1) + left];
}
void qsort(vector<int>& arr,int l,int r,int k)
{
if(l >= r) return;
int left = l - 1,right = r + 1;
int key = getRandom(arr,l,r);
int i = l;
while(i < right)//不能等于!
{
if(arr[i] == key) i++;
else if(arr[i] > key) swap(arr[i],arr[--right]);
else swap(arr[i++],arr[++left]);
}
//分情况讨论
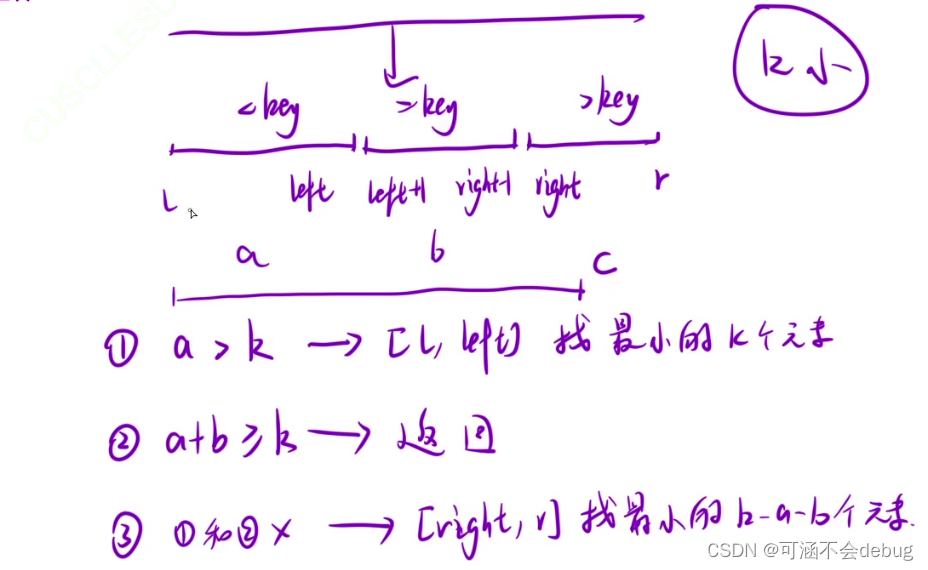
//[l,left] [left+1,right-1] [right,r]
int a = left - l + 1;
int b = right - left - 1;
if(k <= a) qsort(arr,l,left,k);
else if(k <= a+b) return;
else qsort(arr,right,r,k-a-b);
}
};