2024美国大学生数学建模C题网球运动中的势头详解思路+具体代码

E题数据已更新,做E题的小伙伴推荐看看博主的E题解析文章。那么废话不多说我们继续来做C题。
赛题分析
我们先阅题:
在2023年温布尔登男单决赛中,20岁的西班牙新星卡洛斯·阿尔卡拉兹击败了36岁的 诺瓦克·德约科维奇。这是德约科维奇自2013年以来在温布尔登的首次失利,也终结 了这位历史上最伟大的大满贯选手之一的辉煌战绩。
这场比赛本身就是一场非凡的战斗。[1]德约科维奇似乎注定要轻松获胜,因为他以6比1 控制了第一局(7局中赢了6局)。然而,第二盘比赛气氛紧张,最终阿尔卡雷斯在抢七局 中以7 - 6获胜。第三局与第一局相反,阿尔卡拉斯以6 - 1轻松获胜。这位年轻的西班 牙人在第四盘开始时似乎完全控制了比赛,但不知怎么的,比赛再次改变了方向,德约 科维奇完全控制了比赛,以6比3赢得了比赛。第五盘也是最后一盘,德约科维奇从第四 盘开始保持优势,但再次改变方向,阿尔卡拉兹获得控制并以6比4获胜。本次比赛的数 据在提供的数据集中,“match_id”为“2023-wimbledon1701”。你可以用“set_no” 列= 1看到德约科维奇在第一盘领先时的所有得分。令人难以置信的挥杆,有时是在许多 分甚至是比赛中,发生在似乎有优势的球员身上,通常被归因于“势头”。
读到这里感觉这个题有点意思,比较抽象。这美赛难道是想让我们建模找出势头?说实话这玩意多半是和时间序列预测有关,而且这东西预测出来有点虚无缥缈,也就是言之有理即可,重要的是有过程的数据分析,题目不会算很难,给了很多答主自由选择模型的空间。我们继续往下读题:
字典上对动量的一个定义是“通过运动或一系列事件获得的强度或力”。[2]在体育运 动中,一个团队或球员在比赛中可能会感到他们有动力,或“力量/力量”,但很难衡 量这种现象。此外,我们也不清楚比赛中的各种事件是如何创造或改变动量的。 2023年温布尔登男单前两轮之后的每一分数据。你可以选择包含额外的玩家信息或其他 数据,但你必须完整地记录这些来源。使用这些数据:
(1).开发一个模型,在游戏流程捕捉势头,并将其应用于一场或多场比赛。你的模型应该识别出哪名球员在比赛的特定时间表现更好,以及他们的表现有多好。 提供基于您的模型的可视化来描述匹配流。注:在网球比赛中,发球的选手赢得得 分/比赛的可能性要大得多。您可能希望以某种方式将此因素纳入您的模型中。
(2).一位网球教练怀疑“势头”在比赛中是否起作用。相反,他假设一个玩家在游戏中 的波动和成功的运行是随机的。使用你的模型/指标来评估这种说法。
(3).教练们很想知道,是否有一些指标可以帮助确定比赛流程何时会从有利于一名球员转变为有利于另一名球员。
- 使用至少一场比赛提供的数据,开发一个预测比赛中这些摆动的模型。哪些因素看起来最相关(如果有)?
- 考虑到过去比赛中动量波动的差异,你如何建议一个球员在新的比赛中面对不同的球员?
(4).在一个或多个其他比赛中测试你开发的模型。你对比赛结果的预测有多准确?如果模 型有时表现不佳,您能否确定可能需要包括在未来模型中的任何因素?您的模型对 其他比赛(如女子比赛)、锦标赛、球场表面和其他运动(如乒乓球)的通用性如何?
(5).提交一份不超过25页的调查报告,并包括一到两页的备忘录,总结你的结果,并就“ 势头”的作用向教练提出建议,以及如何让球员准备好应对影响网球比赛过程的事件。
题一、抓捕势头模型
不看数据集不知道,一看数据集单场比赛居然可以有这么多特征,那么该题的最大问题就是如何用好这些数据集了。首先我们要明白一点,就是这些数据是建立在时间之上的,也就是时序数据。时序数据不能用传统的数据分析方法,而是要尽可能将时间视为一个特征链去分析,也就是视为一个x轴,在时间轴上去衡量计算各个维度的特征关联。模型应该能够在比赛的任何给定时间点评估哪位选手表现更好,以及他们的表现优势有多大。此外,模型应该考虑到发球方赢得得分/局的概率通常更高这一因素。
单次比赛数据包含了详细的比赛信息,包括比赛ID、选手姓名、比赛经过的时间、盘数、局数、分数等多达46个字段。这些数据提供了每一分的详细记录,包括选手的得分情况、发球速度、发球方向、球的落点深度、选手跑动距离、连续击球数(rally count)等。
数据处理和分析
首先,需要整理和分析提供的数据。这可能包括每个得分的详细信息,比如哪位选手得分、得分是如何获得的(例如,发球得分、主动得分或对手失误)以及得分时的比赛状态(例如,比分、局数、盘数)。
附加数据:可能还需要考虑选手的一些基本信息,如世界排名、赛前状态、历史对决记录等,这些都可能影响比赛动力的评估。
我们需要详细分析每个得分事件,并根据比赛情况(如谁赢得了分数)来更新得分,所以进行积分规则编程尤为重要。
建模思路
- 解析规则:根据提供的计分规则,我们需要一个函数来解释每个得分事件,并更新每位选手的得分。
- 计算得分:我们将使用比赛的得分事件来模拟每个游戏内的得分变化。每位选手的得分将根据比赛规则更新。
- 确定动力:我们可以通过考虑比赛中的关键事件(如破发点、保发、发球优势)来确定每位选手的动力。动力可以用得分差异来表示,也可以通过其他衡量方式来衡量,比如连续得分或突然得分变化。
- 可视化:使用得分差异和比赛关键时刻,我们可以创建一个时间序列图来显示比赛动力的变化。
规则题目已经给出:

那么我们开始进行仿真模拟单场发球规则,而且这么多维度的数据,必须要进行降维或者是优化得分更新逻辑,或者将数据分批处理,在更新得分之前先预处理数据以减少需要处理的数据量。
由于网球比赛的计分规则相对复杂,我们需要确保模型能够处理以下情况:
- 普通得分,从0(Love)开始,到15、30、40,然后赢得游戏。
- 当双方得分都达到40(Deuce)时,需要赢得连续两分才能赢得游戏。
- 盘的胜利需要赢得至少6个游戏,并且至少领先对手2个游戏。如果双方都赢得6个游戏,那么进行决胜局。
- 比赛的胜利需要赢得3个盘。
在网球得分系统中,当比分到达40-40(Deuce)时,需要连续赢得两分才能赢得该游戏。此外,在6-6平局时,通常会进行决胜局(Tie-break),其计分规则与普通游戏不同。在决胜局中,首先赢得7分(必须领先2分)的选手将赢得该盘。如果是比赛的最后一盘(通常是第五盘),则可能需要10分来赢得胜利。所以我们还需要加入Deuce规则:
考虑以上40-40(Deuce)的情况:
| Row | column(s) | Value(s) | Description |
|---|---|---|---|
| Row 8 | p1_score, p2_score | 40, 40 | The score is 40 – 40 meaning each player has won 3 previous points (this is also called “deuce”) |
| point_victor | 1 | Alcaraz wins point 7 (in row 8) | |
| Row 9 | p1_score, p2_score | AD,40 | Since Alcaraz won the previous point (point 7) the score on point 8 is now “AD” for Alcaraz and “40” for Jarry meaning Alcaraz has won one more point and could win the game on the next point. |
| point_victor | 2 | Jarry (player 2) wins point 8 (in row 9). | |
| Row 10 | p1_score, p2_score | 40, 40 | The score returns to 40 – 40 (“deuce”) meaning each player has won the same number of previous points although now it is 4 points each. |
| point_victor | 1 | Alcaraz wins point 9 (in row 10). | |
| Row 11 | p1_score, p2_score | AD,40 | Alcaraz again has the advantage having won point 9 |
| point_victor | 1 | Alcaraz wins point 10 (in row 11) which means he has won the game (has score 2 more points now). | |
| Row 12 | game_no | 2 | This is now the first point of game 2. |
| p1_games | 1 | Alcaraz won game 1. |
# 定义更新得分的函数,考虑到deuce和advantage的情况
def update_match_scores(df):
p1_points, p2_points = 0, 0 # Points in a game
p1_games, p2_games = 0, 0 # Games in a set
p1_sets, p2_sets = 0, 0 # Sets in the match
for index, row in df.iterrows():
if row['point_victor'] == 1:
p1_points += 1
else:
p2_points += 1
if p1_points >= 4 and p1_points - p2_points >= 2:
p1_games += 1
p1_points, p2_points = 0, 0 # Reset points
elif p2_points >= 4 and p2_points - p1_points >= 2:
p2_games += 1
p1_points, p2_points = 0, 0 # Reset points
if p1_games >= 6 and p1_games - p2_games >= 2:
p1_sets += 1
p1_games, p2_games = 0, 0 # Reset games
elif p2_games >= 6 and p2_games - p1_games >= 2:
p2_sets += 1
p1_games, p2_games = 0, 0 # Reset games
df.loc[index, 'p1_points'] = p1_points
df.loc[index, 'p2_points'] = p2_points
df.loc[index, 'p1_games'] = p1_games
df.loc[index, 'p2_games'] = p2_games
df.loc[index, 'p1_sets'] = p1_sets
df.loc[index, 'p2_sets'] = p2_sets
return df
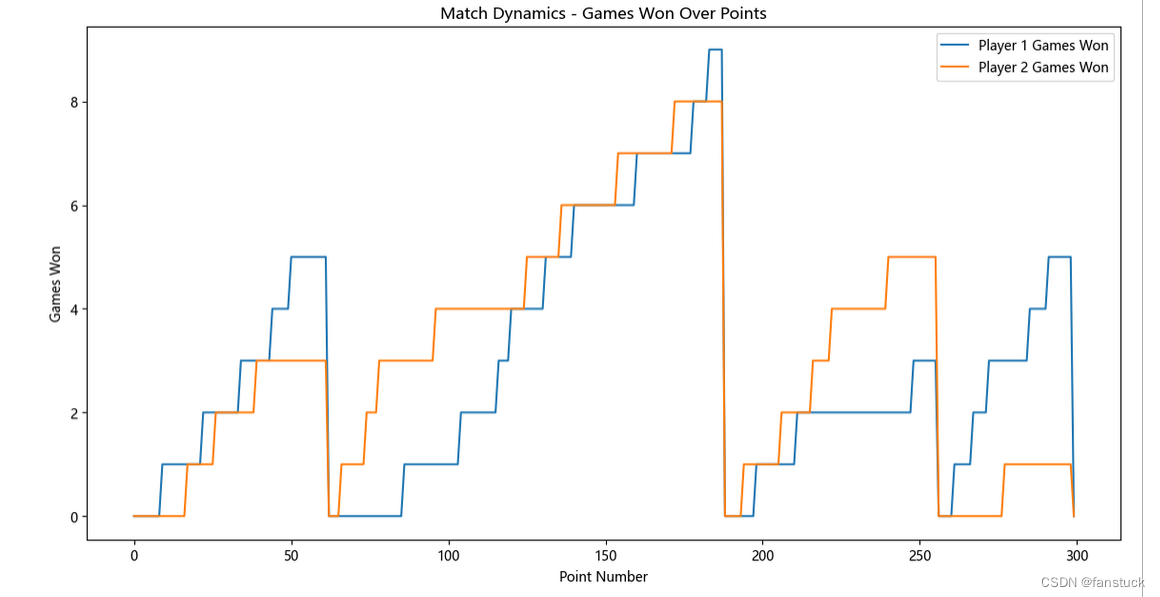
这样一来我们就先完成了捕捉赛点发生时的比赛流程模拟,现在捕捉势头也就是预测峰值走向,其实就是梯度的概念,下一步我们开始进行时序预测模型的建模处理:

这样一来我们就先完成了捕捉赛点发生时的比赛流程模拟,现在捕捉势头也就是预测峰值走向,其实就是梯度的概念,下一步我们开始进行时序预测模型的建模处理。
对时序预测算法不是很有把握的推荐去看看博主之前写的专栏,很有帮助。先记录到这里后面整理一下,期待大家的关注和支持!就是我一直以来写作的动力!