目录

题目描述

输入描述

输出描述

用例

题目解析

算法源码

---

题目描述

有一个考古学家发现一个石碑，但是很可惜，发现时其已经断成多段，原地发现n个断口整齐的石碑碎片。为了破解石碑内容，考古学家希望有程序能帮忙计算复原后的石碑文字组合数，你能帮忙吗？

输入描述

第一行输入n，n表示石碑碎片的个数。

第二行依次输入石碑碎片上的文字内容s，共有n组。 

输出描述

输出石碑文字的组合（按照升序排列），行末无多余空格。

用例

输入	3 a b c
输出	abc acb bac bca cab cba
说明	无

输入	3 a b a
输出	aab aba baa
说明	无

题目解析

本题其实就是LeetCode - 47 全排列 II_伏城之外的博客-CSDN博客

上面这篇博客提供了一种去重计数后求全排列的方案。

这里我介绍另一种方案，即树层去重。

如果我们将输入的数组进行排序，比如 [a,b,a] 升序后为 [a,a,b]

那么此时求全排列，必然会有如下过程：

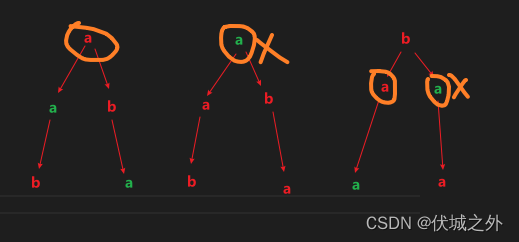
 我们发现，第二颗树和第一颗树完全重复，第三颗树的第二层的两个分支重复。

因此，按照本题要求，我们需要将上面两处重复去除。

其实这就是树层去重。

即全排列树的某一层兄弟节点重复了，则其以下分支必然重复。

因此，我们需要判断，如果全排列树的某一层兄弟节点发生重复，则不进行后续树枝生成。

那么如何判断同一层兄弟节点呢？

dfs的for循环中的操作就是当前树层的操作，而for循环中的递归dfs调用就是对下一树层的操作。

因此，我们判断当前树层的节点是否何其同一层的兄弟节点重复，即判断arr[i] === arr[i-1]

但是这种方式，不仅会判断同一树层的兄弟节点，还会判断相邻树层的父子节点，如下图所示

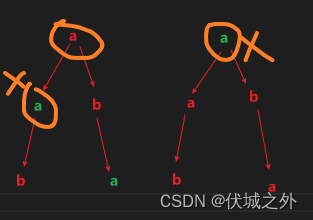
因此，为了只对树层进行操作，我们需要增加一个过滤条件：

树枝父节点arr[i-1] 的 used[i-1] 是使用过的

而树层兄弟节点arr[i-1] 的 used[i-1]是未使用的 

 因此，最终判断如下

 

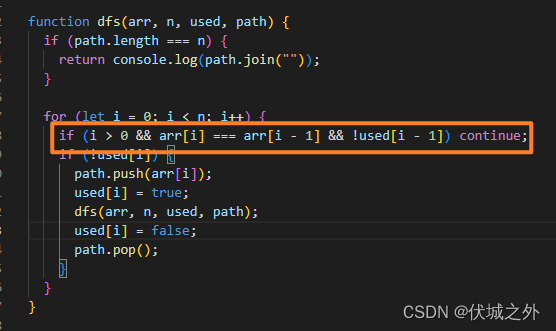
算法源码

/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");

const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

const lines = [];
rl.on("line", (line) => {
  lines.push(line);

  if (lines.length === 2) {
    const n = parseInt(lines[0]);
    const arr = lines[1].split(" ").sort();

    dfs(arr, n, new Array(n).fill(false), []);
    lines.length = 0;
  }
});

function dfs(arr, n, used, path) {
  if (path.length === n) {
    return console.log(path.join(""));
  }

  for (let i = 0; i < n; i++) {
    if (i > 0 && arr[i] === arr[i - 1] && !used[i - 1]) continue;
    if (!used[i]) {
      path.push(arr[i]);
      used[i] = true;
      dfs(arr, n, used, path);
      used[i] = false;
      path.pop();
    }
  }
}