Pytorch的grid_sample是如何实现对grid求导的？（源码解读）

这里本人的参考源码是grid_sample的CPU内核的CPP实现：https://github.com/pytorch/pytorch/blob/b039a715ce4e9cca82ae3bf72cb84652957b2844/aten/src/ATen/native/cpu/GridSamplerKernel.cpp。

grid_sample功能简述

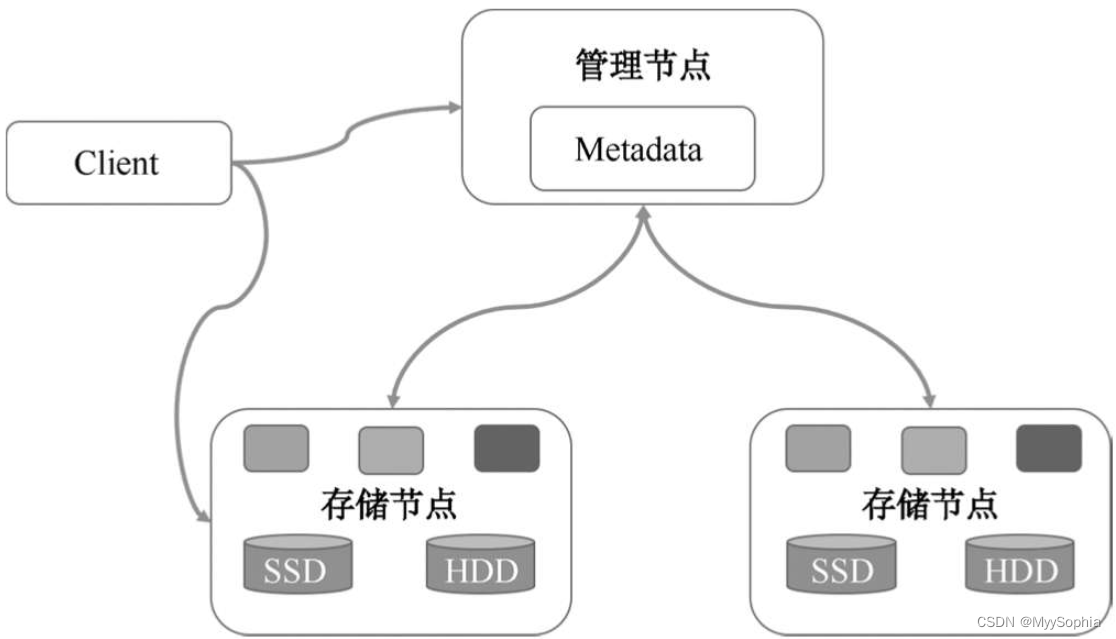
给定一个input（4D或5D，一般指原图像）和一个流场grid（4D或5D，一般指变形流），基于来自grid的像素位置和input的像素值计算output（输出图像）。
例如，对于4D的情况，input的形状为(N,C,H_in,W_in)，grid的形状为(N,H_out,W_out,2)，那么输出结果即为(N,C,H_out,W_out)。对于output的每个位置(i, j)，将根据grid在(i, j)上的值(x, y)，从input的(x, y)处采样像素值（采样过程要考虑x、y非整值和越界的情况），用作output在(i, j)处的像素值。
（grid的值应当是根据input的空间维度(H,W)归一化到[-1,1]后的像素点坐标。例如x=-1，y=1代表输入的左上角像素。）
如果grid具有超出[-1,1]范围的值，相应的输出由padding_mode来处理：

1. padding_mode=“zeros”：超出范围的grid值用0替代。
2. padding_mode=“border”：超出范围的grid值用边界值替代。
3. padding_mode=“reflection”：超出范围的grid值用通过边界反射后的值替代。

基本流程

• 定义结构体“ComputeLocation”：作用是基于padding模式计算插入位置
• 定义结构体“ApplyGridSample”：作用有两个：（1）提供N（即空间维度）个“ComputeLocation”结构体，然后利用他们去计算对应维度的插入位置；（2）插入值并且写入到output。
• 定义方法“grid_sample_2d_grid_slice_iterator”函数：作用有两个：（1）迭代grid张量的每一个值即(x,y)对；（2）在每次迭代时应用一个给定的操作器（可以视为是上述的ApplyGridSample中前向和反向传播方法），使得在前向和反向传播时可以使用相同的模式。

实现细节

• “ComputeLocation”结构体
  apply()函数：输入grid值in，返回去标准化和应用padding机制（逐像素）后的插入位置
  apply_get_grad()函数：输入grid值in，类似于apply，但也会返回apply(in)关于in的偏导数（返回值是一个vec对）（逐像素），通常用于梯度计算中。（这里并没有计算全部的梯度，仅仅是算了根据grid获得去标准化后插入坐标这个过程所得到的梯度）
  比如说，采用zeros填充的实现如下：
  
  这里的apply_get_grad()函数就仅仅对输入grid做了一个去归一化（本质上是通过(in+1)*half_max_val实现的，in的大部分值应位于[-1,1]范围内）作为输出，因此对应的偏导数仅仅就是half_max_val。
• 对于padding=“zeros”：返回的插入位置值未必全部落在[0, w]和[0,h]范围内，偏导为half_max_val。
• 对于padding=“border”：返回的插入位置值必定全部落在[0,w]和[0,h]范围内，偏导对于原始grid输入in落在[-1,1]范围上的值为half_max_val，否则为0。
• 对于padding=“reflection”：返回的插入位置值必定落在[0,w]和[0,h]范围内，偏导求法可以自己看看。

2. “ApplyGridSample”结构体
   具有N个“ComputeLocation”结构体，其中N是空间维度的数量（对于二维图像H*W，N即为2）。给定N个输入grid向量（每个空间维度一个）和空间偏移，其从“ComputeLocation”中获得对应的插入位置，应用插入过程，并将结果写入输出（对于反向传播过程即是写入grad_input和grad_grid）
   forward()函数：应用网格采样（前向）过程（上述），输出out_slice
   backward()函数：应用反向传播过程，参数与机制和前向过程类似，输出grad_input，grad_grid
   比如说，采用双线性插值的forward()函数实现如下：

inline void forward(TensorAccessor<scalar_t, 3>& out_slice,
                      const TensorAccessor<scalar_t, 3>& inp_slice,
                      int64_t offset, const Vec& grid_x, const Vec& grid_y,
                      int64_t len) const {
    auto x = compute_W.apply(grid_x);
    auto y = compute_H.apply(grid_y);	// 首先根据grid算出反归一化后的插入位置

	//基于双线性插值，对每个位置（小数）首先获得四个方向（到最近的整数位置）上的距离作为插值的权重
	//会返回权重和mask（考虑是否需要处理超出边界的部分）
    auto interp_params = compute_interp_params(x, y); 

	//以下皆为上一个函数的返回值
    auto nw = std::get<4>(interp_params);
    auto ne = std::get<5>(interp_params);
    auto sw = std::get<6>(interp_params);
    auto se = std::get<7>(interp_params);

    auto nw_mask = std::get<8>(interp_params);
    auto ne_mask = std::get<9>(interp_params);
    auto sw_mask = std::get<10>(interp_params);
    auto se_mask = std::get<11>(interp_params);

    auto i_y_n = std::get<12>(interp_params);
    auto i_x_w = std::get<13>(interp_params);
	
	//获得原图input上grid所指示的位置附近四个整数像素点的位置
    auto i_nw_offset = i_y_n * iVec(inp_sH) + i_x_w * iVec(inp_sW);
    auto i_ne_offset = i_nw_offset + iVec(inp_sW);
    auto i_sw_offset = i_nw_offset + iVec(inp_sH);
    auto i_se_offset = i_sw_offset + iVec(inp_sW);

    #ifndef _MSC_VER  
    # pragma unroll  
    #endif
    for (int64_t c = 0; c < C; ++c) {	//C为batch_size
      auto inp_slice_C_ptr = inp_slice[c].data();

      // mask_gather zeros out the mask, so we need to make copies
      Vec nw_mask_copy = nw_mask;
      Vec ne_mask_copy = ne_mask;
      Vec sw_mask_copy = sw_mask;
      Vec se_mask_copy = se_mask;
      //获得原图中四个方向位置中的像素值
      //这里其实是通过对输入图像的底层指针进行偏移量计算来实现根据索引进行插入的效果的
      auto nw_val = mask_gather<sizeof(scalar_t)>(Vec(0), inp_slice_C_ptr, i_nw_offset, nw_mask_copy);
      auto ne_val = mask_gather<sizeof(scalar_t)>(Vec(0), inp_slice_C_ptr, i_ne_offset, ne_mask_copy);
      auto sw_val = mask_gather<sizeof(scalar_t)>(Vec(0), inp_slice_C_ptr, i_sw_offset, sw_mask_copy);
      auto se_val = mask_gather<sizeof(scalar_t)>(Vec(0), inp_slice_C_ptr, i_se_offset, se_mask_copy);
	  //根据各方向权重计算出最终插值结果
      auto interpolated = (nw_val * nw) + (ne_val * ne) + (sw_val * sw) + (se_val * se);
      interpolated.store(out_slice[c].data() + offset, len);
    }

backward()计算关于grid的梯度关键：

gx = gx + ((ne_val - nw_val) * s + (se_val - sw_val) * n) * gOut;
gy = gy + ((sw_val - nw_val) * e + (se_val - ne_val) * w) * gOut;

这里gOut应指来自下一层传回的梯度，ne_val，nw_val，se_val，sw_val指四个方向位置上的原图像像素值，这四个值都是通过以grid值作为索引查找原图像相邻位置去获取到的；s、n、e、w分别指该grid值到这四个方向整数位置上的一个距离（用作双线性插值的权重）。
3. “grid_sample_2d_grid_slice_iterator”函数
提供一个抽象来有效地迭代一个“grid”分片（不带batch维度）。实质上是遍历了每个实例，然后对每个实例应用上述前向和反向处理。

总结

（在双线性插值下），grid_sample()对grid求导采取了类似图像梯度的方式，直接用每个grid值关联到的周围四个位置上的像素值，将两两的差值乘上一个权重（双线性插值的距离），用作本函数的梯度，然后传回给前一层。

思考

考虑这么一个图像矫正的问题，如果有一张输入的变形图像inp，一个参考恢复网格grid_gt，一个预测恢复网格grid_pred，要衡量grid_pred网格的正确性，有两种做法：

• 直接计算grid_pred和grid_gt的距离（比如说L1距离），作为衡量grid_pred的指标。
• 分别使用grid_pred和grid_gt对原图像inp应用grid_sample()函数，将矫正结果的距离用作衡量grid_pred的指标。

由于任务关心的实际上是最终的矫正结果的效果，而不是grid绝对值的差距，因此本人认为后一种方法更加准确。再结合上述对grid_sample()求导的分析，这两种方法传递的梯度信息是大不相同的（也即后一种做法在实现上是具有意义的），grid_sample()对grid某点值的偏导会考虑该点在原图像上所有相邻点的像素值。

由于本人水平有限，对代码的理解上可能不够深入，如果存在错误之处，请大神在评论区指正！