C++(17）——list的模拟实现

前面的文章中，介绍了 $string$ ， $vector$ 的模拟实现，本篇文章将介绍对于 $list$ 的模拟实现。

1. list的基本结构：

2. list功能实现：尾部插入元素：

3. list迭代器的实现：

4. list功能实现：在任意位置前插入元素：

4.1 函数实现方法：

4.2 函数运行逻辑：

5. list功能实现：删除任意位置的结点：

6. 拷贝构造与赋值重载：

7. list功能实现：clear与析构函数：

1. list的基本结构：

对于 $list$ ，可以将其看作数据结构中的双向带头循环链表一起学数据结构（4）——带头结点的双向循环链表_带头结点的双循环链表-CSDN博客

针对于双向带头循环链表，其基本构成单元为如下图所示：

其中， $prev$ 用来保存上一个结点的地址， $next$ 用于保存下一个结点的地址， $data$ 用于保存数据。对于上述结构单元，可以由下方的代码表示：

namespace violent
{
	template<class T>
	struct ListNode
	{
		ListNode<T>* _prev;
		ListNode<T>* _next;
		T _data;
	};
}

对于双向带头循环链表，其结构可以由下图表示：

其中，链表的第一个结点称为哨兵位头结点，此结点的 $data$ 不用于存储数据，只是利用 $prev,next$ 建立其他结点的关系。因此，在编写针对于链表单元结构的构造函数时，需要考虑到哨兵位头结点。本文将采用隐式类型转换的方式，来完成对于构造函数的编写：

template<class T>
	struct ListNode
	{
		ListNode(const T& x = T())
			: _prev(nullptr)
			, _next(nullptr)
			, _data(x)
		{}
		
		ListNode<T>* _prev;
		ListNode<T>* _next;
		T _data;
	};

对于一个带头双向循环链表结构的实现，可以看作是若干个结构单元的相互链接，因此在初始化链表结构时，只需要在构造函数中，完成对于哨兵位头结点的建立，以及其内部指针的指向即可，即：

具体的实现方法，就是再创建一个类，名为 $list$ 的类，将上述表示单个结点结构的类作为一种类型引入到 $list$ ，即：

template<class T>
	class list
	{
		typedef ListNode<T>  Node;
		Node* _node;
	};

通过上述给出的图片，可以得到下面的构造函数：

class list
	{
		typedef ListNode<T>  Node;
	public:
		list()
		{
			_phead = new Node;
			_phead->_next = _phead;
			_phead->_prev = _phead;
		}
		Node* _phead;
	};

2. list功能实现：尾部插入元素：

在插入一个元素之前，首先需要创建一个新的结构单元用于保存这个元素，例如需要插入的元素为 $x$ ，需要提前创建一个名为 $newnode$ 的结点用于存储该元素，即：

Node* newnode = new Node(x);

当 $newnode$ 进行插入时，即：

第一步，首先获取链表最后一个结点的地址，这里命名为 $tail$ ，通过上图不难得出 $taii=phead->prev$ .

第二步，建立 $newnode$ 与 $tail$ 的联系，即： $tail->next=newnode$ , $newnode->prev=tail$ ，对于此关系的图片表示是如下：

最后一步：建立 $phead$ 与 $newnode$ 的联系，即 $phead->prev=newnode$ , $newnode->next=phead$

代码实现如下：

void push_back(const T& x)
		{
			Node* newnode = new Node(x);
			Node* tail = _phead->_prev;
			tail->_next = newnode;
			newnode->_prev = tail;
			newnode->_next = _phead;
			_phead->_prev = newnode;
		}

3. list迭代器的实现：

在 $vecotr,string$ 中，由于这两种数据结构的空间是连续的，因此，在实现其迭代器功能时，通常先利用 $typedef$ 对指针进行更名，使用时直接 $++$ 即可。

但是对于 $list$ ，前面说到 $list$ 的结构可以近似的看为链表，由于链表的空间不连续，因此，在使用迭代器进行访问时，对迭代器 $++$ 不能达成访问空间中下一个结点的目的。对于 $list$ 来说，正确访问下一个结点的访问为通过本结点的 $next$ 获取下一个结点的地址。因此，可以考虑使用运算符重载，将 $++$ 的运行逻辑从指向连续空间的下一个地址改为通过本结点的 $next$ 访问下一个结点。

但是，运算符重载只能针对于自定义类型，因为迭代器的实现是依托于指针来完成的。虽然在前面利用创建自定义类型的方式创建了链表中单个结点结构的对象，但是，需要注意，此处运算符重载进行重载的目标并不是 $ListNode$ 这个自定义类型，而是这个类型的指针，而指针是一个内置类型，因此，不能直接完成对于指针的重载。而是再创建一个自定义类型用于封装指针，在内部进行运算符重载。

对于封装方法：首先需要将表示单个结点结构的自定义类型引入到新的类中，此处将这个类命名为__ $list$ _ $iterator$ 。为了方便使用，将表示单个结点结构的类重命名为 $Node$ ，成员变量为类型为 $Node$ 的指针。即：

template<class T>
		struct __list_iterator
		{
			typedef ListNode<T> Node;

			Node* _node;
		};

对于上述类的初始化如下：

template<class T>
		struct __list_iterator
		{
			typedef ListNode<T> Node;
			__list_iterator(Node* node)
				: _node(node)
			{}

			Node* _node;
		};

为了正常的使用迭代器来完成对于 $list$ 的打印，不但需要对于 $++$ ，还需要对于 $*$ 和 $!=$ 进行重载，代码如下：

template<class T>
	struct __list_iterator
	{
		typedef ListNode<T> Node;
		typedef __list_iterator<T> self;
		__list_iterator(Node* node)
			: _node(node)
		{}

		self& operator++()
		{
			_node = _node->_next;
			return *this;
		}

		self& operator++(int)
		{
			self tmp(_node);
			_node = _node->next;
			return tmp;
		}

		T& operator*()
		{
			return _node->_data;
		}

		bool operator!=(const self& s)
		{
			return _node != s._node;
		}

		Node* _node;
	};

在完成上述步骤后，向 $list$ 中引入__ $list$ _ $iterator$ ，再添加 $end,begin$ 两个函数用于表示链表的起始和结束。

需要注意的是，在定义链表的起始时，并不能定义成哨兵位头结点，因为哨兵位头结点并没有保存数据，在访问链表时，需要从第一个保存数据的结点开始访问。而对于尾结点，由于链表是双向循环的。因此，可以将不存储任意数据的哨兵位头结点看作尾结点，代码如下：

typedef __list_iterator<T> iterator;

		iterator begin()
		{
			return _phead->_next;
		}

		iterator end()
		{
			return _phead;
		}

在完成了上述步骤后，就可以使用迭代器对于 $list$ 进行正常的访问，例如：

void test1()
	{
		list<int> It;
		It.push_back(1);
		It.push_back(2);
		It.push_back(3);
		It.push_back(4);
		list<int>::iterator it1 = It.begin();
		while (it1 != It.end())
		{
			cout << *it1 << ' ';
			++it1;
		}
	}

代码运行结果如下：

4. list功能实现：在任意位置前插入元素：

4.1 函数实现方法：

与尾部插入元素的大致思路相同，首先需要创建一个结点来存储这个元素：

Node* newnode = new Node(x);

例如，需要在 $pos$ 位置之前插入这个结点，首先需要获取 $pos$ 位置的前一个结点的地址 $prev$ 。但是， $pos$ 只是类型为 $iterator$ 的一个对象，需要先创建一个变量 $cur$ ，来存储 $pos$ 中成员变量 $node$ ，也就是这个结点的地址，通过 $cur$ 来获取 $pos$ 位置前一个结点的坐标，即：

Node* cur = pos._node;

Node* prev = cur->_prev;

在对 $prev,newnode,cur$ 这三个位置所代表的结点进行连接，即：

void insert(iterator pos,const T& x)
		{
			Node* cur = pos._node;
			Node* prev = cur->_prev;
			Node* newnode = new Node(x);

			prev->_next = newnode;
			newnode->_prev = prev;
			newnode->_next = cur;
			cur->_prev = newnode;
		}

利用下方的代码对于 $insert$ 函数功能进行测试，即：

It.insert(It.begin(), 5);
		It.insert(It.begin(), 6);
		It.insert(It.begin(), 7);
		It.insert(It.begin(), 8);
		
		for (auto e : It)
		{
			cout << e << ' ';
		}

运行结果如下：

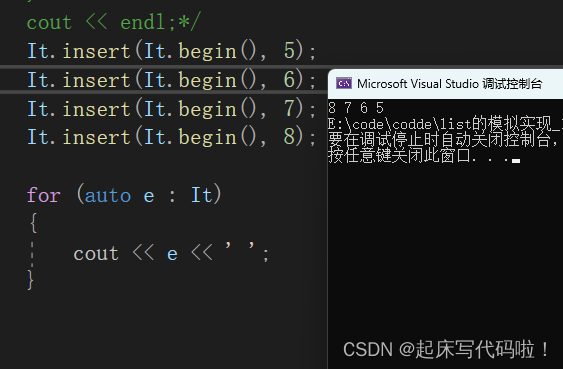
4.2 函数运行逻辑：

为了更清晰的了解 $insert$ 的动作逻辑，下面给出函数的整体运行步骤，例如对于下方的代码：

It.insert(It.begin(), 5);

函数运行的第一步为首先通过 $begin()$ 函数获取地址：

在返回时，由于函数的返回类型为自定义类型 $iterator$ ，因此在返回前会去调用__ $list$ _ $insert$ $iterator$ 中的构造函数，来构造一个临时变量作为返回值，即：

再获取返回值后，跳转到 $insert$ 函数中，即：

最后根据 $insert$ 中编写好的代码的顺序进行运行。

在完成了对于 $insert$ 函数的编写后，对于 $push$ _ $back$ 函数可以复用 $insert$ ，从而简化 $push$ _ $back$ ，即：

void push_back(const T& x)
		{
			insert(_phead, x);
		}

同理也可以实现头部插入任意元素 $push$ _ $front$ ，即：

void push_front(const T& x)
		{
			insert(_phead->_next, x);
		}

5. list功能实现：删除任意位置的结点：

在删除任意位置的结点前，首先需要找到这个结点的前结点和后结点的地址，为了方便表达，用 $prev$ 表示前结点的地址，用 $next$ 表示后结点的地址。代码如下：

iterator erase(iterator pos)
		{
			assert(pos != end());
			Node* cur = pos._node;
			Node* prev = cur->_prev;
			Node* next = cur->_next;

			prev->_next = next;
			next->_prev = prev;

			delete cur;
			return next;
		}

在完成了对于 $erase$ 的编写后，可以通过复用 $erase$ 来完成对于头部删除 $pop$ _ $front$ 和尾部删除 $pop$ _ $back$ ，代码如下：

void pop_back()
		{
			erase(_phead->_prev);
		}

		void pop_front()
		{
			erase(_phead->_next);
		}

利用下方代码对上述的函数进行测试：

It.pop_back();
		It.pop_back();
		It.pop_front();
		It.pop_front();
		for (auto e : It)
		{
			cout << e << ' ';
		}

运行结果如下：

6. 拷贝构造与赋值重载：

list(const list<T>& s)
		{
			empty();
			for (auto e : s)
			{
				push_back(e);
			}
		}

		void swap(list<T>& s)
		{
			std::swap(_phead, s._phead);
		}

		list<T>& operator=(list<T> s)
		{
			swap(s);
			return *this;
		}

7. list功能实现：clear与析构函数：

对于 $clear$ 函数，其功能是用于清理空间中的所有内容，即所有开辟的结点，但是不包括哨兵位头结点。

对于析构函数，则是在 $clear$ 函数的基础上，将哨兵位头结点也进行处理。

二者对应代码如下：

void clear()
		{
			iterator i2 = begin();
			while (i2 != end())
			{
				i2 = erase(i2);
			}
		}

		~list()
		{
			clear();

			delete _phead;
			phead = nullptr;
		}