在工程管理、经济管理、科学研究、军事作战训练及日常生产生活等众多领域中,人们常常会遇到各种优化问题。例如,在生产经营中,我们总是希望制定最优的生产计划,充分利用已有的人力、物力资源,获得最大的经济效益;在运输问题中,我们总是希望设计最优的运输方案,在完成运输任务的前提下,力求运输成本最小等。针对优化问题的数学建模也是数学建模竞赛中一类比较常见的问题,这样的问题常常可以使用数学规划模型进行研究。
数学规划是运筹学的一个重要分支,而线性规划又是数学规划中一部分主要内容。很多实际问题都可以归结为“线性规划”问题。线性规划(Linear Programming,LP)有比较完善的理论基础和有效的求解方法,在实际问题中有极其广泛的应用。
一句话:在什么限制(约束)下变量取什么值可以让的目标最优。
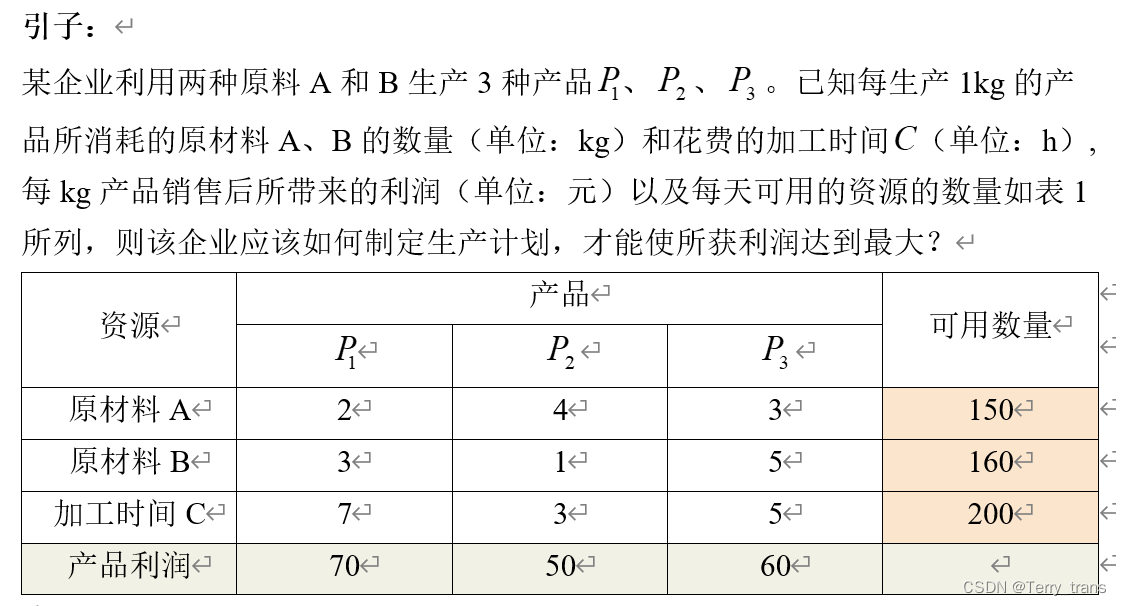
分析:
- 求什么?3种产品的产量 – 决策变量
- 考虑什么条件?原来料不能用光 and 总加工时间得够用 – 约束条件
- 达到什么目标?使得利润最大 – 目标函数

产品的产量应收到某些条件的限制。首先,两种原材料每天的实际消耗量不能超过其可用数量,因此有
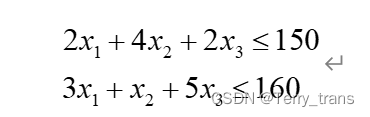

步骤:
- 分析问题,找出决策变量
- 根据问题给出的条件,找出决策变量必须满足的一组线性等式或者不等式约束,即为约束条件。
- 根据问题的目标,构造关于决策变量的一个线性函数,即为目标函数。
有了决策变量、约束条件和目标函数这3个要素之后,一个线性规划模型就建立起来了。

求解:
使用Gurobi求解器, Why Gurobi? 还是那句话:专业的事情专业的干

# 1.Gurobi版本
profit = [70, 50, 60] # 各产品恒单位利润
MatA = [2, 4, 3] # 各产品单位消耗的A原材料
MatB = [3, 1, 5] # 各产品单位消耗的B原材料
time = [7, 3, 5] # 各产品单位生产时间
resA = 150 # A原材料每天可用量
resB = 160 # B原材料每天可用量
available_time = 200 # 每天可用生产时间
from gurobipy import *
m = Model("maximize_profit") # 给模型起个名字
# 变量
x = m.addVars(3, vtype=GRB.CONTINUOUS, name="x")
# 目标
m.setObjective(sum(profit[i]*x[i] for i in range(3)), GRB.MAXIMIZE)
# 约束
m.addConstr(sum(MatA[i]*x[i] for i in range(3)) <= resA, "c0")
m.addConstr(sum(MatB[i]*x[i] for i in range(3)) <= resB, "c1")
m.addConstr(sum(time[i]*x[i] for i in range(3)) <= available_time, "c2")
m.optimize()
print("-----------------------------------------------------------------")
print("最大化利润为: ", m.objVal, "元")
# 检查模型是否存在最优解
if m.status == GRB.OPTIMAL:
# 输出每种产品的生产数量
for i in range(3):
print(f'产品{i+1} 生产数量: {x[i].x} 公斤')
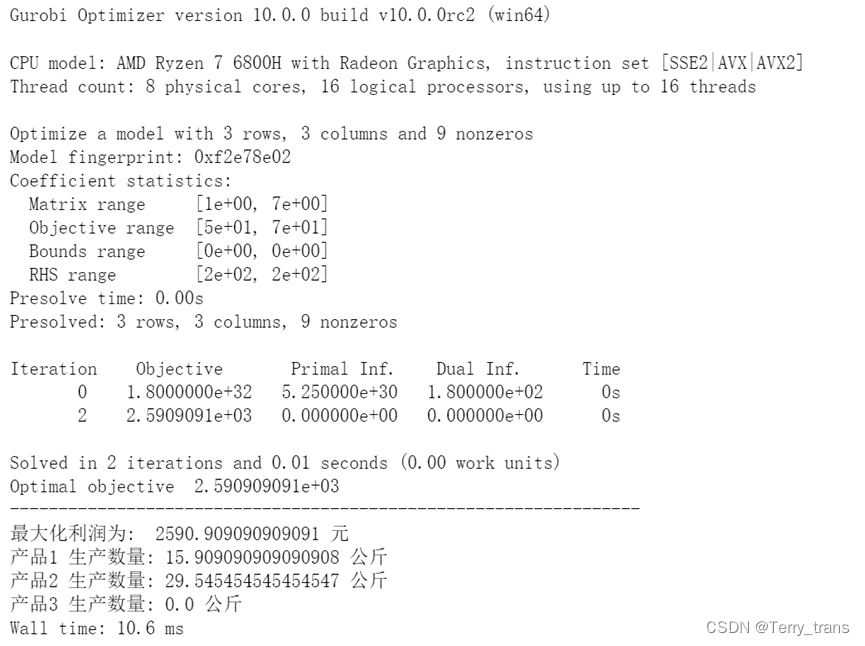
根据结果答:生产A产品15.90公斤,B产品29.54公斤,不生产C产品时利润最大2590.90元
注:如果大家安装Gurobi失败,可以先用python的pulp库做替代。
PuLP 是一个开源的 Python 语言线性规划建模库。它提供了构建线性规划(LP)、整数规划(IP)以及混合整数规划(MIP)模型的能力。PuLP 不自带求解器,而是作为一个接口层,可以与多个第三方求解器结合使用,包括但不限于 COIN-OR 的 CBC、GLPK、Gurobi、CPLEX 等。用户可以通过 PuLP 定义变量、约束条件和目标函数,并选择合适的求解器来解决问题。Pulp默认的求解器是CBC。
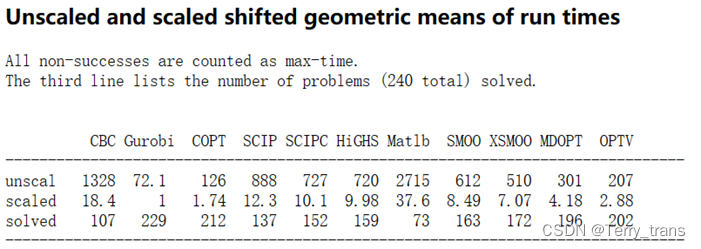
在全球最著名的专业优化器评比网站 Decision Tree for Optimization Software (plato.asu.edu/bench.html) 中,Gurobi 比其他大规模优化器有明显优势。