116. 填充每个节点的下一个右侧节点指针

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

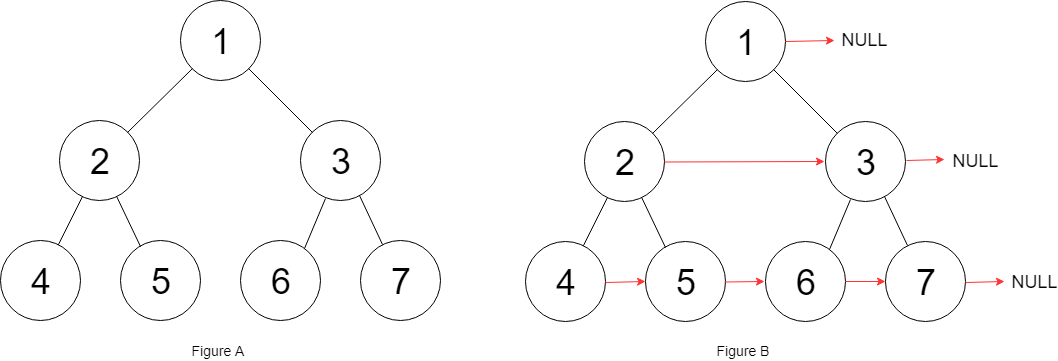
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

示例 2:

输入：root = []
输出：[]

提示：

• 树中节点的数量在 [0, 212 - 1] 范围内
• -1000 <= node.val <= 1000

我的答案：

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;

    Node() : val(0), left(NULL), right(NULL), next(NULL) {}

    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}

    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/

class Solution {
public:
    Node* connect(Node* root) {
        if (root == nullptr)
            return root;
        else {
            queue<Node*> Q;
            Q.push(root);
            while (!Q.empty()) {
                int size = Q.size();
                for (int i = 0; i < size; i++) {
                    Node* frist = Q.front();
                    Q.pop();
                    if (i < size - 1)
                        frist->next = Q.front();
                    if (frist->left)
                        Q.push(frist->left);
                    if (frist->right)
                        Q.push(frist->right);
                }
            }
        }
        return root;
    }
};

正确答案：

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;

    Node() : val(0), left(NULL), right(NULL), next(NULL) {}

    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}

    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/

class Solution {
    vector<Node*>pre;
public:
    Node* connect(Node* root) {
        dfs(root,0);
        return root;
    }
    void dfs(Node*node,int depth)
    {
        if(node==nullptr)
        return ;
        if(depth==pre.size())
        pre.push_back(node);
        else{
            pre[depth]->next=node;
            pre[depth]=node;
        }
        dfs(node->left,depth+1);
        dfs(node->right,depth+1);
    }
};

很巧妙，使用完美二叉树深度优先搜索每次递归回溯的都是最下面一层的节点，来将最后一层的结点串联起来，然后往上缩小层数。

我又retry了一下，这次我使用键值对:

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;

    Node() : val(0), left(NULL), right(NULL), next(NULL) {}

    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}

    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/

class Solution {
public:
    Node* connect(Node* root) {
        map<int,Node*> a;
        enter(root,0,a);
        return root;
        
    }
     void enter(Node*node,int depth,map<int,Node*>&a)
    {
        if(node==nullptr)
        return ;
        else
        {
            if(a.count(depth)>0)
            a[depth]->next=node;
            a[depth]=node;
            if(node->left)
            enter(node->left,depth+1,a);
            if(node->right)
            enter(node->right,depth+1,a);
        }
    }
};

我将深度作为键，节点作为值，每次遇到一个新的节点，我就首先将之前同一深度结点的最后一个链接这个新节点，这个新节点作为同一深度的最后一个结点。如果之前没有同一深度结点，那么这个节点就作为同一深度结点的最后一个节点。