作者简介：大家好，我是smart哥，前中兴通讯、美团架构师，现某互联网公司CTO

联系qq：184480602，加我进群，大家一起学习，一起进步，一起对抗互联网寒冬

学习必须往深处挖，挖的越深，基础越扎实！

阶段1、深入多线程

阶段2、深入多线程设计模式

阶段3、深入juc源码解析

阶段4、深入jdk其余源码解析

阶段5、深入jvm源码解析

码哥源码部分

码哥讲源码-原理源码篇【2024年最新大厂关于线程池使用的场景题】

码哥讲源码【炸雷啦！炸雷啦！黄光头他终于跑路啦！】

码哥讲源码-【jvm课程前置知识及c/c++调试环境搭建】

​​​​​​码哥讲源码-原理源码篇【揭秘join方法的唤醒本质上决定于jvm的底层析构函数】

码哥源码-原理源码篇【Doug Lea为什么要将成员变量赋值给局部变量后再操作？】

码哥讲源码【你水不是你的错,但是你胡说八道就是你不对了！】

码哥讲源码【谁再说Spring不支持多线程事务，你给我抽他！】

终结B站没人能讲清楚红黑树的历史，不服等你来踢馆！

打脸系列【020-3小时讲解MESI协议和volatile之间的关系，那些将x86下的验证结果当作最终结果的水货们请闭嘴】

引言

上篇文章介绍了算法的本质和基本概念《算法+数据结构（第01篇）走下神坛吧！算法》，这次我们用实际的问题来做算法实战。

假设如下场景：

公司新年晚会进行夺宝游戏，奖品是最新款的智能手机、VR游戏机、便携电脑三件套。

游戏规则如下：

当主持人宣布游戏开始的时候，每位员工的手机上会同时收到两组数字（数组中的每个数字都是正整数且两两不等）和一个目标正整数。

员工需要在两组数字中分别取两个数字相加，使得相加的结果与目标正整数最接近。哪位员工先做出结果，那么奖品就归谁。

为了使赢率最高，请问应该采用什么样的策略或者方法？

显然，这是在对一个特定问题找方法。那么根据上篇文章所讲到的，这就是在求算法。

那么如何算法求解呢？

答案就在上篇文章提到的“朴素而广泛的方法论”中。这个方法论其实就是算法求解的套路。

套路第一步：重新定义问题，结构化描述

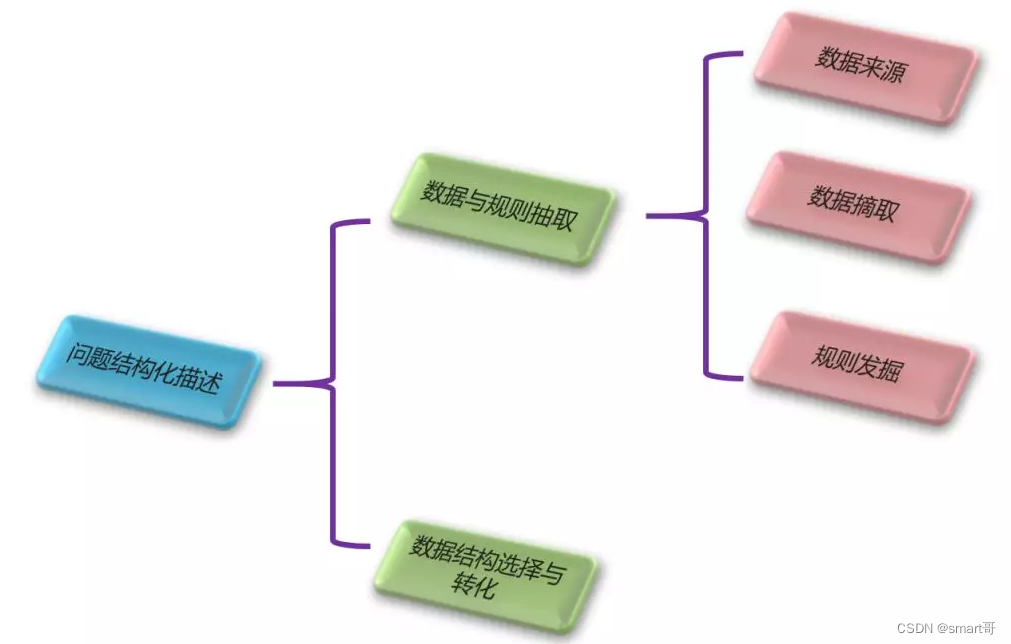
原问题是生活场景，要转换成结构化问题描述。结构化描述分为如下两步：数据与规则抽取、数据结构选择与转化。

数据与规则抽取

数据的来源： 数据一般在原问题描述中以名词、量词形式出现

数据的摘取：并不是所有的名词和量词都是有效数据。很明显，只有和问题求解相关的名词和量词才有意义。“问题求解”是动作，与动词相关。

那么是不是所有的动词都有效呢？也不是。只有和规则相关的动词才是有效的。

规则的发掘：规则就是抵达结果的条件。

根据上面的定义， 不难看出

数据是：两组数字（数组中的每个数字都是正整数且两两不等）、一个目标整数

规则是：从两组数字中分别取两个数字相加，相加的结果必须与目标正整数最接近

数据结构选择与转化

上篇文章已经讲到了：算法的依托是数据结构。如果把算法看做设计域的话，那么数据结构就是连接问题域到设计域的桥梁。那么如何选取合适的数据结构呢？

答案是：对上一步摘取的数据进行类型联想、关联。

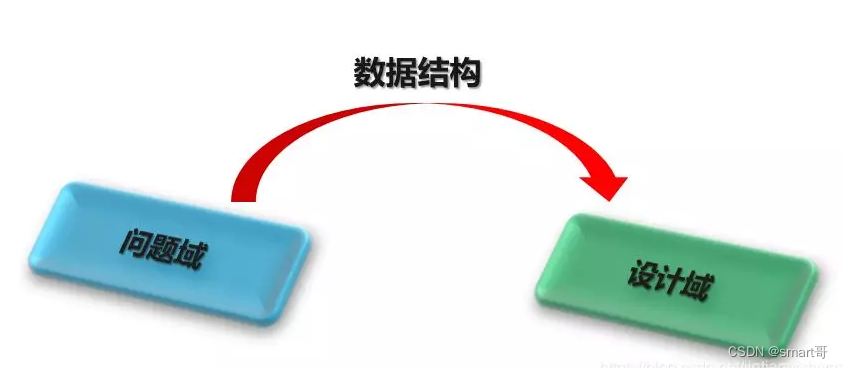
上一步中，我们已经摘取了数据——两组数和一个正整数。很明显，这里涉及到两个类型：数组和整数。

而这两个属于基础数据结构类型，至此数据结构选择问题解决了。接下来就是要对摘取的数据，基于选择的数据结构进行转化——“重整化”：

两组数字（数组中的每个数字都是正整数且两两不等）=> int A[]; int B[];

目标正整数 => int c;

聪明的你，一定会问一个问题：数据结构的选择仅仅就在这一步决定吗？

答案是否定的。数据结构的选择会贯穿整个算法设计，是一个不断迭代的过程。后面部分会详细阐述。

套路第二步：问题归类

算法问题的基本类型：搜索、排序、规划、计算。回到当前问题，根据问题描述，显然属于搜索类型。

套路第三步：经验匹配

现在我们来翻看已有的搜索算法，看看有没有能与当前问题匹配的。

理论上有3种情况：

第1种情况，100% 匹配，此时“直接拿来主义”；

第2种情况，部分匹配，此时可在已有算法基础上进行调整、组合或者改良；

第3种情况，完全不匹配，此时需要我们根据已有知识（甚至是跨学科知识，比方说数学、生物等），创新性地开发新算法。

针对搜索问题，我们有一个万能算法——“暴力搜索”，即遍历每一种可能性，直到找到答案。

但是这个算法要穷尽所有可能性，所以带来的时间和空间开销通常都是巨大的，用上篇文章的术语来讲，就是计算复杂度贼高。

为了给大家一个量化感觉，先用“暴力搜索”算法来解答这个题。

暴力搜索算法

对于数组A中的每一个元素进行遍历：

设当前元素为A[i]，则：

遍历数组b中的每一个元素B[j]：

(i)计算A[i]+B[j]的值，将所求的值记为t;

(ii) 计算t-c的绝对值|t-c|，记为k;

(iii) 如果当前的k比历史的k小（k的初值可以设成一个极大值）。

那么： 将 {A[i], B[j]}取代之前的候选结果，作为新的候选结果,待所有的遍历结束，最终的候选结果就是所要求的解。

上面的算法有两重循环，所以暴力搜索时间复杂度为O(La x Lb)。

其中La表示数组a中元素的个数，Lb表示数组b中元素的个数。

随着La和Lb的增大，复杂度以两者乘积速度上升。那么如何对暴力算法进行优化呢？

关于复杂度的计算，我会在下篇文章中详细介绍。

套路第四步：算法优化三步走

步骤1：

找到算法性能瓶颈源头，稍微分析一下，就明白：上述暴力搜索算法的开销在于穷尽了所有元素。

步骤2：

对源头进行改造，那么是否可以避免穷尽所有元素而得到结果呢？换言之，是否可以只比较部分元素、其他元素就自然被排除了呢？

要得到这样的效果，显然我们需要一种性质——这种性质必须是容易获得的：要么可以直接从当前数据中获取，要么可以通过已有方法（算法）获取。

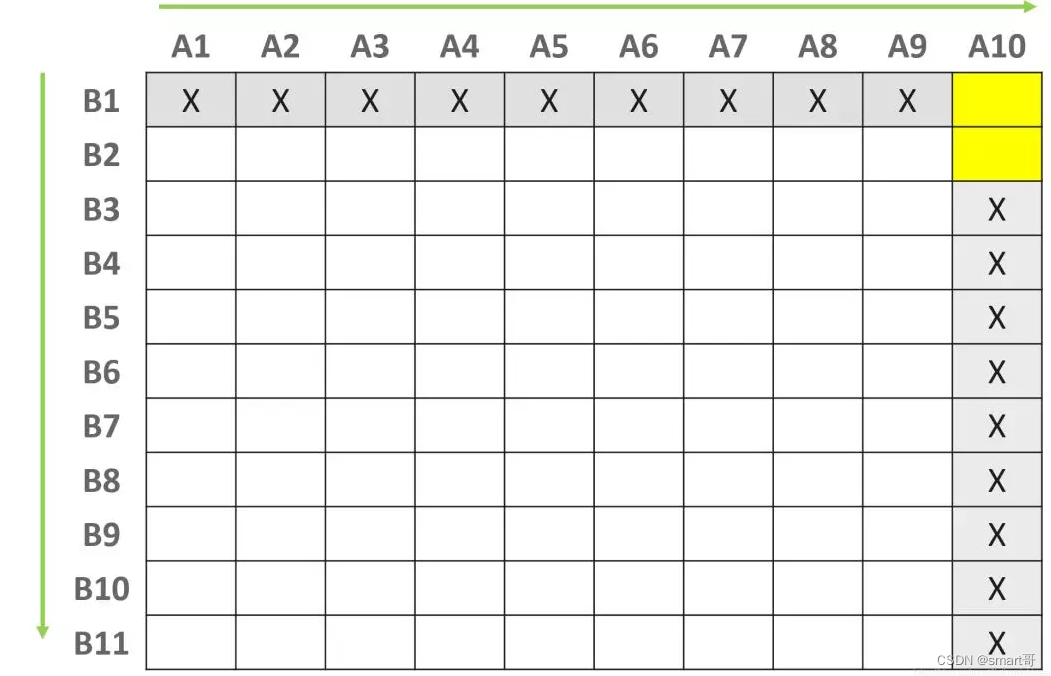
最容易想到的就是有序性，这种性质可以通过排序算法获取。我们可以用快速排序算法对A数组和B组数进行排序，将排序后的元素按照下图放置：

（为了方便表示，我们假设A数组是10个元素，B数组是12个元素）

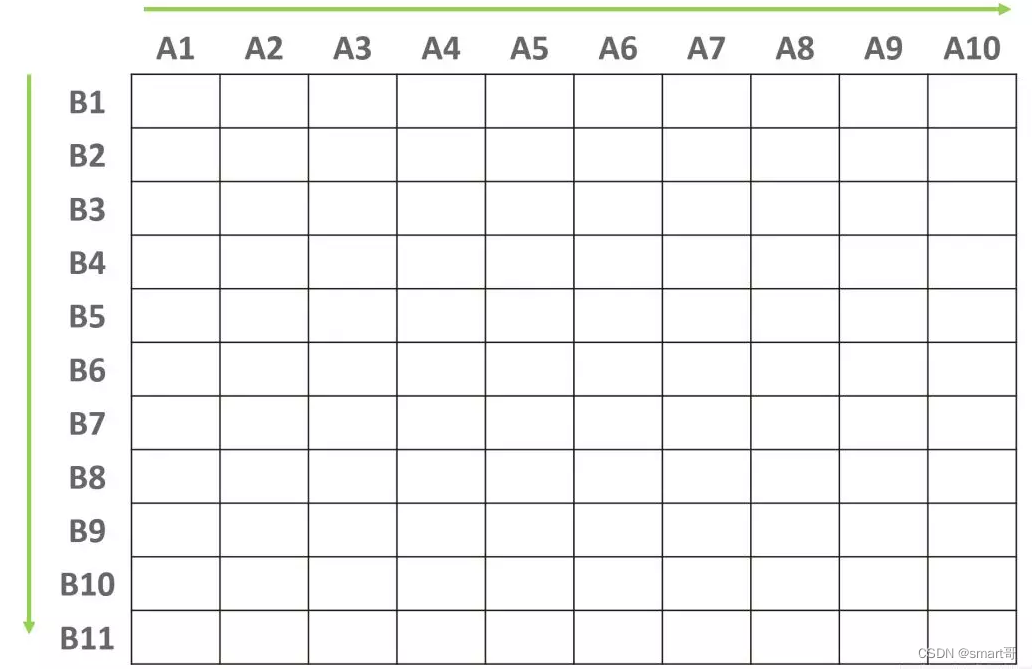
上图中的每个方格就是用来存放相加结果的。很显然，暴力搜索就是对上图中的每个方格都做了计算。

现在我们要做的，就是利用有序性，避开尽可能多的方格。

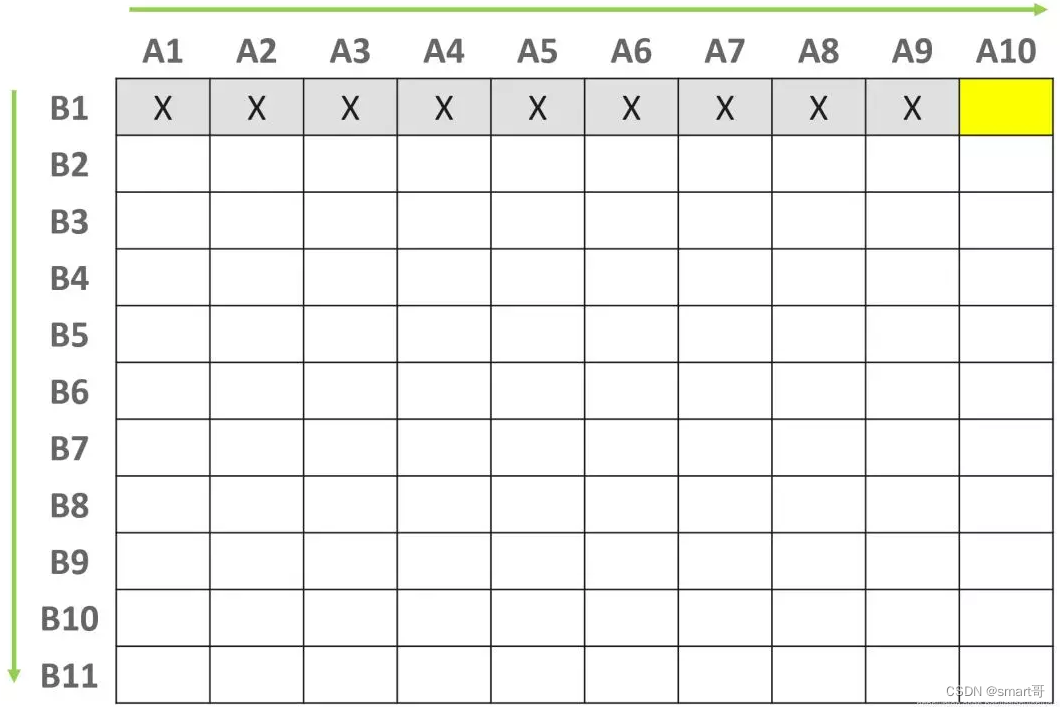
我们从右上角方格[A10, B1]开始遍历：

记s[A10, B1] = A10 + B1，则：

(i) 如果s[A10, B1] == 目标正整数c，那么元素对{A10， B1}即为所求解

(ii) 如果s[A10, B1] < 目标正整数c， 那么所有与[A10，B1]在同一排的方格都不用计算了

原因如下：因为A1<=A2<=...<=A9<=A10，所以s[A1, B1] <= s[A2, B1] <= ... <= s[A10, B1]，从而这些s距离c都比s[10, B1]远，都不是所求解。

(iii) 类似地，如果s[A10, B1] >目标正整数c，那么所有与A[10, B1]在同一列的方格都不用计算了,显然，按照对角线方向来遍历，每遍历一个方格，就可以避开一排或者一列的方格，感觉就像在玩扫雷游戏：）

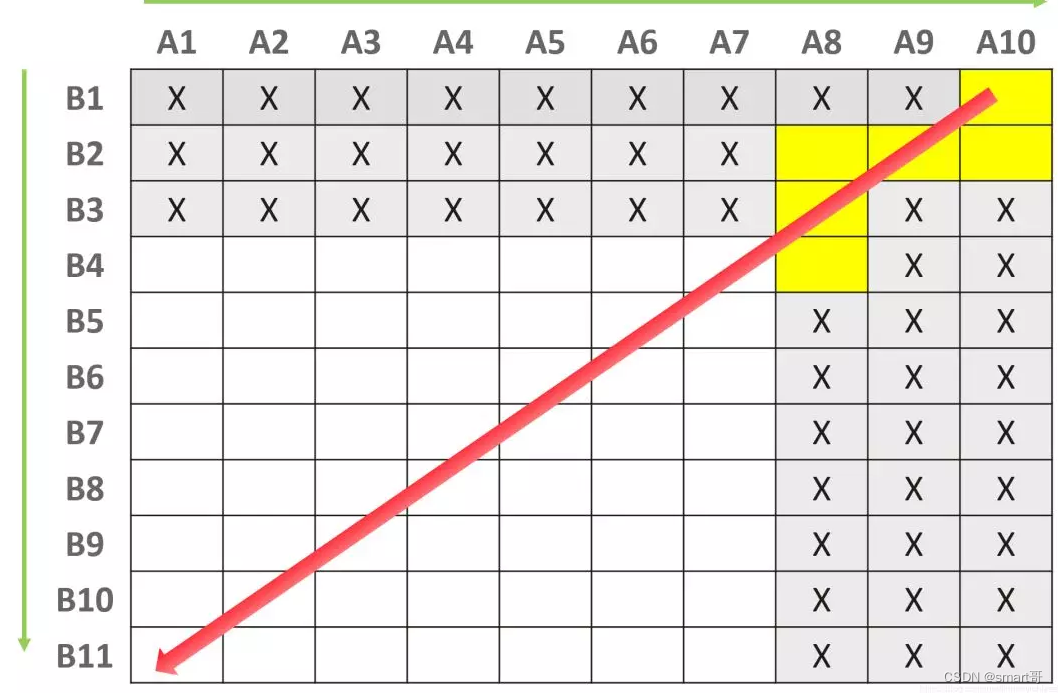
步骤3：验证

现在我们来验证一下优化后的算法的复杂度,整个算法分成两部分：

第1部分是快速排序。快速排序算法的时间复杂度是O(nlogn)，所以这部分的时间复杂度是 O(MAX(LalogLa, LblogLb))

第2部分是扫雷遍历。这部分最坏的情况就是走完整个对角线。此时共遍历La+Lb个方格，时间复杂度是O(La+Lb)

两者相加得到最坏情况下的整体时间复杂度为：O(MAX(LalogLa, LblogLb)+La+Lb)

好啦，就写到这里了，后续 连载 会持续更新…