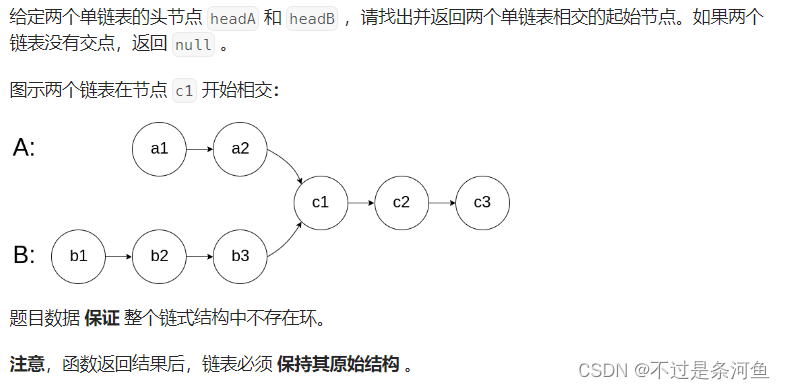
法一：蛮力法

        即顺序遍历第一个链表的每个节点，每遍历到一个节点，就在第二个链表中顺序遍历每个节点，比较是否有节点相同。该方法的时间复杂度是O（mn），空间复杂度是O（1）。

法二：入口节点

        首先遍历一个链表直至到达尾节点，将其next指针连接到该链表的头节点，那么就可以构造出一个包含环的链表，随后就转变为找出入口节点的问题。详情见链表中环的入口节点。该方法的时间复杂是O（m+n），空间复杂度是O（1）。

法三：栈

        由于重合节点只可能出现在链表的尾部，所以从两个链表的尾部开始向前比较，最后一个相同的节点就是所求节点。但单向链表只能从前向后遍历，而尾节点是要先比较的，这就是通常所说的“后进先出”，随即不难想到用栈。可以先把两个链表的节点分别放入两个辅助栈，接下来比较两个栈的栈顶节点是否相同，如果相同，则把栈顶节点弹出，然后比较下一个栈顶节点，最后一个相同的节点即为所求节点。该方法的时间复杂度是O（m+n），空间复杂度是O（m+n）。

法四：哈希表

        首先遍历第一个链表 ，并将链表中的每个节点加入一个哈希表中。然后顺序遍历另一个链表，对于遍历到的每个节点，判断该节点是否在哈希表中，第一个存在节点即为所求节点。该方法的时间复杂度是O（m+n），空间复杂度是O（m）。

法五：同步双指针

        之所以有法四是因为如果从头开始同时遍历两链表，两个指针到达第一个重合节点（如果有且两链表长度不一致）是不同步的。为了解决这个问题可以先遍历两个链表得到它们的长度，在第二次遍历时，初始化两指针分别指向链头，令较长的链表中的指针先移动若干步，然后两指针以相同速度在链表中移动，直到相遇。该方法的时间复杂度是O（m+n），空间复杂度是O（1）。

法六：循环双指针

        还是为了解决两链表因长度不同而带来的问题，仔细思考，如果两链表存在重合节点，那么从第一个重合节点开始到链表尾部都是相同的，也就是说长度不同是发生在重合之前。那么我们可以使用循环解决这个问题。首先初始化两个指针分别指向两个链表的头节点 。使用一个循环，每次迭代中，比较当前两个指针的节点是否相等，如果相等则找到了目标节点。如果不相等，则移动指针，如果到达链表末尾，则将其重新指向另一链表的头节点。这样，两个指针在链表上同时移动，如果存在交点，它们最终会在交点处相遇，如果没有交点，最终两个指针都会指向null。该方法的时间复杂度是O（m+n），空间复杂度是O（1）。

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    // 初始化两个指针，分别指向两个链表的头节点
    ListNode curA = headA;
    ListNode curB = headB;

    // 使用循环查找两个链表的交点
    while (curA != curB) {
        // 如果当前节点不为空，则移动到下一个节点，否则重新指向另一个链表的头节点
        curA = (curA != null) ? curA.next : headB;
        curB = (curB != null) ? curB.next : headA;
    }

    // 返回交点（如果存在），或者返回 null
    return curA;
}