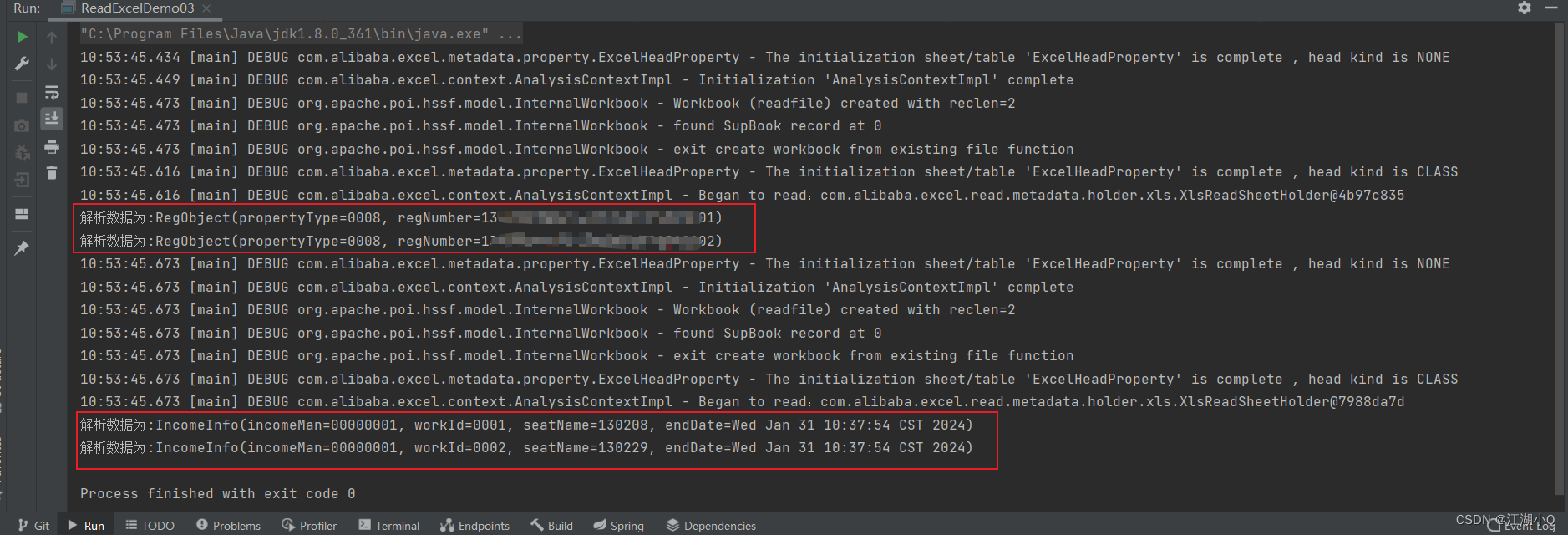
标题
- 代码详解
- Actor和Critic网络的设置
代码详解
代码链接(点击跳转)
Actor和Critic网络的设置
- 基本设置:3个智能体、每个智能体观测空间18维。
- Actor网络:实例化一个actor对象,input-size是18
- Critic网络:实例化一个Critic对象,input-size是18x3=54
- 在choose_action调用actor网络的时候,传入的直接是三个智能体的参数,tensor_size=[3,18];也就是说,智能体之间是共用一套参数的,也就是参数共享;(三个18维向量之间是相互独立的,改变其中一个向量的值,经过神经网络后,只有他自己的输出值改变了,而其他两个向量仍然是原来的大小);
- 在训练时,可以认为只有一个Critic网络,因此这叫做集中式训练;
- 值得注意的是,Critic网络的实际输入的向量的值是[3,54]!!而这三个向量是一模一样的。
- 关于reward,代码给出的实例是所有智能体共享同一奖励函数,因此将策略梯度算法扩展到多智能体场景下的最简单的方式就是每个智能体共用同一个全局 critic 函数。(但好像值分解的方法更合理一点)
2.box类
- box类对应于多维连续空间
- Box空间可以定义多维空间,每一个维度可以用一个最低值和最大值来约束
- 定义一个多维的Box空间需要知道每一个维度的最小最大值,当然也要知道维数。

作者在文献附录中有谈到说如果智能体是同种类的就采用相同的网络参数,对于每个智能体内部也可以采用各自的actor和critic网络,但是作者为了符号的便利性,直接就用的一个网络参数来表示)。