难度参考
难度:中等
分类:二叉树
难度与分类由我所参与的培训课程提供,但需要注意的是,难度与分类仅供参考。且所在课程未提供测试平台,故实现代码主要为自行测试的那种,以下内容均为个人笔记,旨在督促自己认真学习。
题目
给你二叉树的根节点root,返回其节点值的层序遍历。(即逐层地,从左到右访问所有节点)。
示例1:
输入:root=[3,9,20,null,null,15,7]
输出:[3],[9,20],[15,7]
提示:
树中节点数目在范围[0,20]内
-100<=Node.Val<=1000
思路
对于这个问题,我们可以使用广度优先搜索(BFS)算法来进行二叉树的层序遍历。BFS 通常使用队列来实现,通过不断出队和入队的方式,将每一层的节点依次遍历。
- 首先,我们需要定义一个队列(queue)来存储待遍历的节点。初始时,将根节点(root)入队。
- 然后,进入循环,直到队列为空。在每一次循环中,分别执行以下步骤:
- 从队列中取出当前节点,并将当前节点的值存入结果数组中(该层的结果数组)。
- 如果当前节点的左子节点不为空,将左子节点入队。
- 如果当前节点的右子节点不为空,将右子节点入队。
- 循环结束后,我们就能得到一个每层节点值的层序遍历结果数组。
最后,根据题目的要求,返回层序遍历的结果数组。
示例
假设我们有以下的二叉树:
3
/ \
9 20
/ \
15 7
我们可以按照层序遍历的顺序逐层访问节点。根据题目要求,层序遍历的结果数组应该是 [3], [9, 20], [15, 7]。
- 首先,将根节点 3 入队。
3 -------------------- / \ 3 9 20 -------------------- / \ 15 7 result = {} - 开始循环,第一层级只有根节点 3,所以当前队列中只有根节点 3。将根节点 3 出队,并将其值 3 放入当前层级结果数组中。然后,检查节点 3 的左右子节点,发现都不为空,将根节点的左子节点 9 入队,右子节点 20 入队。
3 -------------------- / \ 9, 20 9 20 -------------------- / \ 15 7 result = {3} - 进入下一层级循环。此时,队列中有两个节点,分别是节点 9 和节点 20。将节点 9 出队,并将其值 9 放入当前层级结果数组中。然后,检查节点 9 的左右子节点,发现都为空,所以不需要入队。接着,将节点 20 出队,并将其值 20 放入当前层级结果数组中。然后,将节点 20 的左子节点 15 入队,右子节点 7 入队。
3 -------------------- / \ 15, 7 9 20 -------------------- / \ 15 7 result = {3, 9, 20} - 再次进入下一层级循环。此时,队列中有两个节点,分别是节点 15 和节点 7。将节点 15 出队,并将其值 15 放入当前层级结果数组中。然后,检查节点 15 的左右子节点,发现都为空,所以不需要入队。接着,将节点 7 出队,并将其值 7 放入当前层级结果数组中。然后,检查节点 7 的左右子节点,发现都为空,所以不需要入队。
3 -------------------- / \ 9 20 -------------------- / \ 15 7 result = {3, 9, 20, 15, 7} - 循环结束,得到层序遍历的结果数组
[3], [9, 20], [15, 7]。
梳理
对于二叉树的层序遍历,使用队列是因为队列的先进先出(FIFO)特性能够确保每一层的节点按照从左到右的顺序被访问。
具体来说,层序遍历的思路是从根节点开始,依次将节点的左子节点和右子节点加入到队列中,然后从队列中取出节点进行访问。这样做可以保证每一层的节点按照从左到右的顺序进行访问,因为队列中先入队的节点会先出队。
通过使用队列,保证了层序遍历的节点访问顺序正确,能够按照层级逐步扩展,并且能够将每一层的节点按照顺序存储到结果数组中。
具体流程中,我们通过循环不断从队列中取出节点,并将其值存入结果数组中。然后,检查当前节点的左右子节点,如果存在则将其加入到队列中,以便后续的访问。
总结来说,队列在层序遍历中起到了承载节点的作用,能够确保每一层的节点按照顺序被访问。通过队列的先进先出特性,我们能够按照层级逐步扩展,从而得到二叉树的层序遍历结果。
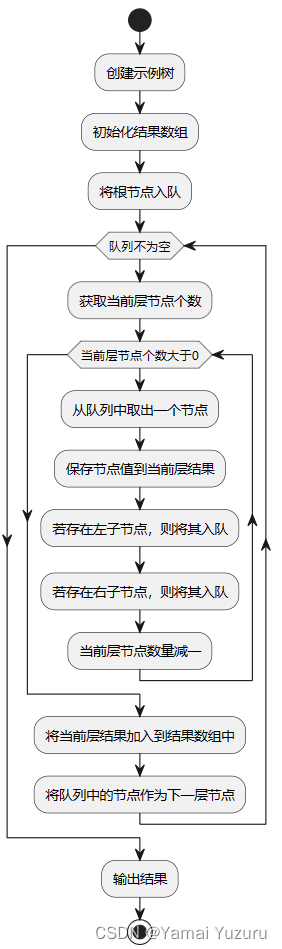
代码
#include <iostream> // 包含输入输出流库
#include <queue> // 包含队列库
#include <vector> // 包含向量库
using namespace std; // 使用标准命名空间
// 定义二叉树的节点
struct TreeNode {
int val; // 节点值
TreeNode* left; // 左子节点指针
TreeNode* right; // 右子节点指针
// 构造函数
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
// 层序遍历函数
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> result; // 存放最终层序遍历结果的向量
// 如果根节点为空,直接返回空结果
if (root == nullptr) {
return result;
}
// 创建队列,并将根节点入队
queue<TreeNode*> q;
q.push(root);
// 循环遍历队列,直到队列为空
while (!q.empty()) {
// 获取当前层的节点数量
int size = q.size();
vector<int> levelNodes; // 存放当前层节点值的向量
// 遍历当前层的节点
for (int i = 0; i < size; i++) {
// 弹出队列首节点,并将其值存入结果数组中
TreeNode* node = q.front();
q.pop();
levelNodes.push_back(node->val);
// 将当前节点的左子节点和右子节点入队
if (node->left) {
q.push(node->left);
}
if (node->right) {
q.push(node->right);
}
}
// 将当前层的节点值数组存入结果数组中
result.push_back(levelNodes);
}
// 返回结果数组
return result;
}
int main() {
// 创建示例树 [3, 9, 20, null, null, 15, 7]
TreeNode* root = new TreeNode(3);
root->left = new TreeNode(9);
root->right = new TreeNode(20);
root->right->left = new TreeNode(15);
root->right->right = new TreeNode(7);
// 执行层序遍历
vector<vector<int>> result = levelOrder(root);
// 输出结果
for (const auto& level : result) { // 遍历每一层
cout << "["; // 给输出结果添加左括号
for (const auto& val : level) { // 遍历当前层的节点值
cout << val << ","; // 输出节点值和逗号
}
cout << "]"; // 给输出结果添加右括号
}
return 0;
} 时间复杂度:O(n)
空间复杂度:O(n)
pop是队列的操作,用于移除队列中的队头元素(第一个元素)。push是队列的操作,用于将元素添加到队尾。push_back是向量的操作,用于将元素添加到向量的末尾。
在代码中,首先创建一个空的队列 q,然后使用 q.push(root) 将根节点 root 添加到队列中。接下来,通过循环遍历队列,每次从队列中取出一个节点,并将其值添加到 levelNodes 向量中。
同时,如果节点有左子节点或右子节点,通过 q.push 将它们添加到队列的尾部,以便在后续循环中处理它们。
最后,将 levelNodes 添加到 result 向量中,表示当前层的节点值。
整个过程将重复直到队列为空。最后返回 result 向量,即为二叉树的层序遍历结果。
在主函数中,示例了如何使用 levelOrder 函数来执行对创建的二叉树进行层序遍历,并将结果输出到屏幕上。
打卡