目录
一.递归:
1.1什么是递归?
1.2 递归示例:
①.打印问题:
②.阶乘问题:
1.3.递归需要遵守的规则:
二.迷宫问题:
说明:
代码详解:
三.八皇后问题:
思路:
代码解释:
一.递归:
1.1什么是递归?
递归(recursion):程序调用自身的一种编程方式
具体来说:
- 从调用层面:函数递归就是方法自己调用自己的一种方式,每次传入不同的变量
- 从编程技巧层面:一种方法(把一个大型复杂的程序转换为一个类似的小型简单的程序),这种方法的主要思想就是把大事化小
1.2 递归示例:
①.打印问题:
public class Method {
public static void test1(int n){
if(n>2){//退出递归的条件
test1(n-1);//向退出递归的条件逼近
}
System.out.println("n=" + n);//回溯时所要显示的信息,方便理解递归
}
public static void main(String[] args){
test1(4);//测试数据
}
}
每当执行一个方法的时候,就建立一个新的受保护的独立空间(栈空间),当一个方法执行完毕,或者遇到return,就返回,遵守谁调用,就将结果返回给谁。同时当方法执行完毕时或则返回时,该方法也就执行完毕。

②.阶乘问题:
public class Method {
public static int fun(int n){
if(n==0 || n==1){//退出递归条件
return 1;
}
return n*fun(n-1);//向退出递归的条件逼近
}
public static void main(String[] args){
int ret=fun(5);//测试数据
System.out.println("ret="+ret);//将最终结果输出
}
}这里通过方法不断调用自身,直到n*fun(n-1) --》fun(2)=2*fun(1) 时回溯依次得到fun(3)=3*fun(2),fun(4)=4*fun(3) ---》最终得出120
1.3.递归需要遵守的规则:
- 执行一个方法时,就创建一个新的受到保护的独立空间(栈空间)
- 方法的局部变量是独立的,不会相互影响
- 如果方法使用的是引用类型变量(比如数组),就会共享出引用类型的数据
- 递归必须向退出递归的条件逼近,否则就是无限递归,会出现StackOverflowError的错误当一个方法执行完毕,或者遇到return,就会返回,遵守谁调用,就将结果返回谁
二.迷宫问题:
说明:
给定一个迷宫,指明起点和终点,找出从起点出发到终点的有效可行路径,就是迷宫问题(maze problem)。
迷宫可以以二维数组来存储表示。0表示通路,1表示障碍。注意这里规定移动可以从上、下、左、右四方方向移动。我们接下来所用的迷宫如下,红色方块为障碍,白色为通路,要求从[1][1]走到[6][5]
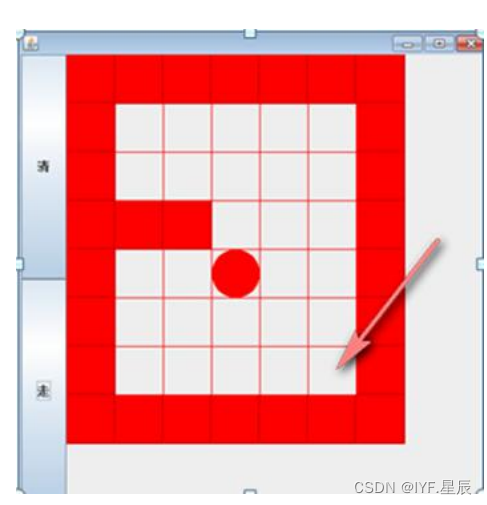
代码详解:
public class Method {
public static int getCount(int[][] map){//用于记录所走的步数的方法
int count=0;
for(int i=0;i<8;i++){
for(int j=0;j<7;j++){
if(map[i][j]==2){
count++;
}
}
}
return count;
}
/*使用递归回溯来给小球找路
//说明
//1. map 表示地图
//2. i,j 表示从地图的哪个位置开始出发 (1,1)
//3. 如果小球能到 map[6][5] 位置,则说明通路找到.
//4. 约定: 当map[i][j] 为 0 表示该点没有走过 当为 1 表示墙 ; 2 表示通路可以走 ; 3 表示该点已经走过,但是走不通
//5. 在走迷宫时,需要确定一个策略(方法) 下->右->上->左 , 如果该点走不通,再回溯
/**
*
* @param map 表示地图
* @param i 从哪个位置开始找
* @param j
* @return 如果找到通路,就返回true, 否则返回false
*/
public static boolean setWay(int[][] map, int i, int j) {//走迷宫的方法
if(map[6][5] == 2) { // 通路已经找到ok
return true;
} else {
if(map[i][j] == 0) { //如果当前这个点还没有走过
//按照策略 下->右->上->左 走
map[i][j] = 2; // 假定该点是可以走通.
if(setWay(map, i+1, j)) {//向下走
return true;
} else if (setWay(map, i, j+1)) { //向右走
return true;
} else if (setWay(map, i-1, j)) { //向上
return true;
} else if (setWay(map, i, j-1)){ // 向左走
return true;
} else {
//说明该点是走不通,是死路
map[i][j] = 3;
return false;
}
} else { // 如果map[i][j] != 0 , 可能是 1, 2, 3
return false;
}
}
}
public static void main(String[] args){
int[][] map=new int[8][7];//打印迷宫地图
for(int i=0;i<7;i++){
map[0][i]=1;
map[7][i]=1;
}
for(int i=0;i<8;i++){
map[i][0]=1;
map[i][6]=1;
}
map[3][1]=1;
map[3][2]=1;
System.out.println("迷宫地图");//输出打印好的迷宫地图
for(int i=0;i<8;i++){
for(int j=0;j<7;j++){
System.out.print(map[i][j]+" ");
}
System.out.println();
}
setWay(map,1,1);//走迷宫方法
System.out.println("走完后的地图");//输出走完后的地图
for(int i=0;i<8;i++){
for(int j=0;j<7;j++){
System.out.print(map[i][j]+" ");
}
System.out.println();
}
int count=getCount(map);
System.out.println("走迷宫所用的步数为:"+count);
}
}输出结果:其中1为墙,0为通路,2为走过的且能走通的路,3为死路

三.八皇后问题:
说明:
八皇后问题,是一个古老而著名的问题,是回溯算法的典型例题。该问题是十九世纪著名的数学家高斯1850年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法并输出每一种摆法。

思路:
- 第一个皇后先放第一行第一列
- 第二个皇后放在第二行第一列,然后判断是否OK,如果不OK,继续放在第二列,第三列,依次把所有 列都放完,找到一个合适的
- 继续第三个皇后,还是第一列,第二列,……直到第8个皇后也能放在一个不冲突的位置,算是找到了一个正确的解
- 每得到一个正确解时,在栈回退到上一个栈是,就会开始回溯,即将第一个皇后,放到第一列的所有正确解,全部得到
- 然后回头继续第一个皇后放第二列,后面循环1,2,3,4步骤
代码解释:
public class Queue8 {
//定义一个max表示共有多少个皇后
int max = 8;
//定义数组array, 保存皇后放置位置的结果,比如 arr = {0 , 4, 7, 5, 2, 6, 1, 3}
int[] array = new int[max];
static int count = 0;
static int judgeCount = 0;
public static void main(String[] args) {
//测试一把 , 8皇后是否正确
Queue8 queue8 = new Queue8();
queue8.check(0);
System.out.printf("一共有%d解法", count);
System.out.printf("一共判断冲突的次数%d次", judgeCount); // 1.5w
}
//编写一个方法,放置第n个皇后
//特别注意: check 是 每一次递归时,进入到check中都有 for(int i = 0; i < max; i++),因此会有回溯
private void check(int n) {
if(n == max) { //n = 8 , 其实8个皇后就既然放好
print();
return;
}
//依次放入皇后,并判断是否冲突
for(int i = 0; i < max; i++) {
//先把当前这个皇后 n , 放到该行的第1列
array[n] = i;
//判断当放置第n个皇后到i列时,是否冲突
if(judge(n)) { // 不冲突
//接着放n+1个皇后,即开始递归
check(n+1); //
}
//如果冲突,就继续执行 array[n] = i; 即将第n个皇后,放置在本行得 后移的一个位置
}
}
//查看当我们放置第n个皇后, 就去检测该皇后是否和前面已经摆放的皇后冲突
/**
*
* @param n 表示第n个皇后
* @return
*/
private boolean judge(int n) {
judgeCount++;
for(int i = 0; i < n; i++) {
// 说明
//1. array[i] == array[n] 表示判断 第n个皇后是否和前面的n-1个皇后在同一列
//2. Math.abs(n-i) == Math.abs(array[n] - array[i]) 表示判断第n个皇后是否和第i皇后是否在同一斜线
// n = 1 放置第 2列 1 n = 1 array[1] = 1
// Math.abs(1-0) == 1 Math.abs(array[n] - array[i]) = Math.abs(1-0) = 1
//3. 判断是否在同一行, 没有必要,n 每次都在递增
if(array[i] == array[n] || Math.abs(n-i) == Math.abs(array[n] - array[i]) ) {
return false;
}
}
return true;
}
//写一个方法,可以将皇后摆放的位置输出
private void print() {
count++;
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
}
打印解法过程太长,这里就截取了解法个数和冲突次数
博客到这里也是结束了,制作不易,喜欢的小伙伴可以点赞加关注支持下博主,这对我真的很重要~~



![BUUCTF-Real-[ThinkPHP]5-Rce](https://img-blog.csdnimg.cn/direct/da9ea0965ec243f3bf9b24fb1505bade.png)